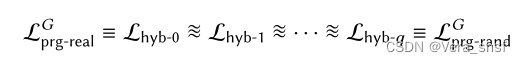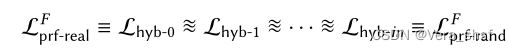【Joy of Cryptography 读书笔记】Chapter 6 伪随机函数（Pseudorandom Function）&分组密码（Block Cipher）

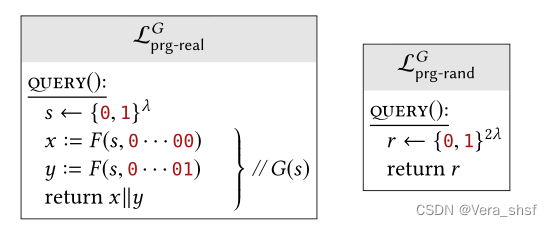
伪随机函数（pseudorandom function ，PRF）也是密码学中的一个重要工具，它是一个确定性的函数 F : { 0 , 1 } λ × { 0 , 1 } i n → { 0 , 1 } o u t F:\{0,1\}^\lambda\times\{0,1\}^{in}\rightarrow\{0,1\}^{out} F:{0,1}λ×{0,1}in→{0,1}out，其中输入为密钥空间 × \times ×输入空间。一个PRF是安全的，是希望对于每一个输入，其输出结果像是在 { 0 , 1 } o u t \{0,1\}^{out} {0,1}out中随机选取（均匀采样）的。下面给出安全PRF的形式化定义。

定义6.1 对于一个确定性函数 F : { 0 , 1 } λ × { 0 , 1 } i n → { 0 , 1 } o u t F:\{0,1\}^\lambda\times\{0,1\}^{in}\rightarrow\{0,1\}^{out} F:{0,1}λ×{0,1}in→{0,1}out， F F F是一个安全的PRF当且仅当如下图定义的两个库不可区分（即 L p r f − r e a l F ≈ ~ L p r f − r a n d F L_{prf-real}^F\widetilde\approx L_{prf-rand}^F Lprf−realF​≈ Lprf−randF​）：

其中右边的随机库中的 T T T可以理解为一个函数表格，而对于每一个输入 x x x，都是在 { 0 , 1 } o u t \{0,1\}^{out} {0,1}out中均匀采样。只不过上图的 T T T没有一开始就直接把所有 x x x对应的 y y y都确定了，而是按需确定——这样的做法在实际中可以减少不必要的开销（毕竟所有的输入规模高达 2 i n 2^{in} 2in，如果 i n ≥ λ in\ge\lambda in≥λ这将是指数级别），而且整个过程与提前确定的效果没有区别（都是均匀采样）。

值得注意的是，伪随机函数中**“随机函数”是指该函数是在一组函数中被随机选择出来的**。在随机库中的 T T T可以视为一个 { 0 , 1 } i n → { 0 , 1 } o u t \{0,1\}^{in}\rightarrow\{0,1\}^{out} {0,1}in→{0,1}out的函数，那么随机库中正是在所有这样的函数中随机选择了一个。而PRF则是通过密钥 k k k随机选取了一个函数，它的效果需要和随机库的不可区分。这里并不能理解为函数 T T T是一个带有随机性的函数，这也可以根据库的定义得知（ F F F也是确定的函数，因为 k k k是内置选定的）——也就是调用两次随机库/PRF，相同的输入 x x x所得的输出是相同的。

上一章已经介绍过密码学的一个重要工具PRG（伪随机数生成器）。实际应用中，通常使用PRF构造PRG；也可以用PRG构造PRF，但一般是在理论上，实际上并不这样构造。下面将分别介绍上述两种情况的一种构造。

假设有一个安全的PRG F : { 0 , 1 } λ × { 0 , 1 } λ → { 0 , 1 } λ F:\{0,1\}^\lambda\times\{0,1\}^\lambda\rightarrow\{0,1\}^\lambda F:{0,1}λ×{0,1}λ→{0,1}λ（即 i n = o u t = λ in=out=\lambda in=out=λ），那么可以用如下方法构造一个length-doubling PRG：

上述构造也称为Counter PRG，因为它可以通过扩展 F F F的输入（比如增加0…10，0…11）来构成更长的输出，就像计数器（counter）一样。而这个PRG的安全性是由均匀采样所得的密钥 s s s来保证的。下面将对其安全性进行证明。

定理6.1 如果 F F F是一个安全的PRF，那么如上图所构造的Counter PRG G ( s ) G(s) G(s)是一个安全的PRG。

证明：根据PRG的安全性定义（定义5.1），我们需要证明如下两个库是不可区分的：

而我们已知的是 F F F具备如定义6.1所示的安全性（下图只是方便阅读，和之前的图一样）：

我们依然使用Hybrid方法去证明。但是值得注意的是， L p r f − r e a l F L_{prf-real}^F Lprf−realF​的密钥 k k k在每次调用时不变的，而 L p r g − r e a l G L_{prg-real}^G Lprg−realG​中的 s s s每次调用并不相同，因此无法直接将 L p r g − r e a l G L_{prg-real}^G Lprg−realG​等价于 L p r f − r e a l F L_{prf-real}^F Lprf−realF​。也就是说， L p r f − r e a l F L_{prf-real}^F Lprf−realF​的使用只能对应一次 s s s加密的情况。但是这也带给我们启示： s s s的取值其实是和第几次调用QUERY有关，因为在一次调用内， s s s取值是相同的。为此，这里的Hybrid证明的中间库将不向以前一样 个数是明确的，而是取决于调用QUERY的次数（变量） q q q——这样的证明称为Variable-Hybrid Proof。

在个人理解里，Variable-Hybrid证明中用到的思路有些数学归纳法的影子。它希望证明的是如下式子（ L h y b − i L_{hyb-i} Lhyb−i​是中间库）：

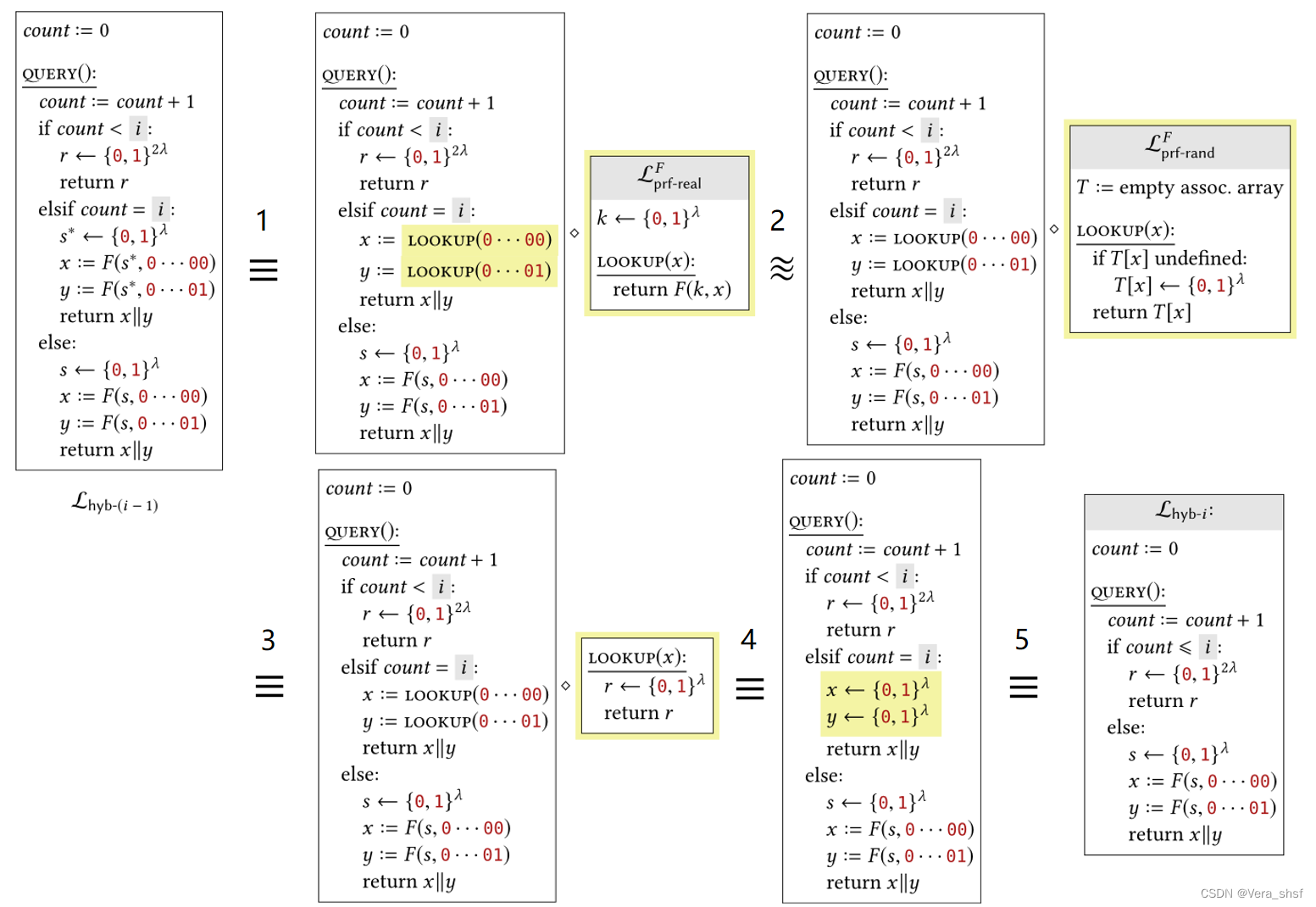
因此它的思路是：构造一个带变量的库 L h y b − i L_{hyb-i} Lhyb−i​，首先证明 L p r g − r e a l G ≡ L h y b − 0 L_{prg-real}^G\equiv L_{hyb-0} Lprg−realG​≡Lhyb−0​、 L p r g − r a n d G ≡ L h y b − q L_{prg-rand}^G\equiv L_{hyb-q} Lprg−randG​≡Lhyb−q​；然后证明 L h y b − ( i − 1 ) ≈ ~ L h y b − i L_{hyb-(i-1)}\widetilde\approx L_{hyb-i} Lhyb−(i−1)​≈ Lhyb−i​，利用不可区分的传递性得到结果。那么在本次 L h y b − i L_{hyb-i} Lhyb−i​的构造中，也应该充分利用证明思路中的特点： i i i是从0开始依次递增证明的，相当于对于调用次数 q q q而言也是从小到大逐步证明调用 q q q次是安全的，所以在 q + 1 q+1 q+1次的时候可以利用前 q q q次调用是安全的结论——这也是个人感觉有点像归纳法的原因。在本次证明中，构造的 L h y b − i L_{hyb-i} Lhyb−i​如下图所示：

首先对于 i = 0 i=0 i=0，可以得知必然走else分支，因此 L p r g − r e a l G ≡ L h y b − 0 L_{prg-real}^G\equiv L_{hyb-0} Lprg−realG​≡Lhyb−0​。对于 i = q i=q i=q，将执行if分支，因此 L p r g − r a n d G ≡ L h y b − q L_{prg-rand}^G\equiv L_{hyb-q} Lprg−randG​≡Lhyb−q​。接下来只需证明 L h y b − ( i − 1 ) ≈ ~ L h y b − i L_{hyb-(i-1)}\widetilde\approx L_{hyb-i} Lhyb−(i−1)​≈ Lhyb−i​。观察上图可知， L h y b − ( i − 1 ) L_{hyb-(i-1)} Lhyb−(i−1)​和 L h y b − i L_{hyb-i} Lhyb−i​的区别就是 c o u n t = i count=i count=i的这一次执行，如果可以证明这一次与在 { 0 , 1 } 2 λ \{0,1\}^{2\lambda} {0,1}2λ上均匀采样不可区分，就完成证明。而针对一次 s s s的取值，就可以使用PRF的安全性了。具体证明过程如下：

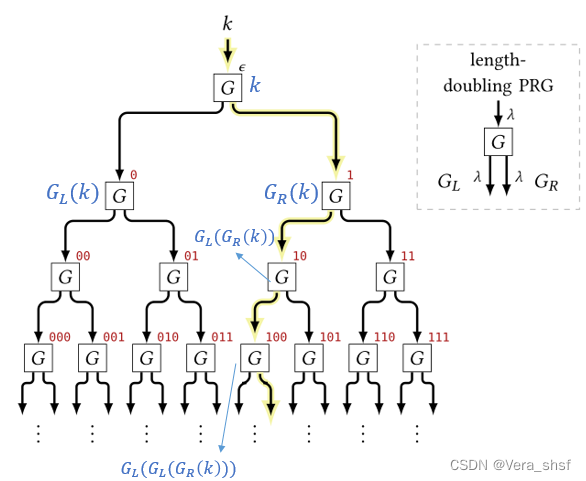
上述步骤1中将 c o u n t = i count=i count=i这次的执行转换为PRF，然后步骤2中使用了PRF的安全性。由于对 L p r f − r a n d F L_{prf-rand}^F Lprf−randF​的两次调用， x x x都是不同的（分别是0…00和0…01），因此都执行if分支，因此在步骤3可以简化为直接均匀采样。步骤4、5则是内联。至此，完成了Counter PRG的安全性证明。

这里介绍的构造方法是一种理论上的构造方法（效率不高，因此实际中未采用，但有理论价值）。假设有一个length-doubling PRG G : { 0 , 1 } λ → { 0 , 1 } 2 λ G:\{0,1\}^\lambda\rightarrow\{0,1\}^{2\lambda} G:{0,1}λ→{0,1}2λ，可以根据如下的树型（完全二叉树）构造得到一个PRF F : { 0 , 1 } λ × { 0 , 1 } i n → { 0 , 1 } λ F:\{0,1\}^\lambda\times \{0,1\}^{in}\rightarrow\{0,1\}^\lambda F:{0,1}λ×{0,1}in→{0,1}λ。

这个PRF是这样工作的：首先将密钥 k k k作为根节点PRG的输入得到 G ( k ) G(k) G(k)，然后根据输入 x x x的第一位是0（1）而保留前（后） λ \lambda λ位 G L G_{L} GL​（ G R G_R GR​），作为下一个节点PRG的输入。后面的以此类推（上图中蓝色的部分标注了部分节点的输入，也就是每个节点的值）。由此可知，树高就是 i n + 1 in+1 in+1（根节点为第一层），而对于不同的输入 x x x相当于从根节点出发走了一条路径抵达叶节点（比如标黄的输入就是100…），而叶节点的值就是最终输出。

上述构造（称为GCM PRF）可以进行如下形式化定义：

下面将证明该PRG的安全性。

定理6.2 对于如上图定义的GCM PRF，如果 G G G是一个安全的length-doubling PRG，那么 F F F是一个安全的PRF。

证明：根据PRF的安全性定义（定义6.1，下图只是方便查看），我们需要证明如下两个库不可区分，其中 F F F如上图定义。

我们依然使用Variable-Hybrid证明方法，而这次的变量是输入的长度 i n in in。证明的思路与上一小节类似，即证明：

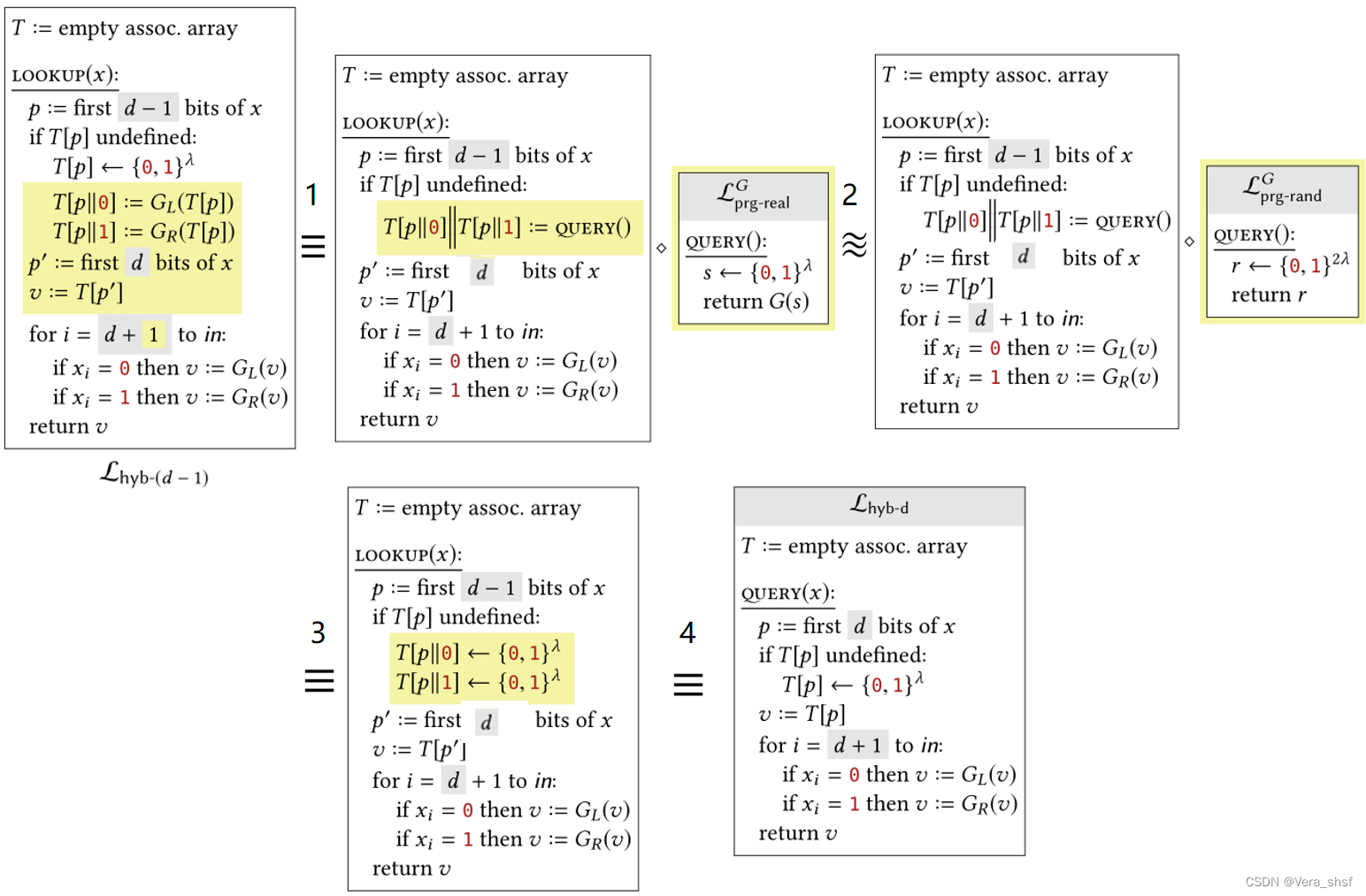
类似的思路（对in递归的想法）构造如下中间库：

首先对于 d = 0 d=0 d=0时， p = ϵ p=\epsilon p=ϵ，首次调用时将执行if分支，因此相当于随机选取了 k k k（之后便固定了），后面循环与 F F F的定义一致，故有 L p r f − r e a l F ≡ L h y b − 0 L_{prf-real}^F\equiv L_{hyb-0} Lprf−realF​≡Lhyb−0​。对于 d = i n d=in d=in， p = x p=x p=x，而不执行for循环，而for循环之前的代码与 L p r f − r a n d F L_{prf-rand}^F Lprf−randF​的一致，故有 L p r f − r a n d F ≡ L h y b − i n L_{prf-rand}^F\equiv L_{hyb-in} Lprf−randF​≡Lhyb−in​。

接下来只需证明 L h y b − ( d − 1 ) ≈ ~ L h y b − d L_{hyb-(d-1)}\widetilde\approx L_{hyb-d} Lhyb−(d−1)​≈ Lhyb−d​。类似地可以发现两者之差就是在于 L h y b − ( d − 1 ) L_{hyb-(d-1)} Lhyb−(d−1)​在 i n > d − 1 in>d-1 in>d−1时会多执行一次循环。因此如果想要让其形式转化为 L h y b − d L_{hyb-d} Lhyb−d​，可以将这一次的循环拆解出来，并利用PRG的安全性证明它与均匀采样不可区分。完整的证明过程如下：

步骤1左侧是 L h y b − ( d − 1 ) L_{hyb-(d-1)} Lhyb−(d−1)​将 i = d i=d i=d这一次循环拆解出来后的形式。虽然在原来的循环中只会计算一个子节点的值（只执行其中一个if），但是多计算（因为 G G G是个确定性函数，所以整个树是确定的，只是不一定每个节点都计算出来了）并不影响。由于然后步骤1将undefined分支的内容写成调用PRG。步骤2则使用PRG的安全性定义。步骤3中，由于两者拼接起来是个均匀采样，因此每一部分也是均匀采样的。步骤4左侧与右侧相比，就是多计算了一个子节点，同理因为树是确定的，这不影响。至此，证毕。

这里书上的图在1-3步骤等号右侧的库中 p ′ p' p′全部是 f i r s t first first d + 1 d+1 d+1 bits，不知是否是有误。因为根据描述应该这一行没有做变换。

现在我们考虑PRF的一种特殊的情况。假设这个PRF的输入和输出长度相同（ i n = o u t in=out in=out），而且对于每一个密钥 k k k都是可逆的（invertible）。可逆是希望在知道密钥的条件下可以解密。具有这样特殊性质的PRF被称为伪随机置换（pseudorandom permutation ，PRP）或分组密码（block cipher，也称为块密码）。之所以称之为**“置换”，是因为满足可逆意味着这个函数是单射，而输入空间和输出空间相同则意味着满射，因此是双射函数**——这既是PRP的性质所要求的，也是置换的（集合论）数学定义。而**“随机置换”的含义和PRF中“随机函数”的含义是类似的，也就是在所有从输入空间到输出空间的置换中随机选择一个**。下面给出安全PRP的形式化定义。

定义6.2 对于一个确定性函数 F : { 0 , 1 } λ × { 0 , 1 } b l e n → { 0 , 1 } b l e n F:\{0,1\}^\lambda\times\{0,1\}^{blen}\rightarrow\{0,1\}^{blen} F:{0,1}λ×{0,1}blen→{0,1}blen（ b l e n blen blen称为分组长度， { 0 , 1 } b l e n \{0,1\}^{blen} {0,1}blen中任意一个元素称为一个分组），满足对于任意给定的密钥 k ∈ { 0 , 1 } λ k\in \{0,1\}^\lambda k∈{0,1}λ，存在逆函数 F − 1 : { 0 , 1 } λ × { 0 , 1 } b l e n → { 0 , 1 } b l e n F^{-1}:\{0,1\}^\lambda\times\{0,1\}^{blen}\rightarrow\{0,1\}^{blen} F−1:{0,1}λ×{0,1}blen→{0,1}blen，对任意输入 x ∈ { 0 , 1 } b l e n x\in\{0,1\}^{blen} x∈{0,1}blen都有 F − 1 ( k , F ( k , x ) ) = x F^{-1}(k,F(k,x))=x F−1(k,F(k,x))=x。 F F F是一个安全的PRP当且仅当如下图定义的两个库不可区分（即 L p r p − r e a l F ≈ ~ L p r p − r a n d F L_{prp-real}^F\widetilde\approx L_{prp-rand}^F Lprp−realF​≈ Lprp−randF​）：

上图中标黄的部分是与PRF安全定义中不同的部分（real是一样的），这是因为PRP要求单射，所以需要不重复的均匀采样。

从上面的安全性定义可以知道，PRP的安全性只是要求 F F F是安全的，并没有对其逆函数做任何要求。如果其逆函数 F − 1 F^{-1} F−1也要求是安全的，这就引入强伪随机置换的概念：

定义6.3 对于一个确定性函数 F : { 0 , 1 } λ × { 0 , 1 } b l e n → { 0 , 1 } b l e n F:\{0,1\}^\lambda\times\{0,1\}^{blen}\rightarrow\{0,1\}^{blen} F:{0,1}λ×{0,1}blen→{0,1}blen。 F F F是一个安全的强伪随机置换（strong pseudorandom permutation，SPRP）当且仅当如下图定义的两个库不可区分（即 L s p r p − r e a l F ≈ ~ L s p r p − r a n d F L_{sprp-real}^F\widetilde\approx L_{sprp-rand}^F Lsprp−realF​≈ Lsprp−randF​）：

从上一节可以看到PRF和PRP有所联系，因此本节将讨论它们的关系。

对比定义6.1和定义6.2（除去安全性的部分），可以发现定义上PRP就是PRF。但是一个安全的PRP未必是一个安全的PRF。而书上提到一种想法：如果PRP的输入空间特别大（比如 b l e n = λ blen=\lambda blen=λ），那么多项式级别的查询只是很少一部分，那么将不可区分。个人是这样理解如何提出这样一种想法的：可以看到在两者安全性定义不同的部分正是均匀采样和不重复选择这两个库的差别，而定理4.4已经给出了这两个库的advantage（可以理解为区分概率，实际上是两者调用结果相同的概率之差）紧确界为 Θ ( q 2 2 λ ) \Theta(\frac{q^2}{2^\lambda}) Θ(2λq2​)，其中的 2 λ 2^\lambda 2λ是输入规模， q q q是采样次数（因为当时是用生日概率证明的）。因此要想两者不可区分，输入规模必须是超多项式的（比如 b l e n = λ blen=\lambda blen=λ），故有如下的转换引理。

定理6.3（PRP转换引理） 对于如定义6.1、定义6.2所定义的 L p r f − r a n d L_{prf-rand} Lprf−rand​、 L p r p − r a n d L_{prp-rand} Lprp−rand​，当 i n = o u t = b l e n = λ in=out=blen=\lambda in=out=blen=λ时，有 L p r f − r a n d ≈ ~ L p r p − r a n d L_{prf-rand}\widetilde\approx L_{prp-rand} Lprf−rand​≈ Lprp−rand​。

定理6.3是本书给出的PRP转换引理的版本，其含义（或者说推论）就是对于一个 b l e n = λ blen=\lambda blen=λ的PRP，如果它是安全的，那么它也是一个安全的PRF。在其他资料上还有其他描述，比如输入是超多项式，或者 ∣ A d v P R P ( A ) − A d v P R F ( A ) ∣ ≤ q ( q − 1 ) 2 n + 1 |Adv_{PRP}(A)−Adv_{PRF}(A)|≤\frac{q(q−1)}{2^{n+1}} ∣AdvPRP​(A)−AdvPRF​(A)∣≤2n+1q(q−1)​。个人认为其实都是用了定理4.4中两个库的advantage的确界的结论。

证明：其实用到的就是定理4.4中的不可区分库：均匀采样和不重复选（如下图左、右）。值得注意的是，定理4.4成立对输入规模是有条件的，才能使得advantage可忽略。此时advantage紧确界为 Θ ( q 2 2 b l e n ) \Theta(\frac{q^2}{2^{blen}}) Θ(2blenq2​)，由于 b l e n = λ blen=\lambda blen=λ，因此advantage可忽略。

将 L p r f − r a n d L_{prf-rand} Lprf−rand​、 L p r p − r a n d L_{prp-rand} Lprp−rand​相同的部分定义为 L ∗ L^* L∗：

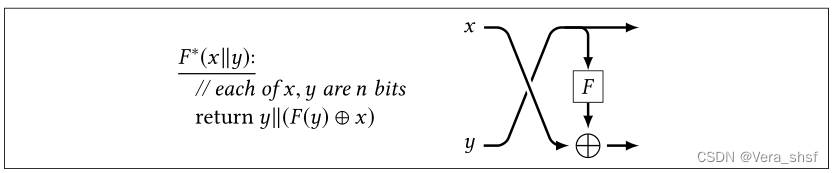
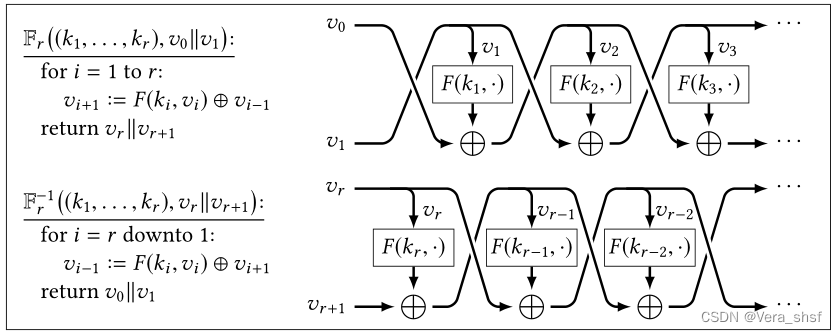
使用定理4.4，易得 L p r f − r a n d ≡ L ∗ ⋄ L s a m p − L ≈ ~ L ∗ ⋄ L s a m p − R ≡ L p r p − r a n d L_{prf-rand}\equiv L^*\diamond L_{samp-L}\widetilde\approx L^*\diamond L_{samp-R}\equiv L_{prp-rand} Lprf−rand​≡L∗⋄Lsamp−L​≈ L∗⋄Lsamp−R​≡Lprp−rand​。

这个引理的证明过程（定理4.4成立的条件）也说明了只有在输入规模足够大的时候，一个安全的PRP才是安全的PRF。

Feistel提出了一种用PRF构造PRP的方法，其主要思路就是利用不一定可逆的函数 F : { 0 , 1 } n → { 0 , 1 } n F:\{0,1\}^n\rightarrow\{0,1\}^n F:{0,1}n→{0,1}n去构造一个可逆的函数 F ∗ : { 0 , 1 } 2 n → { 0 , 1 } 2 n F^*:\{0,1\}^{2n}\rightarrow\{0,1\}^{2n} F∗:{0,1}2n→{0,1}2n。构造如下图所示，这个结构也称为Feistel轮（Feistel round），其中的 F F F也被称为轮函数（round function）。

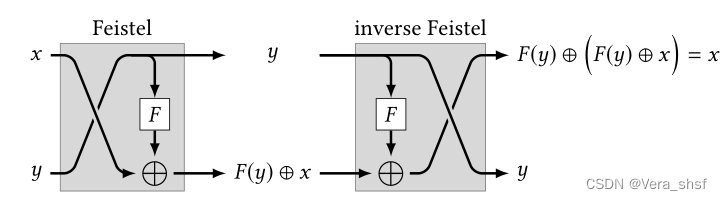
无论轮函数 F F F是什么，函数 F ∗ F^* F∗是可逆的，而且它的逆函数如从下图右侧所示（inverse Feistel）。这个逆函数的构造思路也十分简单，就是在得到 y , F ( y ) ⊕ x y,F(y)\oplus x y,F(y)⊕x后如何恢复成 x , y x,y x,y即可。

正如前文所说，轮函数 F F F并没有太多的限制，因此它也可以是一个带有密钥的函数，此时的 F ∗ F^* F∗被称为带有密钥的Feistel轮（keyed Feistel）。

现在回到用PRF构造PRP，上面的结构已经构造了一个可逆函数，那么是否只要 F F F是一个安全的PRF， F ∗ F^* F∗就是一个安全的PRP呢？答案是否定的，因为 F ∗ F^* F∗的输出中包含了一半的输入，这显然不能满足PRP的安全性（定义6.2）——因为对于每一个输入的输出都应该是像是均匀采样，但是如果按照 F ∗ F^* F∗中输入的 y y y相同那么输出的前半部分一定相同，这样无法和均匀采样出来的不可区分（advantage为 1 − 1 2 n 1-\frac{1}{2^n} 1−2n1​）。

为了避免上述的不安全性，Feistel密码（Feistel cipher）是采用如下图所示的构造方式：

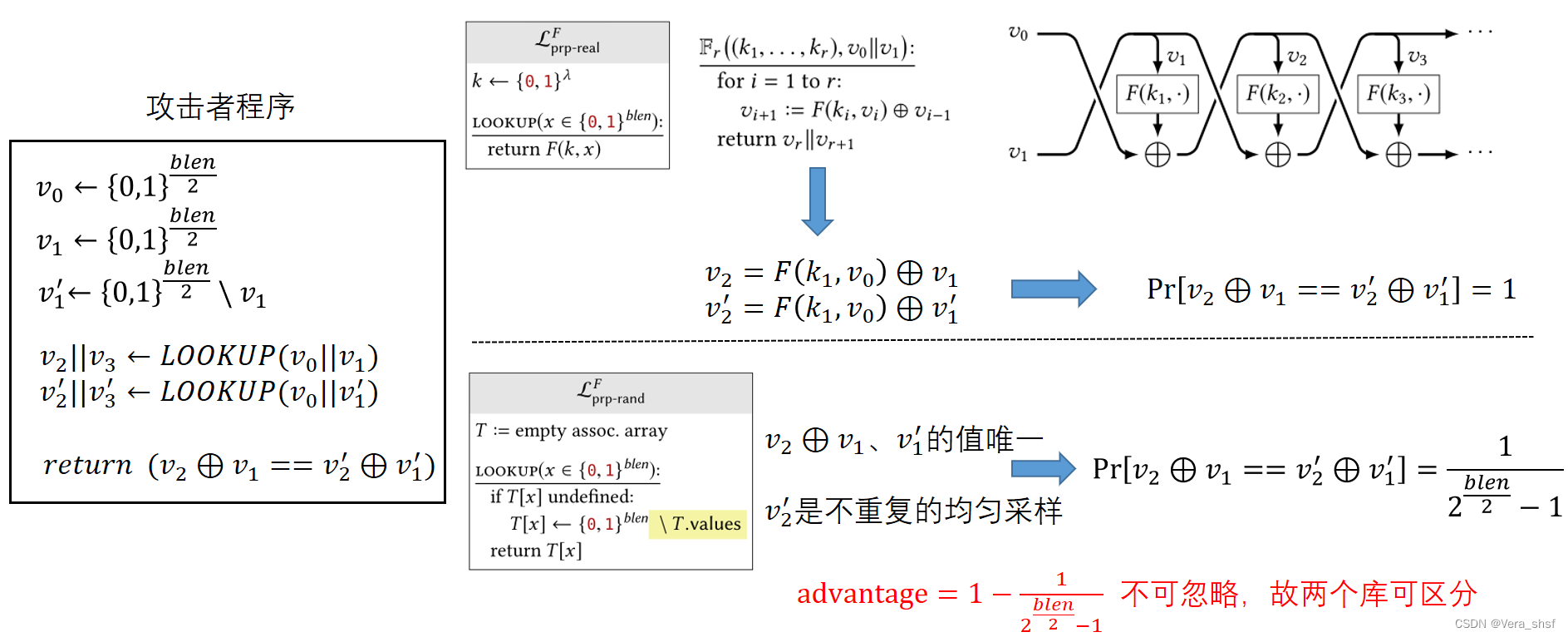
它其实就是由多个Feistel轮构成，目的就是将输入明文的部分再次进行加密。由于每一个轮是可逆的，因此整体也是可逆的（逆函数也在上图下方给出）。值得一提的是，每一个轮的密钥 k i k_i ki​可以不同，逆向解密时只要每一个轮对应使用之前加密时的密钥即可。关于Feistel密码的安全性，有以下结论：

定理6.4 如果 F : { 0 , 1 } λ × { 0 , 1 } λ → { 0 , 1 } λ F:\{0,1\}^\lambda\times\{0,1\}^\lambda\rightarrow\{0,1\}^\lambda F:{0,1}λ×{0,1}λ→{0,1}λ是一个安全的PRF，那么以 F F F为轮函数按照上图所示构造的Feistel密码 F 3 F_3 F3​是一个安全的PRP。

定理6.5 如果 F : { 0 , 1 } λ × { 0 , 1 } λ → { 0 , 1 } λ F:\{0,1\}^\lambda\times\{0,1\}^\lambda\rightarrow\{0,1\}^\lambda F:{0,1}λ×{0,1}λ→{0,1}λ是一个安全的PRF，那么以 F F F为轮函数按照上图所示构造的Feistel密码 F 4 F_4 F4​是一个安全的SPRP。

定理6.4说明3个轮的Feistel密码可以构建一个安全的PRF，但是该定理的证明超越本书内容。而2个轮的Feistel密码一定不是安全的PRP。然而 F 3 F_3 F3​并非一个安全的SPRP。不过定理6.5说明再增加一个轮（4个轮）就可以构建一个安全的SPRP，该定理的证明书中也未呈现。

2个轮的Feistel密码一定不是安全的PRP的证明 书上以练习题的形式给出，在此给出个人的解答。对于 F 2 F_2 F2​而言，它的输出是 v 2 ∣ ∣ v 3 v_2||v_3 v2​∣∣v3​，其中 v 2 = F ( k 1 , v 0 ) ⊕ v 1 v_2=F(k_1, v_0)\oplus v_1 v2​=F(k1​,v0​)⊕v1​。那么可以构建攻击者程序 A A A：调用两次库，两次输入分别为 v 0 ∣ ∣ v 1 v_0||v_1 v0​∣∣v1​、 v 0 ∣ ∣ v 1 ′ v_0||v_1' v0​∣∣v1′​（ v 1 ≠ v 1 ′ v_1\neq v_1' v1​=v1′​，也就是两次输入的前半段相同，后半段不同），调用结果分别为 v 2 ∣ ∣ v 3 、 v 2 ′ ∣ ∣ v 3 ′ v_2||v_3、v_2'||v_3' v2​∣∣v3​、v2′​∣∣v3′​，程序返回值为 v 2 ⊕ v 1 = ? v 2 ′ ⊕ v 1 ′ v_2\oplus v_1 \overset{?}{=}v_2'\oplus v_1' v2​⊕v1​=?v2′​⊕v1′​。显然如果这个库是 F 2 F_2 F2​，那么 A A A的返回值永远为真（因为输入只有后半段不一样，异或后消去）。但是如果这个库是PRP安全性定义中的随机库（rand），显然并非永远为真。由于程序执行过程中 v 2 ⊕ v 1 v_2\oplus v_1 v2​⊕v1​的结果是唯一的，而 v 1 ′ v_1' v1′​也是确定的，因此使得等式成立的 v 2 ′ v_2' v2′​也是唯一的。而 v 2 ′ v_2' v2′​是不重复均匀采样所得，因此恰好成立的概率是 1 2 b l e n 2 − 1 \frac{1}{2^{\frac{blen}{2}}-1} 22blen​−11​（这里 v 2 ′ v_2' v2′​必然不与 v 2 v_2 v2​相等，因为如果相等且等式成立，则 v 1 = v 1 ′ v_1=v_1' v1​=v1′​，矛盾。所以必然是剩余的 2 b l e n 2 − 1 2^\frac{blen}{2}-1 22blen​−1个元素中的一个）。因此 F 2 F_2 F2​与随机库的advantage为 1 − 1 2 b l e n 2 − 1 1-\frac{1}{2^{\frac{blen}{2}-1}} 1−22blen​−11​，不是可忽略的（ λ → ∞ \lambda \rightarrow \infin λ→∞时不趋向0），因此这两个库可区分，不满足PRP的安全性要求。

本章提到了PRG、PRF、PRP三个概念，其中PRG和PRF可以相互构造；安全的PRP在输入规模足够大时也是安全的PRF（转换引理），PRF可以用于构造PRP（对应本章的第二、四节的内容）。至于这三个概念（忽略安全性，只看定义），PRF和PRP可以说是最紧密的，PRF是函数，而PRP是输入输出空间相同的双射函数。而PRG和PRF相比，PRF有密钥空间而PRG没有。

而在实际应用当中，通常是使用PRP去构造所需要的PRF、PRG。目前并没有能够被证明的安全PRP（因为这个会解决P和NP问题）。但是目前有公认为安全的PRP：AES（Advanced Encryption Standard）。AES是一个加密标准，它是美国国家标准技术研究所（The National Institute of Standards & Technology，NIST）通过PRP设计比赛选拔所得。在2001年，比赛的胜者Rijndael密码成为了AES标准。目前并未发现攻破AES的方法。因此基于AES构造所得的PRF、PRG也是可以被认为是安全的。