| 求解反函数的导数,你真的会吗?(首先需要知道什么是反函数) | 您所在的位置:网站首页 › 反函数是倒数的意思吗 › 求解反函数的导数,你真的会吗?(首先需要知道什么是反函数) |
求解反函数的导数,你真的会吗?(首先需要知道什么是反函数)
|
一、前言 我们知道,函数的导数等于其对应的反函数导数的倒数,即: $$\frac{\mathrm{d} y}{\mathrm{d} x} = \frac{1}{\frac{\mathrm{d} x}{\mathrm{d} y}}$$ 但是,你真的会利用上面的性质计算反函数的导数吗? 难度评级: 相关文章:《反函数的性质汇总》 二、解析为了理解反函数的求导,我们首先要理解,所谓的反函数的“反”指的是什么?或者说,什么是反函数? 反函数的“反”指的是对应关系是相反的,而不是 $x$ 和 $y$ 是相反的—— 例如,在函数 $y = \textcolor{orange}{f} (x)$ 中,$y$ 和 $x$ 都是两个普通的变量符号,只有 $\textcolor{orange}{f}$ 才表示对应关系。也就是说,$y = \textcolor{orange}{f} (x)$ 和 $x = \textcolor{orange}{f} (y)$ 以及 $a = \textcolor{orange}{f} (b)$ 都表示的是同一个函数,因为他们的对应关系都是 $\textcolor{orange}{f}$. 接下来,我们需要搞明白,反函数的“反”是怎么“反”的? 我们知道,在函数 $\textcolor{orangered}{Y} = F(\textcolor{springgreen}{X})$ 中,自变量 $\textcolor{springgreen}{X}$ 可以通过对应关系 $F$ 对应到因变量 $\textcolor{orangered}{Y}$. 经过多轮对应,我们就可以找到两个集合——一个集合中的 $\textcolor{springgreen}{X}$ 可以通过对应关系 $F$ 和另一个集合中的 $\textcolor{orangered}{Y}$ 逐一对应。 那么,如果我们可以找到另一个对应关系 $F^{-1}$, 使得上面集合中的 $\textcolor{orangered}{Y}$ 可以通过对应关系 $F^{-1}$ 逐一对应到上面的集合 $\textcolor{springgreen}{X}$, 那么,$F^{-1}$ 与 $F$ 就是反函数。 如果绘制成示意图就是如图 01 这样的(其中虚线表示对应关系,蓝色和红色箭头与虚线的趋势是一致的,但根据箭头可知,对应方向是相反的): 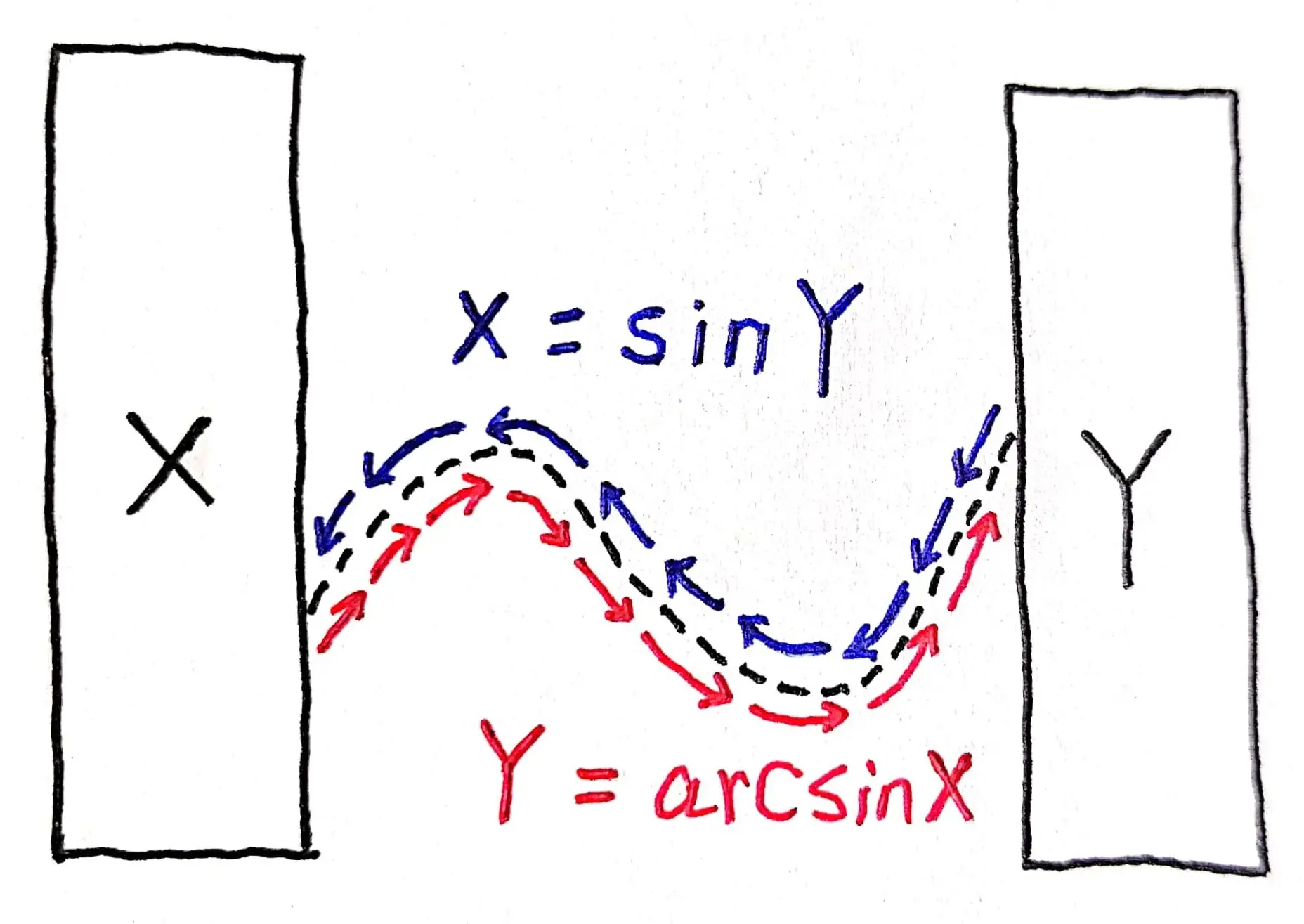 图 01. 图 01.
从上面的分析可以看出来,其实函数 $F$ 与其反函数 $F^{-1}$ 表示的都是同样两个集合之间的同样的对应关系,只不过这个对应过程是反过来的。 明白了上面的过程我们就可以知道,$y=\arcsin x$ 和 $x = \sin y$ 互为反函数,因为 $\arcsin$ 和 $\sin$ 是刚好相反的对应过程: $$y=\arcsin x \Rightarrow \textcolor{orange}{\sin} y = \textcolor{orange}{\sin}(\arcsin x) \Rightarrow \sin y = x$$ 同样的,$y = x^{3}$ 的反函数是 $x = y^{\frac{1}{3}}$, 因为: $$y = x^{3} \Rightarrow y^{\textcolor{orange}{ \frac{1}{3} }} = (x^{3})^{\textcolor{orange}{ \frac{1}{3} }} \Rightarrow y^{\frac{1}{3}} = x$$ 但是,为了符合一般的书写习惯,我们有时候也将 $x = \sin y$ 写成 $y = \sin x$, 这也就导致原本 $y=\arcsin x$ 和 $x = \sin y$ 的函数图像是完全重合的,但 $y=\arcsin x$ 和 $y = \sin x$ 的函数图像则是关于 $y=x$ 对称的。那么,函数图像不相同的 $x = \sin y$ 和 $y = \sin x$ 还是同一个函数吗? 如图 02 和 03 所示,红色实线表示 $\textcolor{red}{ x = \sin y }$, 蓝色实线表示 $\textcolor{blue}{y = \sin x}$, 绿色虚线表示 $y=x$: 其实,讨论两个函数是否一样,关键看自变量是谁:当我们将 $y = \arcsin x$ 的反函数写成 $x = \sin \textcolor{orange}{y}$ 时,$\textcolor{orange}{y}$ 是自变量,而当我们将 $y = \arcsin x$ 的反函数写成 $y = \sin \textcolor{yellow}{x}$ 时,$\textcolor{yellow}{x}$ 是自变量—— $y = \sin \textcolor{yellow}{x}$ 中的自变量 $\textcolor{yellow}{x}$ 其实是 $\textcolor{pink}{y} = \arcsin x$ 中的 $\textcolor{pink}{y}$——这里的 $\textcolor{yellow}{x}$ 和 $\textcolor{pink}{y}$ 表示都是同一个集合,只是用的符号不同而已。 但是,如果函数与反函数表示的都是两个集合之间同样的但方向相反的对应关系,那么,二者的函数图像应该是相同的。或者说,函数 $y=\arcsin x$ 与其反函数 $x = \sin y$ 的函数图像是完全重合的,但为什么函数 $y=\arcsin x$ 与反函数的另一种写法 $y = \sin x$ 的函数图像却是关于 $y = x$ 对称的呢? 产生上面这个问题的主要原因是“视觉错误”,其实,以 $y$ 为自变量的反函数 $x = \sin y$ 和以 $x$ 为自变量的反函数 $y = \sin x$ 的函数图像也是“重合”的,只不过,当我们把 $x = \sin y$ 的函数图像绘制在一般的平面直角坐标系中时,看上去是以 $x$ 为自变量而不是以 $y$ 为自变量,只要我们做一些镜像和旋转变换就可以发现,这其实是同一个函数图像。 例如,我们有 $y = \sin x$ 的函数图像如下: 现在,我们把 $y = \sin x$ 的函数图像做一个水平翻转(相当于把纸从右向左翻过来,从反面看): 之后,我们再把上面经过水平翻转的图像顺时针逐渐旋转 $90$ 度: 然后我们就会发现,我们得到了关于 $y=x$ 对称的两个函数图像,但由于是翻转和旋转得到的,因此,这两条函数曲线一定是属于同一个函数的: Tips: 我们曾经可能学过这样的求反函数的方法:先交换 $x$ 和 $y$, 即 $y = \arcsin x$ $\Rightarrow$ $x = \arcsin y$, 然后再想办法写成 $x$ 为自变量,$y$ 为因变量的形式,即 $x = \arcsin y$ $\Rightarrow$ $\sin x = \sin (\arcsin y)$ $\Rightarrow$ $y = \sin x$. 但是,这样做有两个问题,一是没有说明反函数真正“反”的是对应关系而不是变量的符号,二是没有指明谁才是自变量。 2. 反函数如何求导由于,在求导的时候,我们需要保证,函数与其反函数的式子中所使用的变量的符号相同时表示的集合也相同,也就是说,$x$ 一定表示 $x$ 所在的集合,$y$ 一定表示 $y$ 所在的集合—— 因此,如果要用原函数 $y = \arcsin x$ 的反函数的导数的倒数表示原函数的导数,那么,这个反函数只能写成 $x = \sin y$, 因为,在 $y = \arcsin x$ 和 $x = \sin y$ 这两个式子中,变量 $x$ 和 $y$ 表示的集合都是对应相同的。 于是: $$(\arcsin x)^{\prime} = \frac{1}{\sqrt{1 – x^{2}}} \tag{1}$$ 又: $$\frac{1}{(\sin y)^{\prime}} = \frac{1}{\cos y} = \frac{1}{\sqrt{1 – \sin^{2} y}} \Rightarrow x = \sin y \Rightarrow \frac{1}{\sqrt{1 – x^{2}}} \tag{2}$$ 于是,(1) 式和 (2) 式刚好相等,即原函数的导数 $(\arcsin x)^{\prime}$ 刚好等于其反函数导数的倒数 $\frac{1}{(\sin y)^{\prime}}$ 又例如,$y = x^{3}$ 和 $x = y^{\frac{1}{3}}$ 是反函数,则: $$(x^{3})^{\prime} = 3x^{2}$$ $$\frac{1}{(y^{\frac{1}{3}})^{\prime}} = \frac{1}{\frac{1}{3} y^{\frac{-2}{3}}} = \frac{1}{\frac{1}{3} (y^{\frac{1}{3}})^{-2}} \Rightarrow x = y^{\frac{1}{3}} \Rightarrow \frac{1}{\frac{x^{-2}}{3}} = 3x^{2}$$ 涵盖高等数学基础概念、解题技巧等内容,图文并茂,计算过程清晰严谨。 线性代数以独特的视角解析线性代数,让繁复的知识变得直观明了。 特别专题通过专题的形式对数学知识结构做必要的补充,使所学知识更加连贯坚实。 让考场上没有难做的数学题! 相关文章: 反函数的性质汇总 对于无法凑项消去的反常积分可以尝试倒数代换或者三角代换 反三角函数 $\arcsin$ 的常用特殊值(A004) 计算平面曲线的弧长需要知道积分上下限,但如果这个积分上线限题目中没有给出该怎么办? 存在两类及以上不同函数的式子就尝试用分部积分:$\int$ $\frac{\arcsin \sqrt{x} + \ln x}{\sqrt{x}}$ $\mathrm{d} x$ 计算微分方程 $y^{\prime \prime}$ $+$ $2 m y^{\prime}$ $+$ $n^{2} y$ $=$ $0$ 满足一定条件特解的无穷限反常积分 用两种不同的思路解决一道隐函数变量替换的题目 arcsin(sin x) 一定等于 x 吗?不一定哦! 解题的时候一定要穷尽所有可能的答案 对 $\int$ $\frac{f(\arcsin x)}{\sqrt{1-x^{2}}}$ $\mathrm{d} x$ 凑微分的计算方法(B006) 适时而止,更简单:$\int$ $e^{x}$ $\arcsin \sqrt{1-e^{2x}}$ $\mathrm{d} x$ 当二重积分的积分区域不是圆形但被积函数和圆形有关时,也可以尝试使用极坐标系求解 这道题中的矩阵虽然很“宽”,但其实是一个单列矩阵 $\sin [2 \arcsin y]$ 等于多少? 集火攻击:多种方法解一道题 计算微分方程 $y$ $y^{\prime \prime}$ $+$ $2$ $(y^{\prime})^{2}$ $=$ $0$ 满足给定初始条件的特解 通过二元复合函数判断一元函数的极值点条件 证明 $(\arcsin x)^{\prime}$ $=$ $\frac{1}{\sqrt{1-x^{2}}}$ 二重积分中经常使用转变积分区域的形式去根号 求导一定要“彻底”:以 $\arcsin \sqrt{x}$ 为例 三元隐函数的复合函数求导法则(B012) 这道题没说函数可导,所以就不能求导了嘛? $\cos (\arcsin y)$ 等于多少? 计算微分方程 $y^{\prime \prime}$ $+$ $y^{\prime}$ $-$ $2 y$ $=$ $(6x + 2) e^{x}$ 满足指定条件的特解 这道不定积分题有三个不同的答案:但每个答案都是对的 |
【本文地址】