| 凸优化,对偶问题,Slater条件,KKT条件总结 | 您所在的位置:网站首页 › 原问题和对偶问题的关系图 › 凸优化,对偶问题,Slater条件,KKT条件总结 |
凸优化,对偶问题,Slater条件,KKT条件总结
|
文章目录
一、标准优化问题\原始优化问题二、对偶问题三、原始问题和对偶问题的关系(弱对偶与强对偶)四、凸集1. 凸集定义2. 常见的凸集
五、凸函数六、凸优化问题七、理解凸问题与强对偶关系八、KKT条件总结
一、标准优化问题\原始优化问题
若 f ( x ) , c i ( x ) , h j ( x ) f(x), c_i(x), h_j(x) f(x),ci(x),hj(x)是定义在 R n R^n Rn上的连续可微函数。考虑如下有约束的最优化问题: 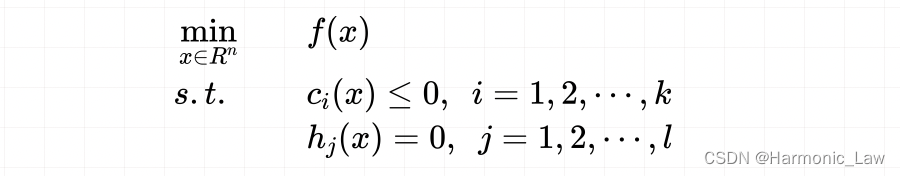
表示在所有满足 c i ( x ) ≤ 0 c_i(x)\leq0 ci(x)≤0 及 h j ( x ) = 0 h_j(x)=0 hj(x)=0 的 x x x 中找出使 f 0 ( x ) f_0(x) f0(x) 最小的 x x x;这就是有约束优化问题的标准形式,或称为原始形式 对目标函数和所有约束函数的定义域的集合,也就是该优化问题的 可行解集合 ( D D D )或 定义域 D = ⋂ i = 1 k d o m c i ⋂ ⋂ j = 1 l d o m h i ⋂ d o m f \begin{aligned} D=\bigcap_{i=1}^k \mathrm{dom}\:c_i\:\bigcap\:\bigcap_{j=1}^l \mathrm{dom}\:h_i\bigcap \mathrm{dom}\:f \end{aligned} D=i=1⋂kdomci⋂j=1⋂ldomhi⋂domf 这样一个优化问题,拥有 k + l k+l k+l个约束条件,计算起来是比较复杂的。我们使用 广义拉个郎日函数 就可以将约束条件结合到一个等式中去: 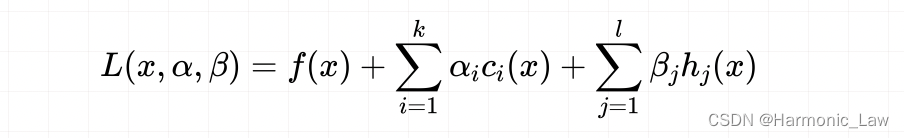
其中 α i > 0 \alpha_i>0 αi>0 那么原始优化问题就会与下方问题等价: 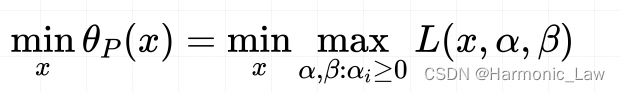
因为「在有约束的情况下」,如果求 max L ( x , α , β ) \max L(x,\alpha,\beta) maxL(x,α,β),回归到原始问题的约束条件中,意味着将 c i ( x ) c_i(x) ci(x) 和 h j ( x ) h_j(x) hj(x) 都取最大值,这里对应的都是 0 0 0,只剩下了,因此 max L ( x , α , β ) = f ( x ) \max L(x,\alpha,\beta)=f(x) maxL(x,α,β)=f(x) 而「在无约束的情况下」,意味着没有了 c i ( x ) c_i(x) ci(x) 和 h j ( x ) h_j(x) hj(x) 的约束,那么可以将 max L ( x , α , β ) \max L(x,\alpha,\beta) maxL(x,α,β) 取无穷大,这样就得到了 max L ( x , α , β ) = + ∞ \max L(x,\alpha,\beta)=+\infty maxL(x,α,β)=+∞ 那么: min θ P ( x ) = min { f ( x ) , + ∞ } = min f ( x ) \begin{aligned} \min\theta_P(x)=\min \{f(x),+\infty\}=\min f(x) \end{aligned} minθP(x)=min{f(x),+∞}=minf(x) 接着对这个原始问题的最优值就可以写成: 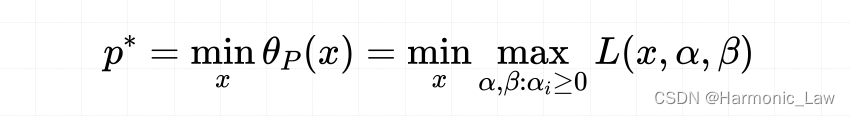
这样就转为了极小极大值的问题,记为 p ∗ p^* p∗ 二、对偶问题还是回到广义拉格朗日函数问题上。 如果这次我们是对 x x x 求最小值,那么未知的就是 α \alpha α 和 β \beta β 参数 对偶函数记为: 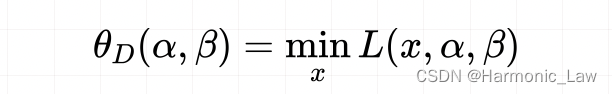
对偶问题记为: max α , β , α ≥ 0 θ D ( α , β ) = max α , β , α ≥ 0 min x L ( x , α , β ) \begin{aligned} \max_{\alpha,\beta,\alpha\geq0}\theta_D(\alpha,\beta)=\max_{\alpha,\beta,\alpha\geq0}\min_x L(x,\alpha,\beta) \end{aligned} α,β,α≥0maxθD(α,β)=α,β,α≥0maxxminL(x,α,β)注意:此时对偶问题也有约束条件: ∇ L x ( x , α , β ) = 0 α ≥ 0 \begin{aligned} \nabla L_x(x,\alpha,\beta)=0\\ \alpha\geq0 \end{aligned} ∇Lx(x,α,β)=0α≥0对偶问题的最优值就可以写成: 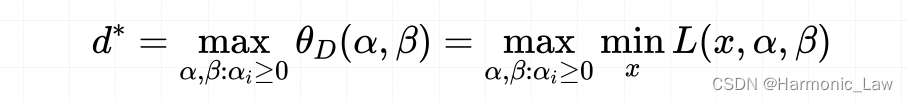 三、原始问题和对偶问题的关系(弱对偶与强对偶)
三、原始问题和对偶问题的关系(弱对偶与强对偶)
可以看出: 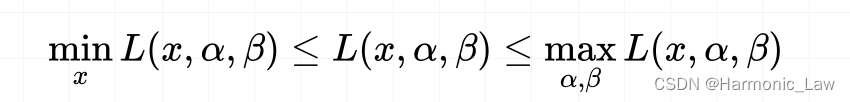
最终得到的结果表明对偶问题的最优解总是小于等于原始问题的最优解: 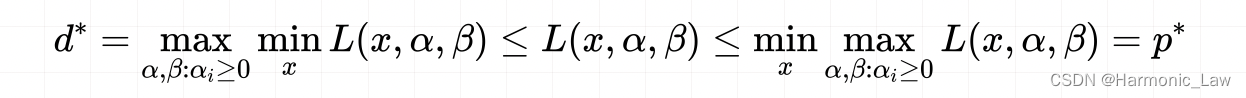 d
∗
≤
p
∗
d^*\leq p^*
d∗≤p∗,这种性质称为弱对偶(weak duality)若恰好
d
∗
=
p
∗
d^*= p^*
d∗=p∗ ,这种情况称为强对偶(strong duality);
p
∗
−
d
∗
p^*-d^*
p∗−d∗ 称为对偶间隙(duality gap)
d
∗
≤
p
∗
d^*\leq p^*
d∗≤p∗,这种性质称为弱对偶(weak duality)若恰好
d
∗
=
p
∗
d^*= p^*
d∗=p∗ ,这种情况称为强对偶(strong duality);
p
∗
−
d
∗
p^*-d^*
p∗−d∗ 称为对偶间隙(duality gap)
那么什么时候才可以满足强对偶关系呢? 若函数 f ( x ) f(x) f(x) 和 c i ( x ) c_i(x) ci(x) 是凸函数, h i ( x ) h_i(x) hi(x) 是仿射函数;并且假设不等式约束 c i ( x ) c_i(x) ci(x) 是严格可行的,即存在 x x x 对所有的 i 有 c i ( x ) < 0 c_i(x)x1,x2.....xk} ,则其凸包可以表示为: C = { ∑ i = 1 k θ i x i ∣ ∑ θ i = 1 , θ i ≥ 0 } \begin{aligned} C=\{\sum_{i=1}^k\theta_i x_i|\sum\theta_i = 1,\theta_i \ge 0\} \end{aligned} C={i=1∑kθixi∣∑θi=1,θi≥0} 3. 半空间(Halfspaces):类似的,有半空间定义为: C = { x ∣ W T x ≤ 0 } ( W ≠ 0 ) \begin{aligned} C=\{x|W^Tx\leq0\}(W\neq0) \end{aligned} C={x∣WTx≤0}(W=0) 4. 凸集有以下特点: 如果A和B是凸集,则它们的交集A∩B也是凸集。如果A和B是凸集,则它们的并集A∪B也是凸集。如果A和B是凸集,则它们的直和A+B也是凸集。 五、凸函数设集合 C C C 是非空凸集, f f f 是定义在 C C C 上的函数,如果对于任意的 x , y ∈ C , α ∈ ( 0 , 1 ) x,y\in C,\alpha\in(0,1) x,y∈C,α∈(0,1) 均有: 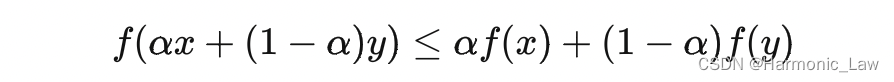
则称 f f f 为 C C C 上的凸函数 也就是如果函数 f f f是凸函数,需要满足: 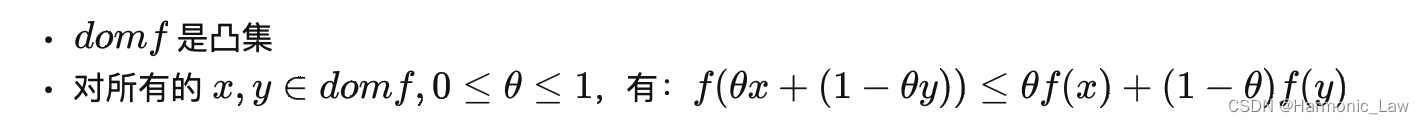
图解如下: 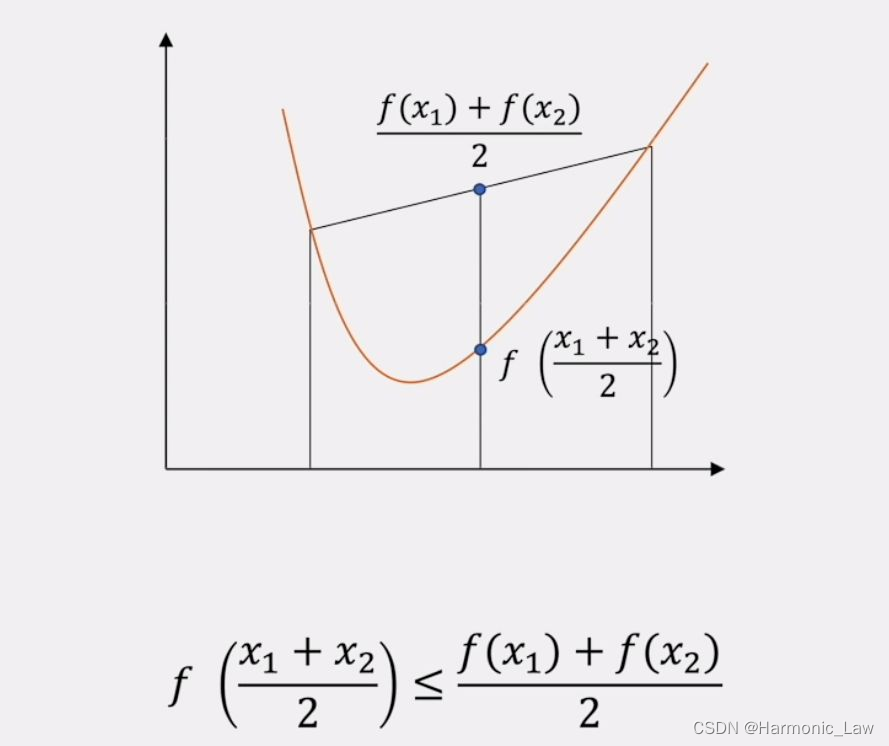 六、凸优化问题
六、凸优化问题
对于一般的有约束优化问题,我们求得的解可能只是 局部最优值,而不是 全局最优解。我们将任何局部最优解就是全局最优解的优化问题称为 凸优化问题,而不满足凸优化问题的优化问题称为非凸优化问题 对于非凸优化问题,在求解时存在以下困难: 多个局部最优解:非凸优化问题可能存在多个不同的局部最优解,使得算法在搜索过程中很难找到全局最优解。寻找初始点:由于非凸函数具有多个局部最优解,寻找一个好的初始点对于算法的收敛性和稳定性是很重要的,但是如何选择一个好的初始点是一个挑战。算法收敛性:由于非凸函数的复杂性,算法的收敛性无法保证,即使算法在某些情况下收敛,也无法保证收敛到全局最优解。而凸优化问题有以下优势 确定性解:凸优化问题在满足一定条件下,可以保证存在唯一的全局最优解,因此可以得到确定性的解。收敛性保证:针对凸优化问题,已经研究出了很多高效的算法,这些算法具有收敛性的保证,可以在有限的迭代次数内找到全局最优解。简单且高效的求解方法:凸优化问题可以使用诸如梯度下降、共轭梯度等简单且高效的求解方法来找到最优解。综上所述,凸优化问题相比非凸优化问题具有更好的求解性质和算法效率。 因此我们希望从一般性的优化问题中找出哪些“凸优化问题”,最终得到凸优化问题的定义: 凸问题的标准形式如下: 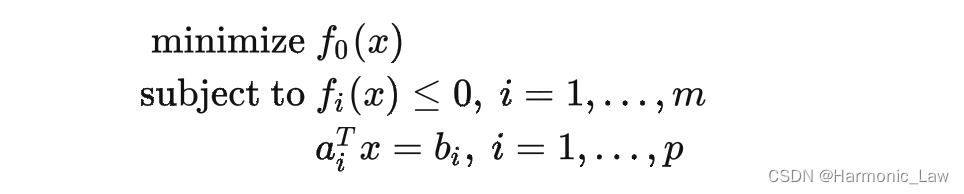
其中需要注意: f 0 ( x ) f_0(x) f0(x)是凸函数 f i ( x ) f_i(x) fi(x)是凸函数 h i ( x ) = a i T x − b h_i(x)=a_i^Tx-b hi(x)=aiTx−b是仿射函数对于凸问题,局部最优即是全局最优!(证明过程可查看参考文献5) 七、理解凸问题与强对偶关系回到上文,我们研究凸问题是因为一般的凸问题就满足了强对偶条件(更加严格来说需要满足Slater条件),这样就可以通过求解原始问题的对偶问题来简化求解原问题 对于凸问题,由于局部最优解就是全局最优解,确实可以直接使用算法来求解原问题。但是研究其对偶问题可以带来一些额外的优势。首先,对偶问题可以提供原问题的下界,在求解原问题时可以作为参考。其次,对偶问题可以帮助我们理解原问题的结构和特性,进而设计更加有效的求解算法。此外,对偶问题在某些情况下也可以比原问题具有更简洁的形式,从而更容易求解。因此,通过研究对偶问题来求解凸问题是一种常用的方法。 将凸优化问题与标准优化问题进行对比:发现凸优化问题就是将标准优化问题进行了三个限制,于是标准优化问题就变成了凸问题,并且一般情况下满足强对偶关系,我们接下来来理解这 三个限制 f 0 ( x ) f_0(x) f0(x)是凸函数 f i ( x ) f_i(x) fi(x)是凸函数 h i ( x ) = a i T x − b h_i(x)=a_i^Tx-b hi(x)=aiTx−b是仿射函数原问题: min x max α , β , α ≥ 0 L ( x , α , β ) \begin{aligned} \min_x\max_{\alpha,\beta,\alpha\geq0} L(x,\alpha,\beta) \end{aligned} xminα,β,α≥0maxL(x,α,β) 对偶问题 max α , β , α ≥ 0 min x L ( x , α , β ) \begin{aligned} \max_{\alpha,\beta,\alpha\geq0}\min_x L(x,\alpha,\beta) \end{aligned} α,β,α≥0maxxminL(x,α,β) 简化拉格朗日函数方便进行理解: 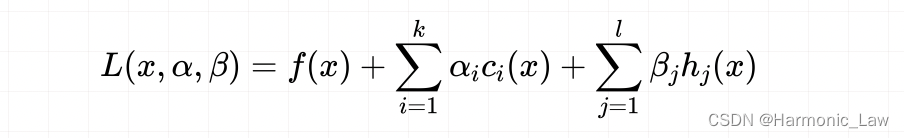
令 t = f ( x ) , α T u = ∑ i = 1 k α i c i ( x ) , β T v = ∑ j = 1 l α i h i ( x ) = 0 t=f(x),\:\,\alpha^Tu=\sum_{i=1}^k\alpha_ic_i(x),\:\,\beta^Tv=\sum_{j=1}^l\alpha_ih_i(x)=0 t=f(x),αTu=∑i=1kαici(x),βTv=∑j=1lαihi(x)=0 那么拉格朗日函数可以表示为: L ( x , α , β ) = t + α T u + β T v \begin{aligned} L(x,\alpha,\beta)=t+\alpha^Tu+\beta^Tv \end{aligned} L(x,α,β)=t+αTu+βTv 此时原问题和对偶问题的可行域不太相同了: 原问题可行域: G 1 = { ( t , u , v ) ∣ t = f ( x ) , u = c i ( x ) , v = h i ( x ) , x ∈ D } G_1=\{(t,u,v) | t=f(x),u=c_i(x),v=h_i(x),x\in D\} G1={(t,u,v)∣t=f(x),u=ci(x),v=hi(x),x∈D} 对偶问题可行域: G 2 = { ( t , u , v ) ∣ t = f ( x ) , u = c i ( x ) , v = h i ( x ) , x ∈ R n } G_2=\{(t,u,v) | t=f(x),u=c_i(x),v=h_i(x),x\in R^n\} G2={(t,u,v)∣t=f(x),u=ci(x),v=hi(x),x∈Rn} 可以看出来对偶问题的可行域是属于全空间的 将拉格朗日进行简化后,原问题和对偶问题形式上也进行了改变: 原问题: min x { t ∣ ( t , u , v ) ∈ G 1 , u ≤ 0 } \min_x\{t|(t,u,v)\in G_1,u\leq0\} minx{t∣(t,u,v)∈G1,u≤0} 对偶问题: max α , β min x { t + α T u + β T v ∣ ( t , u , v ) ∈ G 2 , α ≥ 0 } \max_{\alpha,\beta}\min_x\{t+\alpha^Tu+\beta^Tv|(t,u,v)\in G_2,\alpha\ge0\} maxα,βminx{t+αTu+βTv∣(t,u,v)∈G2,α≥0} 那么接下来我们来画出原问题与对偶问题的可行域,但是我们的可行域是一个三维空间,画出来不易理解;注意到可行域点的坐标 ( t , u , v ) (t,u,v) (t,u,v)中,第三个维度的坐标值 v v v 实际上始终为 0 0 0,所以我们可以只画出二维的图像。 但是需要注意:即使画出的是二维的图像, v = h i ( x ) = 0 v=h_i(x)=0 v=hi(x)=0 仍然会影响 x x x 取值,也就会影响 t = f ( x ) 和 u = c i ( x ) t=f(x)和u=c_i(x) t=f(x)和u=ci(x) 的取值 我们假设坐标 ( t , u , v ) (t,u,v) (t,u,v)的取值集合在二维坐标系下如下图所示: 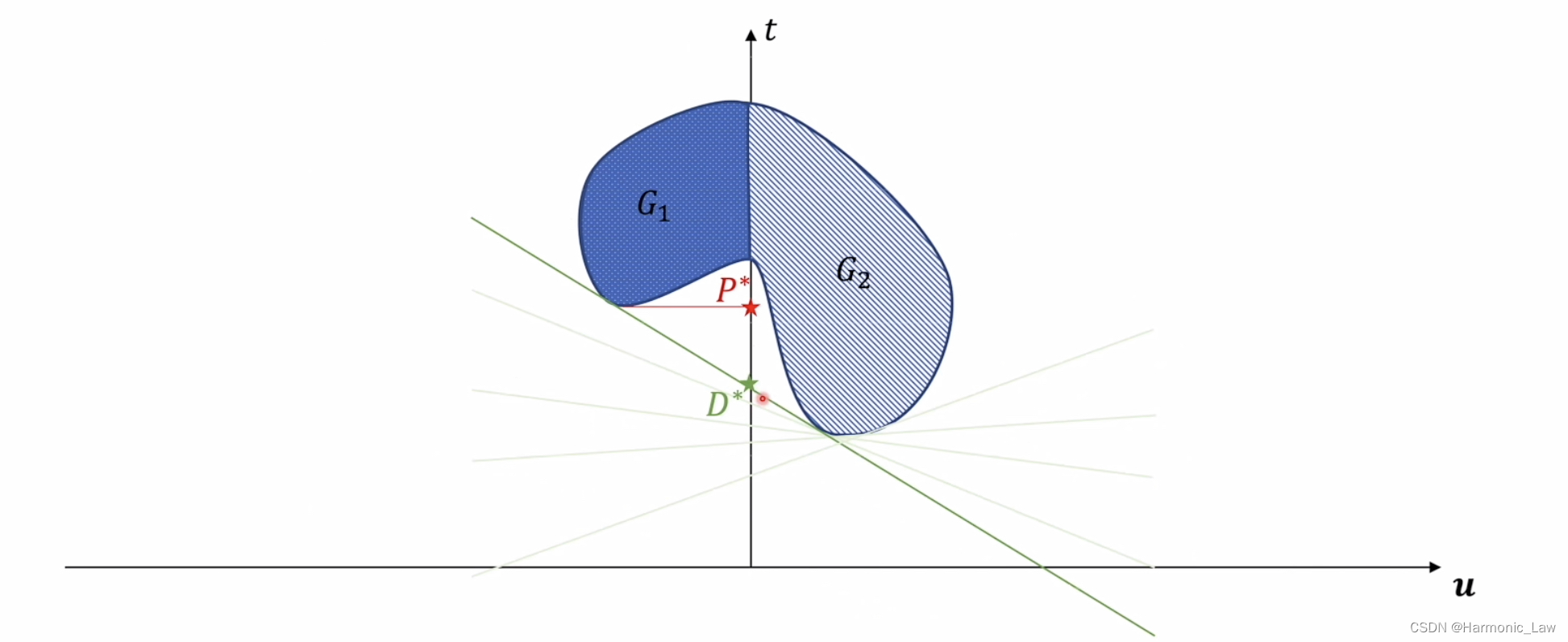
可以看出对偶问题最优解 D ∗ D^* D∗总是小于原始问题最优解 P ∗ P^* P∗;那么什么时候会相等呢? 只有当坐标 ( t , u , v ) (t,u,v) (t,u,v) 取值的集合为凸集的时候,才会出现强对偶关系;如下图所示: 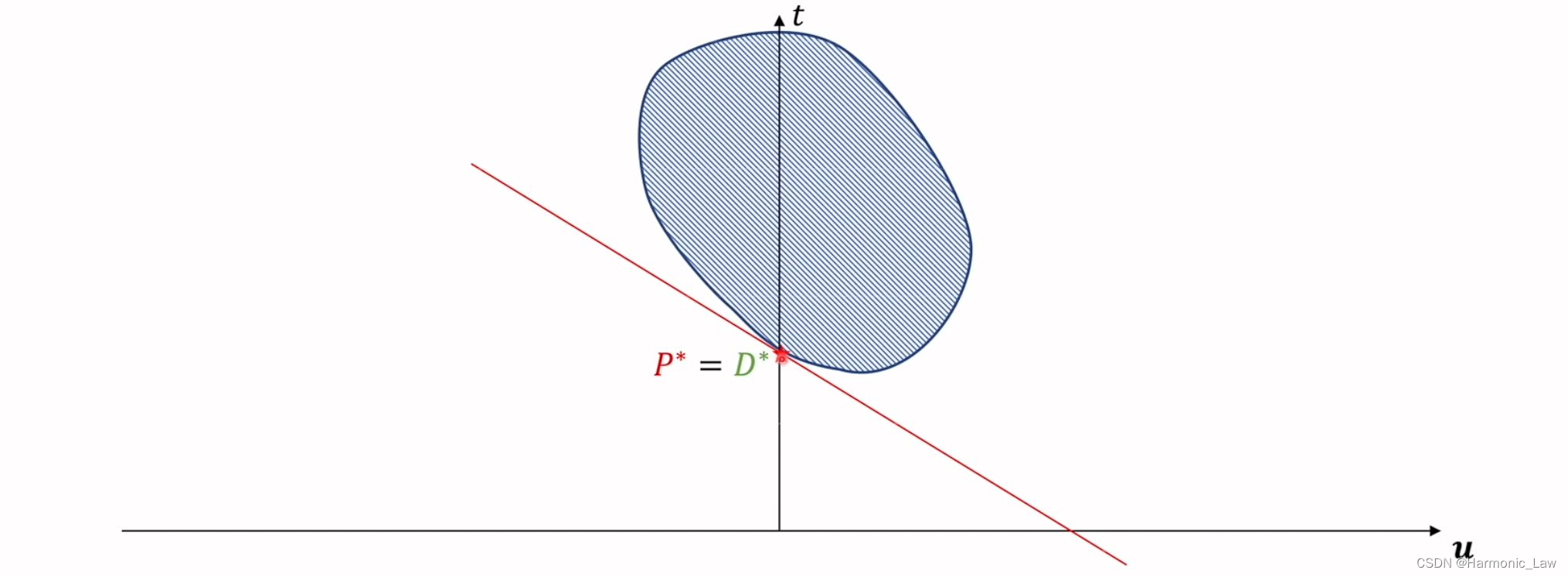
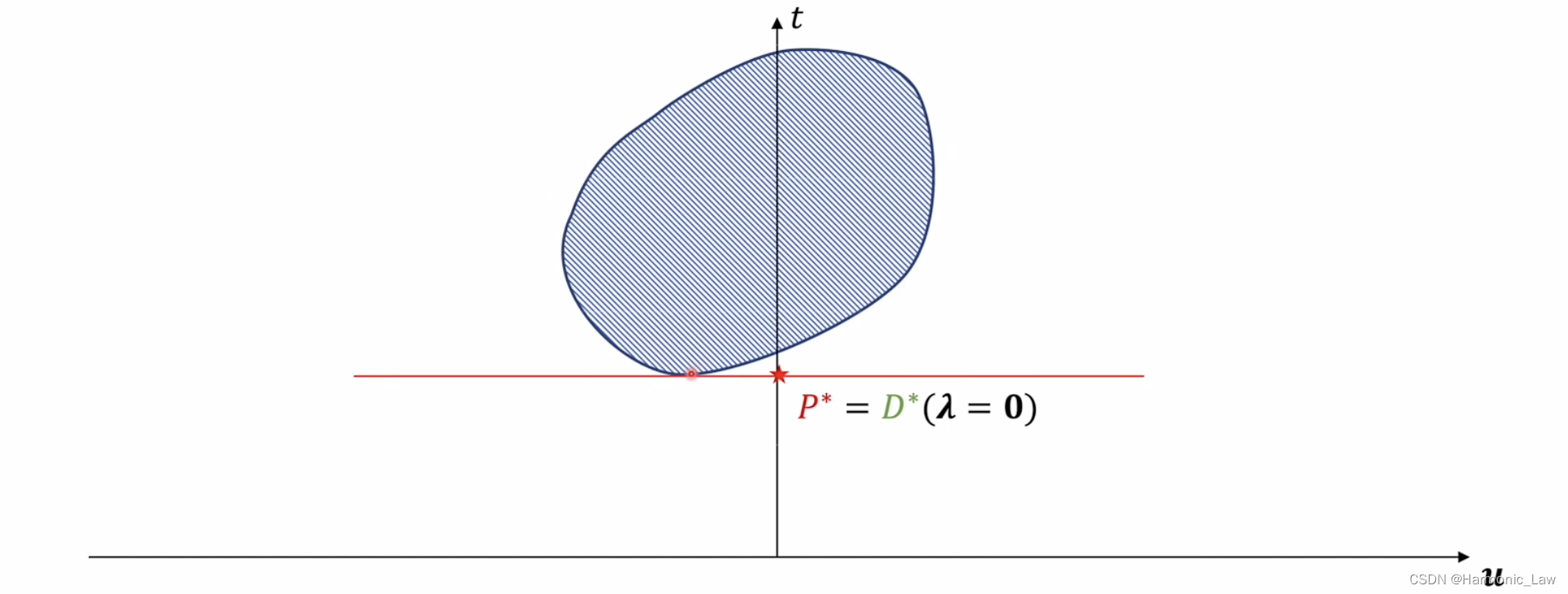
那么要想要坐标 ( t , u , v ) (t,u,v) (t,u,v) 取值的集合为凸集, t = f ( x ) , u = c i ( x ) , v = h i ( x ) = 0 t=f(x),u=c_i(x),v=h_i(x)=0 t=f(x),u=ci(x),v=hi(x)=0 需要满足什么条件呢? 需要满足的条件就是上述对一般优化问题进行的三个限制 八、KKT条件KKT(Karush-Kuhn-Tucker)条件 是一般优化问题最优解的必要条件;通常可根据KKT条件解出一些值,然后判断其中哪些是最优解,从而解决优化问题。 对于一般优化问题: 
KKT条件包括 
需要注意: 对于一般的优化问题(不一定是凸问题),各个函数可微且满足强对偶关系,则KKT条件是最优解的 必要条件若原问题为凸问题,各个函数可微且对偶间隙为0,则KKT条件是最优解的 充要条件通俗来讲就是一般优化问题的最优值所对应的点是一定满足KKT条件的,但是满足KKT条件的点不一定是最优值对应的点;但凸问题的最优值点一定满足KKT条件,满足KKT条件的点一定是最优值点 注意:一般的凸问题满足强对偶关系,而严格来说凸问题需要满足Slater条件才是强对偶关系,也就是说Slater条件是凸问题满足强对偶关系的 充分条件 我们一般研究凸问题,那么KKT条件也可以作为充要条件来使用;而原问题是否满足强对偶关系我们通常通过 Slater条件 来证明,所以在应用的角度上,我们将范围缩小,经常使用如下的KKT条件来进行应用计算。 若函数 f ( x ) f(x) f(x) 和 c i ( x ) c_i(x) ci(x) 是凸函数,h_i(x) 是仿射函数(凸问题);并且假设不等式约束 c i ( x ) c_i(x) ci(x) 是严格可行的,即存在 x x x,对所有的 i i i 有 c i ( x ) < 0 c_i(x) |
【本文地址】