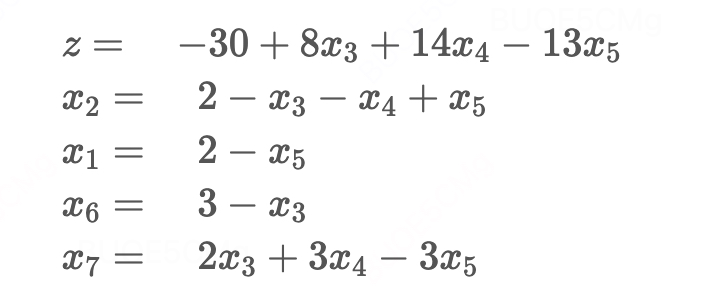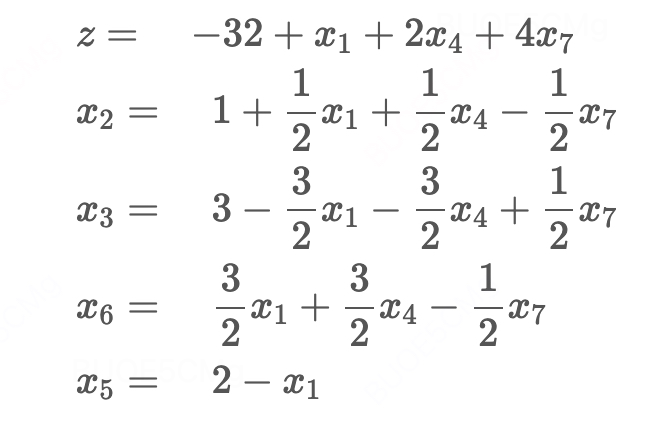| 运筹学基础(一)求解线性规划的单纯形法详解 | 您所在的位置:网站首页 › 单纯形法的算法思想 › 运筹学基础(一)求解线性规划的单纯形法详解 |
运筹学基础(一)求解线性规划的单纯形法详解
|
文章目录
前言线性规划的标准形式一个例子理解单纯形法1. 将线性规划转化为标准形式2. 找到一个初始可行解3. 旋转操作4. 重复旋转
一些badcase退化初始解不是可行解以及无解的情况找不到有限制条件的替入变量——无界解
时间复杂度附录参考资料
前言
大学的《运筹学》课程中,手算单纯形法是期末的必考题了!(记得期末考试前一周,几个经常逃课的同学来我宿舍楼下,叫了辆车载我去星巴克给他们讲解这个算法,活活讲了一个多小时他们才听懂,不知道最后及格了没哈哈!)当时已经觉得是信手拈来了,但是时间久了+计算过程本身也比较繁琐,慢慢就忘了。后面为了应付面试,又拾起过,但是面完试细节又给忘了,只记得是在可行域的顶点上来回搜索。 这次想完整的梳理一篇文章(本文是跟着某位大佬的博客,在某些地方掺杂了一些自己的思考和补充知识点汇总的),帮助自己再次回顾和更深的理解单纯形法,原因是在看一些更高阶的算法时,常常需要单纯形法的预备知识!不然就很难继续往下看懂了。 废话有点多了,进入正题吧! 线性规划的标准形式因为单纯形法就是建立在标准形式之上,在解空间沿着边界的顶点(称为单纯形,“单纯形” 用于描述凸多面体中的极端点或顶点),逐步改进目标值。所以先快速过一下如何将一个线性规划问题转为标准形式! 标准形式三要素: 目标函数 m i n i m i z e minimize minimize 或者 m a x i m i z e maximize maximize都行,不同教材选择不一样,本文用 m i n i m i z e minimize minimize; 不是minimize怎么办,取负就可以了。 约束条件等式化; 不是等式怎么办?如果是 > = >= >=,左端减去松弛变量即可,如果是 < = 非基变量。 3. 旋转操作【第一轮旋转】 step 1: 在目标函数里找到一个系数为负的非基变量,作为入基变量 这么做的原因是,我们现在的目标函数是 m i n i m i z e minimize minimize,现在有一个初始可行解了,我们怎么找到一个目标值更小的解呢?只要将目标函数里系数为负的变量,在满足约束的前提下,进一步减小就可以了!(这与在单纯形表中计算检验数 reduce cost 是一个思想,对于检验数的深入理解,见我的文章运筹学基础(四):单纯形法中检验数(reduced cost)的理解) 这里假设我们选取了 x 1 x_1 x1(这里有一个技巧,总是选择符合条件的下标最小的非基变量,原因是为了避免退化,后面badcase里会再讲)。
step2:将入基变量用基变量表示,准备替换: update一下,今天看一本优化相关的书,他提到的如果选择出基变量的方法是:用约束方程中的常数项除以入基变量的系数,选择比值最小的那个(其实本质上也是选择约束最紧的那个),我觉得这个方式更简洁明了! 因为我们选择的 x 1 x_1 x1作为入基变量,上面第2个式子和第3个式子中都有 x 1 x_1 x1,用上述方法除完分别是:4/1=1, 2/1=2,因此选择 x 1 = 2 − x 5 x_1= 2-x_5 x1=2−x5。 因为我们选择的 x 1 x_1 x1作为入基变量,上面第2个式子和第3个式子中都有 x 1 x_1 x1,我们选择哪个来表示 x 1 x_1 x1呢? 我们来比较一下: 用第2个式子表示 x 1 = 4 − x 2 − x 3 − x 4 x_1 =4-x_2-x_3-x_4 x1=4−x2−x3−x4,即 x 1 ≤ 4 x_1 \leq 4 x1≤4,用第3个式子表示 x 1 = 2 − x 5 x_1= 2-x_5 x1=2−x5,即 x 1 ≤ 2 x_1 \leq 2 x1≤2我们要选择更严格/紧的那个(也是为了防止退化,后面的badcase会讲),因此,最后将 x 1 x_1 x1表示成: x 1 = 2 − x 5 x_1 = 2 - x_5 x1=2−x5 step 3: 将入基变量的表达式,带入目标函数,完成转动 一次转动选择一个非基变量(替入变量)和一个基变量(替初变量),并替换两者的角色。上式变成: 【第二轮旋转】 step 1: 在目标函数里找到一个系数为负的非基变量,作为入基变量 选择 x 2 x_2 x2作为入基变量 step2:将入基变量用基变量表示,准备替换: 常数项除以入基变量系数,第2个式子和最后一个式子除完分别是:2/1=2,6/3=2。 上面第2个式子和最后一个式子中都有 x 2 x_2 x2,我们选择哪个来表示 x 2 x_2 x2呢? 我们来比较一下: 用第2个式子表示 x 2 = 2 − x 3 − x 4 + x 5 x_2 =2-x_3-x_4+x_5 x2=2−x3−x4+x5,相当于 x 2 ≤ 2 x_2 \leq 2 x2≤2( x 3 和 x 5 x_3和x_5 x3和x5都在右边,也就是非基变量,取0, 2 − x 4 ≤ 2 2-x_4 \leq 2 2−x4≤2)。用最后一个式子表示 x 2 = ( 6 − x 3 − x 7 ) / 3 x_2 =(6 -x_3-x_7) / 3 x2=(6−x3−x7)/3,相当于 x 2 ≤ 2 x_2 \leq 2 x2≤2。因此,最后将 x 2 x_2 x2表示成: x 2 = 2 − x 3 − x 4 + x 5 x_2 =2-x_3-x_4+x_5 x2=2−x3−x4+x5。 这里如果用$x_2 =(6 -x_3-x_7) / 3$,最终没有算出来,会得到一个非可行解,为什么。(todo) step 3: 将入基变量的表达式,带入目标函数,完成转动 step4:非基变量变为0,更新基本解和目标函数 新的基本解为(2,2, 0, 0, 0, 3, 0),目标函数 z = − 30 z=-30 z=−30 【第三轮旋转】 step 1: 在目标函数里找到一个系数为负的非基变量,作为入基变量 选择 x 5 x_5 x5作为入基变量,因为只有它的系数为负啦! step2:将入基变量用基变量表示,准备替换: 用约束的常数项除以入基变量的系数,上式2、3、5除完分别是:2,2,0。因此选择最后一个表达式。 上式2、3、5中都有 x 3 x_3 x3,我们到底用哪个来表示呢? 我们来比较一下: 用第2个式子表示: x 5 = x 2 + x 3 + x 4 − 2 x_5=x_2+x_3+x_4-2 x5=x2+x3+x4−2,即无限制;用第3个式子表示: x 5 = 2 − x 1 x_5 =2- x_1 x5=2−x1,即 x 2 ≤ 2 x_2 \leq 2 x2≤2;用第5个式子表示: x 5 = ( 2 x 3 + 3 x 4 − x 7 ) / 3 x_5=(2x_3+3x_4-x_7)/3 x5=(2x3+3x4−x7)/3,即 3 x 5 ≤ 2 x 3 + 3 x 4 3x_5 \leq 2x_3+3x_4 3x5≤2x3+3x4, x 3 x 4 x_3x_4 x3x4都是非基变量,取0, 3 x 5 ≤ 0 3x_5 \leq 0 3x5≤0;理解对吗?(todo)选择约束的最紧的那个 x 5 = ( 2 x 3 + 3 x 4 − x 7 ) / 3 x_5=(2x_3+3x_4-x_7)/3 x5=(2x3+3x4−x7)/3。 step 3: 将入基变量的表达式,带入目标函数,完成转动 新的基本解为(0,1, 3, 0, 2, 0, 0),目标函数 z = − 32 z=-32 z=−32 终止条件就是目标函数中,已经没有系数为负的变量了! 一些badcase 退化所谓退化指的是旋转过程中,目标函数值停在某个值不变了。这是使得单纯形算法不会终止的唯一原因。 解决方法——使用Bland规则: 在选择入基变量和出基变量的时候,总是选择满足条件的下标最小的变量: 入基变量:目标函数中系数为负的下标最小值对应的变量;出基变量:对所有的约束条件中,选择约束条件最紧的那一个。 初始解不是可行解以及无解的情况导致初始解不是可行解的原因: b i b_i bi存在负数! 具体要怎么做,有点复杂,看官直接看大佬的线性规划:单纯形法详解即可。 找不到有限制条件的替入变量——无界解回顾一下线性规划解的4种情况: 唯一最优解;无穷最优解(多重解);无可行解;无界解。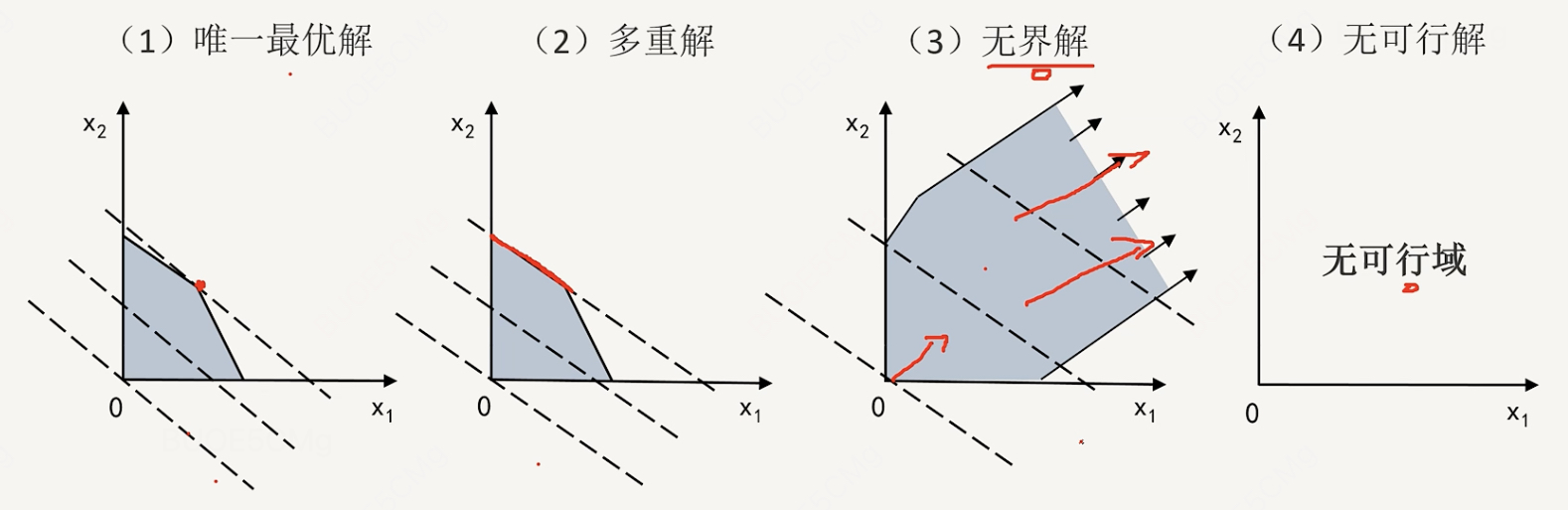
当能找到替入变量,但对替入变量没有任何约束时(找不到替出变量?),说明是无界解的情况。 时间复杂度最坏的情况下是非多项式的(指数时间复杂度,
O
(
2
n
)
O(2^n)
O(2n)),绝大多数情况是多项式时间(
O
(
n
)
O(n)
O(n) ~
O
(
n
3
)
O(n^3)
O(n3))。下图左侧是多项式量级,右边是非多项式量级。 对算法时间复杂度计算感兴趣的,可以参考我的文章:算法时空复杂度分析:大O表示法。 附录 一些基本概念   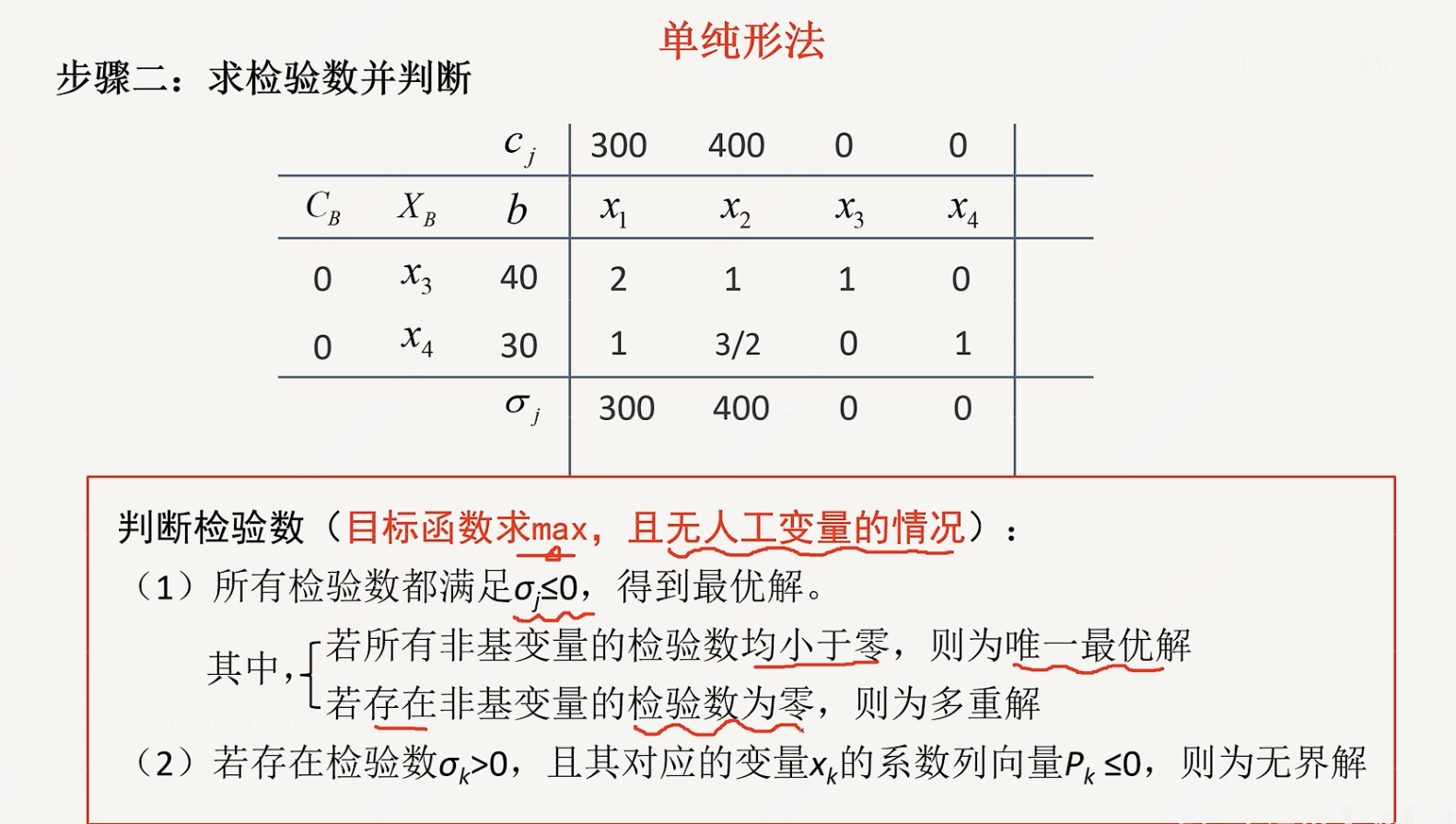 参考资料
线性规划:单纯形法详解《运筹学基础》 李志猛运筹学与单纯形法
参考资料
线性规划:单纯形法详解《运筹学基础》 李志猛运筹学与单纯形法
|
【本文地址】
| 今日新闻 |
| 推荐新闻 |
| 专题文章 |
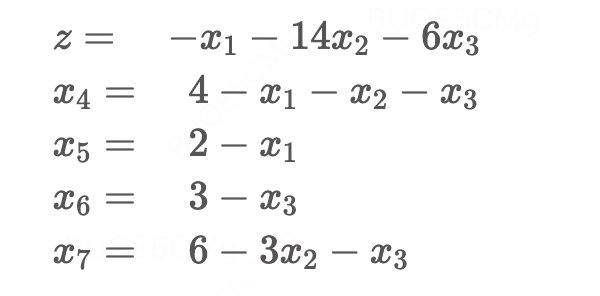
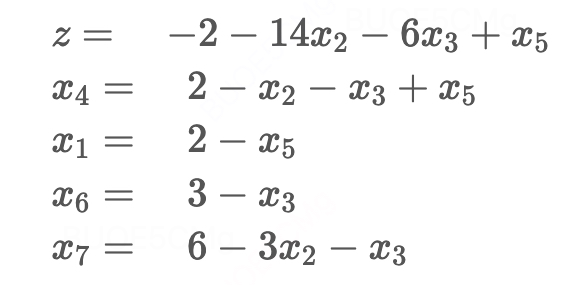 step4:非基变量变为0,更新基本解和目标函数 得到另一个可行解:(2, 0, 0, 2, 0, 3, 6),目标函数值
z
=
−
2
z=-2
z=−2,
step4:非基变量变为0,更新基本解和目标函数 得到另一个可行解:(2, 0, 0, 2, 0, 3, 6),目标函数值
z
=
−
2
z=-2
z=−2,