| 超全面的协方差矩阵介绍 | 您所在的位置:网站首页 › 协方差矩阵符号怎么读 › 超全面的协方差矩阵介绍 |
超全面的协方差矩阵介绍
|
阅读本文需要具备一定的线性代数基础,通过本文,你将对协方差矩阵有全面的理解。  定义
定义
一组随机变量,共n个: X = ( X 1 , X 2 , . . . , X n ) T \mathbf{X}=(X_1,X_2,...,X_n)^T X=(X1,X2,...,Xn)T 两个随机变量的协方差: c o v [ X i , X j ] = E [ ( X i − E [ X i ] ) ( X j − E [ X j ] ) ] cov[X_i,X_j]=E[(X_i-E[X_i])(X_j-E[X_j])] cov[Xi,Xj]=E[(Xi−E[Xi])(Xj−E[Xj])] 由n*n个协方差组成的协方差矩阵 c o v [ X , X ] = [ c o v [ X 1 , X 1 ] c o v [ X 1 , X 2 ] ⋯ c o v [ X 1 , X n ] c o v [ X 2 , X 1 ] c o v [ X 2 , X 2 ] ⋯ c o v [ X 2 , X n ] ⋮ ⋮ ⋱ ⋮ c o v [ X n , X 1 ] c o v [ X n , X 2 ] ⋯ c o v [ X n , X n ] ] cov[\mathbf{X,X}]={\begin{bmatrix} cov[X_1,X_1]& cov[X_1,X_2] & \cdots & cov[X_1,X_n]\\ cov[X_2,X_1] & cov[X_2,X_2] & \cdots & cov[X_2,X_n]\\ \vdots & \vdots & \ddots & \vdots\\ cov[X_n,X_1] & cov[X_n,X_2] & \cdots & cov[X_n,X_n] \end{bmatrix}} cov[X,X]=⎣⎢⎢⎢⎡cov[X1,X1]cov[X2,X1]⋮cov[Xn,X1]cov[X1,X2]cov[X2,X2]⋮cov[Xn,X2]⋯⋯⋱⋯cov[X1,Xn]cov[X2,Xn]⋮cov[Xn,Xn]⎦⎥⎥⎥⎤ 直观理解 协方差表示两个随机变量之间的线性相关性协方差矩阵中的每个元素代表了两个随机变量之间的协方差协方差矩阵表示一组随机变量之间的两两线性相关性 例子图片和示例来源(点击进入图片来源) 有二维随机变量x和y,简便期间,我们对x和y做了去均值处理( x ˉ = y ˉ = 0 \bar x=\bar y = 0 xˉ=yˉ=0),所以x和y之间的协方差: c o v [ x , y ] = E [ ( x − x ˉ ) ( y − y ˉ ) ] = E [ x ⋅ y ] cov[x,y] = E[(x-\bar x)(y-\bar y)]=E[x\cdot y] cov[x,y]=E[(x−xˉ)(y−yˉ)]=E[x⋅y] 如果x和y的联合分布多分布在一三象限, x ⋅ y x\cdot y x⋅y多为正数,则协方差为正,x和y正相关。 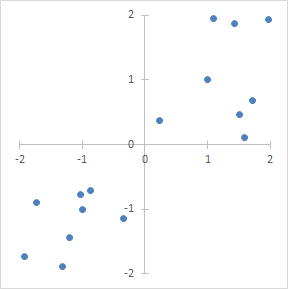
如果x和y的联合分布多分布在二四象限, x ⋅ y x\cdot y x⋅y多为负数,则协方差为负,x和y负相关。 
如果x和y的几乎均匀地分散在所有象限中,则 x ⋅ y x\cdot y x⋅y有正有负,均值接近于0,说明x和y之间没有相关性(只是说没有线性相关)。 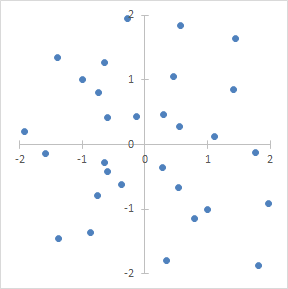 线性相关与非线性相关
线性相关与非线性相关
若两个向量的协方差为0,则两个向量不具备线性相关性,但它们仍然可能不独立,因为可能存在非线性的相关性。 具体的,协方差为0但不独立的原因在于:随机向量x和随机向量y之间的关系没有一阶分量,只有二阶或高阶分量(关于一阶分量、二级分量等详见泰勒公式)。 举个例子(来自知乎匿名用户):对于随机变量x和随机变量y,有 x 2 + y 2 = 1 x^2+y^2=1 x2+y2=1,其几何关系如下图:  性质
协方差矩阵是半正定矩阵
性质
协方差矩阵是半正定矩阵
半正定矩阵的定义: 设A是实对称矩阵。如果对任意的实非零列向量x有 x T A x ≥ 0 x^TAx≥0 xTAx≥0,就称A为半正定矩阵。 半正定矩阵的性质: 半正定矩阵的行列式是非负的半正定矩阵的特征值都是非负的…延伸: 实对称矩阵一定是半正定矩阵 证明:协方差矩阵是半正定的 对任意向量y: y T Σ y = y T E [ ( X − μ ) ( X − μ ) T ] y = E [ y T ( X − μ ) ( X − μ ) T y ] = E [ ( ( X − μ ) T y ) T ( ( x − μ ) T y ) ] = E [ ∣ ∣ ( X − μ ) T y ∣ ∣ 2 ] ≥ 0 y^T\Sigma y = y^TE[(X-\mu)(X-\mu)^T]y \\ \ \ \ \ \ \ \ \ \ \ \ =E[y^T(X-\mu)(X-\mu)^Ty] \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =E[((X-\mu)^Ty)^T((x-\mu)^Ty)] \\ \ \ \ \ \ =E[||(X-\mu)^Ty||^2] \geq 0 yTΣy=yTE[(X−μ)(X−μ)T]y =E[yT(X−μ)(X−μ)Ty] =E[((X−μ)Ty)T((x−μ)Ty)] =E[∣∣(X−μ)Ty∣∣2]≥0 正定矩阵的定义: A是n阶方阵,如果对任何非零向量x,都有 x T A x > 0 x^TAx>0 xTAx>0,其中 x T x^T xT 表示x的转置,就称A正定矩阵 正定矩阵的性质: 正定矩阵的行列式恒为正正定矩阵的特征值均为正… 协方差矩阵是实对称矩阵实对称矩阵的性质: 实对称矩阵的不同特征值对应的特征向量时正交的实对称矩阵的特征值是实数,特征向量是实向量实对称矩阵必可对角化,且其相似对角矩阵的对角线元素为n个特征值实对称矩阵的对角化: P − 1 A P = P − 1 P ∧ = ∧ P^{-1}AP = P^{-1}P \wedge=\wedge P−1AP=P−1P∧=∧ 其中对角矩阵 ∧ \wedge ∧的对角元素为矩阵A的n个特征值(n个特征值中可能重复的),P由矩阵A的特征向量组成。 与其他统计量的关系与协方差的关系: 协方差矩阵的第i行第j列的元素是第i个随机向量和第j个随机向量之间的协方差从协方差到协方差矩阵是从标量随机变量到高维随机向量的推广与相关系数矩阵的关系: 相关系数矩阵为 c o r r ( X ) corr(\mathbf{X}) corr(X) corr ( X ) = ( diag ( c o v ( X X ) ) ) − 1 2 c o v ( X X ) ( diag ( c o v ( X X ) ) ) − 1 2 {\displaystyle \operatorname {corr} (\mathbf {X} )={\big (}\operatorname {diag} (cov({\mathbf {X} \mathbf {X} })){\big )}^{-{\frac {1}{2}}}\,cov({\mathbf {X} \mathbf {X}) }\,{\big (}\operatorname {diag} (cov({\mathbf {X} \mathbf {X}) }){\big )}^{-{\frac {1}{2}}}} corr(X)=(diag(cov(XX)))−21cov(XX)(diag(cov(XX)))−21 延伸:PCA中对协方差矩阵的应用详见《图文并茂的PCA教程》 Python实战 import numpy as np x = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9]) y = np.array([9, 8, 7, 6, 5, 4, 3, 2, 1]) Sigma = np.cov(x, y) print(Sigma) '''输出: [[ 7.5 -7.5] [-7.5 7.5]] ''' |
【本文地址】