| 对SLAM系统中的协方差矩阵与信息矩阵，以及舒尔补和边缘化的理解 | 您所在的位置：网站首页 › 协方差矩阵为0 › 对SLAM系统中的协方差矩阵与信息矩阵，以及舒尔补和边缘化的理解 |
对SLAM系统中的协方差矩阵与信息矩阵，以及舒尔补和边缘化的理解
|
首先关于什么是协方差矩阵与信息矩阵。 在零均值的多元高斯分布中有如下概率形式： p ( x ) = 1 Z e x p ( − 1 2 x ⊤ Σ − 1 x ) p(x)={1\over Z}exp(-{1\over 2}x^⊤Σ^{−1}x) p(x)=Z1exp(−21x⊤Σ−1x)其中 Σ Σ Σ为协方差矩阵，而协方差矩阵的逆 Λ = Σ − 1 Λ = Σ−1 Λ=Σ−1则为信息矩阵。比如在 X X X为三维变量时，协方差矩阵 Σ i j = E ( x i x j ) Σ_{ij}=E(x_ix_j) Σij=E(xixj)为对应元素求期望。 样例：
v
i
v_i
vi相互独立，且各自服从协方差为
σ
i
2
\sigma^2_i
σi2的高斯分布。 |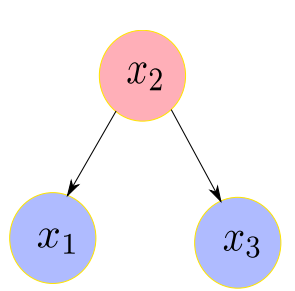
根据协方差的计算公式
Σ
i
j
=
E
(
x
i
x
j
)
Σ_{ij}=E(x_ix_j)
Σij=E(xixj)，可求解得到：
Σ
11
=
E
(
x
1
x
1
)
=
E
(
w
1
v
2
+
v
1
)
(
w
1
v
2
+
v
1
)
=
w
1
2
E
(
v
2
2
)
+
2
w
1
E
(
v
1
v
2
)
+
E
(
v
1
2
)
=
w
1
2
σ
2
2
+
σ
1
2
Σ_{11}=E(x_1x_1)=E(w_1v_2+v_1)(w_1v_2+v_1) \\ =w_1^2E(v^2_2)+2w_1E(v_1v_2)+E(v_1^2) \\ =w^2_1 \sigma^2_2+\sigma^2_1
Σ11=E(x1x1)=E(w1v2+v1)(w1v2+v1)=w12E(v22)+2w1E(v1v2)+E(v12)=w12σ22+σ12同理可得到整个协方差矩阵：
Σ
=
[
w
1
2
σ
2
2
+
σ
1
2
w
1
σ
2
2
w
1
w
3
σ
2
2
w
1
σ
2
2
σ
2
2
w
3
σ
2
2
w
1
w
3
σ
2
2
w
3
σ
2
2
w
3
2
σ
2
2
+
σ
3
2
]
Σ=\begin{bmatrix} w^2_1 \sigma^2_2+\sigma^2_1 & w_1\sigma^2_2 & w_1w_3\sigma^2_2 \\ w_1\sigma^2_2 & \sigma_2^2 & w_3\sigma^2_2 \\ w_1w_3\sigma^2_2 & w_3\sigma^2_2 & w_3^2\sigma^2_2+\sigma^2_3\\ \end{bmatrix}
Σ=⎣⎡w12σ22+σ12w1σ22w1w3σ22w1σ22σ22w3σ22w1w3σ22w3σ22w32σ22+σ32⎦⎤其信息矩阵的求解等于它的逆，直接求解较为困难，这里通过联合高斯分布计算得到协方差的逆。
p
(
x
1
,
x
2
,
x
3
)
=
p
(
x
2
)
p
(
x
1
∣
x
2
)
p
(
x
3
∣
x
2
)
p(x_1,x_2,x_3)=p(x_2)p(x_1|x_2)p(x_3|x_2)
p(x1,x2,x3)=p(x2)p(x1∣x2)p(x3∣x2)带入如下形式：
p
(
x
)
=
1
Z
e
x
p
(
−
1
2
x
⊤
Σ
−
1
x
)
p(x)={1\over Z}exp(-{1\over 2}x^⊤Σ^{−1}x)
p(x)=Z1exp(−21x⊤Σ−1x)
p
(
x
1
,
x
2
,
x
3
)
=
1
Z
1
e
x
p
(
−
x
2
2
2
σ
2
2
)
1
Z
e
x
p
(
−
(
x
1
−
w
1
x
2
)
2
2
σ
1
2
)
1
Z
e
x
p
(
−
(
x
3
−
w
3
x
2
)
2
σ
3
2
)
=
1
2
e
x
p
(
−
1
2
[
x
1
x
2
x
3
]
[
1
σ
1
2
−
w
1
σ
1
2
0
−
w
1
σ
1
2
w
1
2
σ
1
2
+
1
σ
2
2
+
w
3
2
σ
1
2
−
w
3
σ
3
2
0
w
3
σ
3
2
1
σ
3
2
]
[
x
1
x
2
x
3
]
)
=
1
Z
e
x
p
(
−
1
2
x
⊤
Σ
−
1
x
)
p(x_1,x_2,x_3)={\color{green}{1\over Z_1}exp(-{x_2^2\over 2\sigma^2_2})}{\color{red}{1\over Z}exp(-{(x_1-w_1x_2)^2\over 2\sigma_1^2})}{\color{blue}{1\over Z}exp(-{(x_3-w_3x_2)^2\over \sigma_3^2})} \\ ={1\over 2}exp(-{1\over 2} \begin{bmatrix} x_1 & x_2 & x_3\\ \end{bmatrix} \begin{bmatrix} {\color{red}{1\over \sigma_1^2} }& {\color{red}-{w_1\over \sigma_1^2} }& 0 \\{\color{red} -{w_1\over \sigma_1^2}} & {\color{red}{w^2_1\over \sigma_1^2}}+{\color{green}{1\over \sigma_2^2}}+{\color{blue}{w^2_3\over \sigma_1^2}} &{\color{blue} -{w_3\over \sigma_3^2} }\\ 0 & {\color{blue}{w_3\over \sigma_3^2} }& {\color{blue}{1\over \sigma_3^2}}\\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3\\ \end{bmatrix} ) \\ ={1\over Z}exp(-{1\over 2}x^⊤Σ^{−1}x)
p(x1,x2,x3)=Z11exp(−2σ22x22)Z1exp(−2σ12(x1−w1x2)2)Z1exp(−σ32(x3−w3x2)2)=21exp(−21[x1x2x3]⎣⎢⎡σ121−σ12w10−σ12w1σ12w12+σ221+σ12w32σ32w30−σ32w3σ321⎦⎥⎤⎣⎡x1x2x3⎦⎤)=Z1exp(−21x⊤Σ−1x)由此得到协方差矩阵的逆：
Σ
−
1
Σ^{−1}
Σ−1，即信息矩阵。 协方差逆矩阵中如果坐标为
(
i
,
j
)
(i, j)
(i,j)的元素为 0，表示元素
i
i
i 和
j
j
j在其他变量固定的情况下条件独立。协方差中非对角元素
Σ
i
j
>
0
Σ_{ij}>0
Σij>0表示俩变量正相关，而在信息矩阵
Λ
i
j
<
0
Λ_{ij}【本文地址】