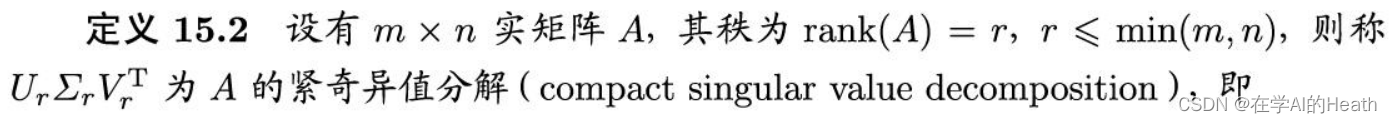降维算法之奇异值分解SVD：7000字长文，看这一篇就够了！

您所在的位置：网站首页 › 分解题目图片 › 降维算法之奇异值分解SVD：7000字长文，看这一篇就够了！

降维算法之奇异值分解SVD：7000字长文，看这一篇就够了！

2024-05-31 21:09| 来源: 网络整理| 查看: 265

引言

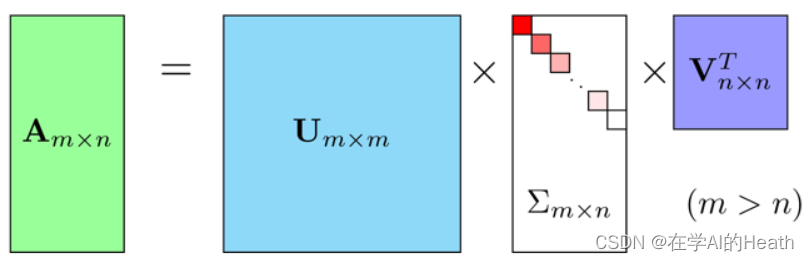
在2006年，Netflix曾经举办了一个奖金为100万美元的推荐系统算法比赛，最后的获奖者就使用了矩阵分解中的明星：奇异值分解SVD。SVD被广泛应用在推荐系统、图像处理等领域，是一种数据降维的经典方法。降维属于特征提取的子任务，关于降维，可以参考这篇博客。

在正式阅读本文之前，不妨先看一个Youtube上Serrano Academic解释SVD的视频，再来阅读本文：这是他的B站视频&Youtube视频，可以很好地解释SVD的性质。

太长不看版：奇异值分解的通俗解释

许多数学对象可以通过将它们分解成多个组成部分或者找到它们的一些属性来更好地理解，这些属性是通用的,而不是由我们选择它们的方式所产生的。

例如，我们可以通过分解质因数来发现整数的一些内在性质。尽管我们可以用十进制或者二进制等不同方式表示整数12.但是12=2×3×3总是对的。从这个表示中我们可以获得一些有用的信息，比如12不能被5整除，或者12的倍数能够被3整除。

对应地，我们也可以通过分解矩阵来发现矩阵表示成数组元素时不明显的函数性质。特征分解是使用最广的矩阵分解之一，在这个分解中，我们将矩阵分解成一组特征向量和特征值。这样可以帮助我们分析矩阵的特定性质，就像质因数分解有助于我们理解整数。

奇异值分解是将矩阵分解为奇异向量和奇异值。通过奇异值分解，我们会得到一些与特征分解相同类型的信息。然而，奇异值分解有更广泛的应用。每一个实数矩阵都有一个奇异值分解，但不一定都有特征分解（例如非方阵矩阵）。

例如对于一个矩阵 $\boldsymbol{A}$ ，我们使用特征分解去分析矩阵 $\boldsymbol{A}$ 时，会得到特征向量构成的矩阵 $\boldsymbol{V}$ 和特征值构成的向量 $\boldsymbol{\lambda}$ ，我们可以重新将 $\boldsymbol{A}$ 写作：

$\boldsymbol{A}=\boldsymbol{V}\mathrm{diag}\left( \boldsymbol{\lambda } \right) \boldsymbol{V}^{-\boldsymbol{1}}$

奇异值分解是类似的，只不过这回我们将矩阵 $\boldsymbol{A}$ 分解成三个矩阵的乘积：

$\boldsymbol{A}\,\,=\,\,\boldsymbol{U\varSigma V}^{\boldsymbol{T}}$

其中， $\boldsymbol{U}$ 是 $m$ 阶正交矩阵， $\boldsymbol{V}$ 是 $n$ 阶正交矩阵， $\boldsymbol{\varSigma }$ 是由降序排列的非负的对角线元素组成的 $m\times n$ 矩形对角矩阵（不一定是方阵），对角线上的元素就叫做奇异值，既是 $\boldsymbol{A}^T\boldsymbol{A}$ 特征值的平方根，也是 $\boldsymbol{AA}^T$ 特征值的平方根。 $\boldsymbol{U\varSigma V}^{\boldsymbol{T}}$ 称为矩阵 $\boldsymbol{A}$ 的奇异值分解， $\boldsymbol{U}$ 的列向量被称为左奇异向量，是 $\boldsymbol{AA}^T$ 的特征向量； $\boldsymbol{V}$ 的列向量被称为右奇异向量，是 $\boldsymbol{A}^T\boldsymbol{A}$ 的特征向量。

太长不看版：奇异值分解的通俗解释

一、奇异值分解的定义与性质

1.1 奇异值分解简介

1.2 奇异值分解的定义和定理

1.3 奇异值分解的实例及numpy代码实现

1.4 最有用的性质：Moore-Penrose 伪逆

二、紧奇异值分解和截断奇异值分解

2.1 紧奇异值分解

2.2 截断奇异值分解

2.3 截断奇异值分解的numpy代码实现

三、奇异值分解的几何解释

四、如何理解“奇异值分解是在平方损失意义下对矩阵的最优近似”？

4.1 范数及最优近似

4.2 矩阵的外积展开式

4.3 举个例子

五、截断奇异值分解在sklearn中的体现

5.1 使用SVD进行简单矩阵降维并计算可解释方差比例

5.2 使用完全随机树的哈希特征转换

5.3 手写数字识别的嵌入（embedding）表示

六、如何使用奇异值分解进行图像压缩？

七、奇异值分解在推荐系统中的应用

扩展阅读

一、奇异值分解的定义与性质 1.1 奇异值分解简介

奇异值分解（singular value decomposition,SVD）是一种矩阵因子分解方法，是线性代数的概念，但在机器学习中被广泛应用。奇异值分解将任何给定矩阵分解为三个矩阵的乘积：一个正交的左奇异向量矩阵、一个对角的奇异值矩阵和一个正交的右奇异向量矩阵。将数据集的奇异值表征按重要性排列，舍弃不重要的特征向量，达到降维的目的，从而找出数据中的主成分。矩阵的奇异值分解可以看做是矩阵数据压缩的一种方法，即用因子分解的方式近似地表示原始矩阵，这种近似是在平方损失意义下的最优近似。它在应用如数据降维、信息检索、信号处理和图像压缩等领域具有重要作用。

1.2 奇异值分解的定义和定理

矩阵的奇异值分解是指将一个非零的实矩阵 $\boldsymbol{A}$ ， $\boldsymbol{A}\,\,\epsilon \,\,\boldsymbol{R}^{m\times n}$ ，表示为以下三个实矩阵乘积形式的运算，即进行矩阵的因子分解：

$\boldsymbol{A}\,\,=\,\,\boldsymbol{U\varSigma V}^{\boldsymbol{T}}$

其中， $\boldsymbol{U}$ 是 $m$ 阶正交矩阵， $\boldsymbol{V}$ 是 $n$ 阶正交矩阵， $\boldsymbol{\varSigma }$ 是由降序排列的非负的对角线元素组成的 $m\times n$ 矩形对角矩阵，对角线上的元素就叫做奇异值，满足：

$\\ \boldsymbol{UU}^{\boldsymbol{T}}=\boldsymbol{I} \\ \boldsymbol{VV}^{\boldsymbol{T}}=\boldsymbol{I} \\ \boldsymbol{\varSigma }=\mathrm{diag}\left( \boldsymbol{\sigma }_1,\boldsymbol{\sigma }_2\cdots \boldsymbol{\sigma }_{\boldsymbol{p}} \right) \\ \boldsymbol{\sigma }_1\geqslant \boldsymbol{\sigma }_2\geqslant \cdots \geqslant \boldsymbol{\sigma }_{\boldsymbol{p}}\geqslant 0 \\ \boldsymbol{p}=\boldsymbol{min}\left( \boldsymbol{m},\boldsymbol{n} \right) \\$

$\boldsymbol{U\varSigma V}^{\boldsymbol{T}}$ 称为矩阵 $\boldsymbol{A}$ 的奇异值分解， $\boldsymbol{\sigma }_{\boldsymbol{i}}$ 称为矩阵 $\boldsymbol{A}$ 的奇异值， $\boldsymbol{U}$ 的列向量被称为左奇异向量， $\boldsymbol{V}$ 的列向量被称为右奇异向量。

任意给定一个实矩阵，其奇异值分解一定存在，但不唯一，这就是奇异值分解的基本定理。

1.3 奇异值分解的实例及numpy代码实现

奇异值分解的直观表现如下图所示：

例如一个5×4的矩阵 $\boldsymbol{A}$ 要进行奇异值分解，则 $\boldsymbol{A}$ 的奇异值分解可表示为：

$\boldsymbol{A}_{5\times 4}=\boldsymbol{U}_{5\times 5}\boldsymbol{\varSigma }_{5\times 4}\boldsymbol{V}_{4\times 4}$

给定矩阵 $\boldsymbol{A}$ ：

$\boldsymbol{A}_{5\times 4}=\left[ \begin{array}{c} \begin{matrix} 1& 0& 0& 0\\ 0& 0& 0& 4\\ 0& 3& 0& 0\\ 0& 0& 0& 0\\ \end{matrix}\\ \begin{matrix} 2& 0& 0& 0\\ \end{matrix}\\ \end{array} \right]$

它的奇异值分解由三个矩阵的乘积 $\boldsymbol{U\varSigma V}^{\boldsymbol{T}}$ ，矩阵 $\boldsymbol{U}$ ， $\boldsymbol{\varSigma }$ ， $\boldsymbol{V}$ 分别为：

$\boldsymbol{U}_{5\times 5}=\left[ \begin{array}{c} \begin{matrix} 0& 0& \sqrt{0.2}& 0\\ 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\\ \end{matrix}\begin{array}{c} \sqrt{0.8}\\ 0\\ 0\\ 0\\ \end{array}\\ \begin{matrix} \begin{matrix} 0& 0\\ \end{matrix}& \sqrt{0.8}& 0& -\sqrt{0.2}\\ \end{matrix}\\ \end{array} \right]$

$\boldsymbol{\varSigma }_{5\times 4}=\left[ \begin{array}{c} \begin{matrix} 4& 0& 0& 0\\ 0& 3& 0& 0\\ 0& 0& \sqrt{5}& 0\\ 0& 0& 0& 0\\ \end{matrix}\\ \begin{matrix} 2& 0& \,\,0& \,\,0\\ \end{matrix}\\ \end{array} \right]$ $\boldsymbol{V}_{4\times 4}=\left[ \begin{matrix} 0& 0& 0& 1\\ 0& 1& 0& 0\\ 1& 0& 0& 0\\ 0& 0& 1& 0\\ \end{matrix} \right]$

矩阵 $\boldsymbol{\varSigma }_{5\times 4}$ 是对角矩阵，对角线外的元素都是0，对角线上元素非负，按降序排列。矩阵 $\boldsymbol{U}_{5\times 5}$ 和 $\boldsymbol{V}_{4\times 4}$ 是正交矩阵，它们与各自的转置矩阵相乘是单位矩阵 $\boldsymbol{I}$ 。

矩阵的奇异值分解并不唯一，如果在此例中选择U为

而 $\boldsymbol{\varSigma }_{5\times 4}$ 和 $\boldsymbol{V}_{4\times 4}$ 不变，那么 $\boldsymbol{U\varSigma V}^{\boldsymbol{T}}$ 也是 $\boldsymbol{A}$ 的一个奇异值分解。

使用numpy进行上述矩阵的奇异值分解代码如下：

import numpy as np # 创建矩阵A A = np.array([[1, 0, 0, 0], [0, 0, 0, 4], [0, 3, 0, 0], [0, 0, 0, 0], [2, 0, 0, 0]]) # 进行奇异值分解 U, s, V = np.linalg.svd(A) # 打印结果 print("U:\n", U) print("s:", s) print("V:\n", V)

运行结果如下：

U: [[ 0. 0. -0.4472136 0. -0.89442719] [-1. 0. 0. 0. 0. ] [ 0. -1. 0. 0. 0. ] [ 0. 0. 0. 1. 0. ] [ 0. 0. -0.89442719 0. 0.4472136 ]] s: [ 4. 3. 2.23606798 -0. ] V: [[-0. -0. -0. -1.] [-0. -1. -0. -0.] [-1. -0. -0. -0.] [-0. -0. -1. -0.]] 1.4 最有用的性质：Moore-Penrose 伪逆

SVD的一个最有用的性质可能是拓展矩阵求逆到非方的矩阵上。Moore-Penrose 伪逆使我们在求解非方矩阵的线性方程中取得了一定的进展。矩阵 $\boldsymbol{A}$ 的伪逆定义为：

$\boldsymbol{A}^+=\underset{a\rightarrow 0}{\lim}\left( \boldsymbol{A}^T\boldsymbol{A}+\alpha I \right) ^{-1}\boldsymbol{A}^T$

计算伪逆的式计算法并没有基于这个定义，而是使用下面的公式

$\boldsymbol{A}^+=\boldsymbol{V\varSigma }^+\boldsymbol{U}^T$

其中 $\boldsymbol{V}$ 、 $\boldsymbol{\varSigma}$ 、 $\boldsymbol{U}$ 是矩阵 $\boldsymbol{A}$ 奇异值分解后得到的矩阵。对角矩阵 $\boldsymbol{\varSigma }$ 的伪逆 $\boldsymbol{\varSigma }^+$ 是其非零元素取倒数之后再转置得到的。当矩阵 $\boldsymbol{A}$ 的列数多于行数时，使用伪逆求解线性方程是众多可能解法中的一种，行数多于列数时，可能没有解。

二、紧奇异值分解和截断奇异值分解

1.3中提到的奇异值分解被称为矩阵的完全奇异值分解。实际上常用的是奇异值分解的紧凑形式和截断形式。紧奇异值分解是与原始矩阵等秩的奇异值分解，截断奇异值分解是比原始矩阵低秩的奇异值分解。

2.1 紧奇异值分解

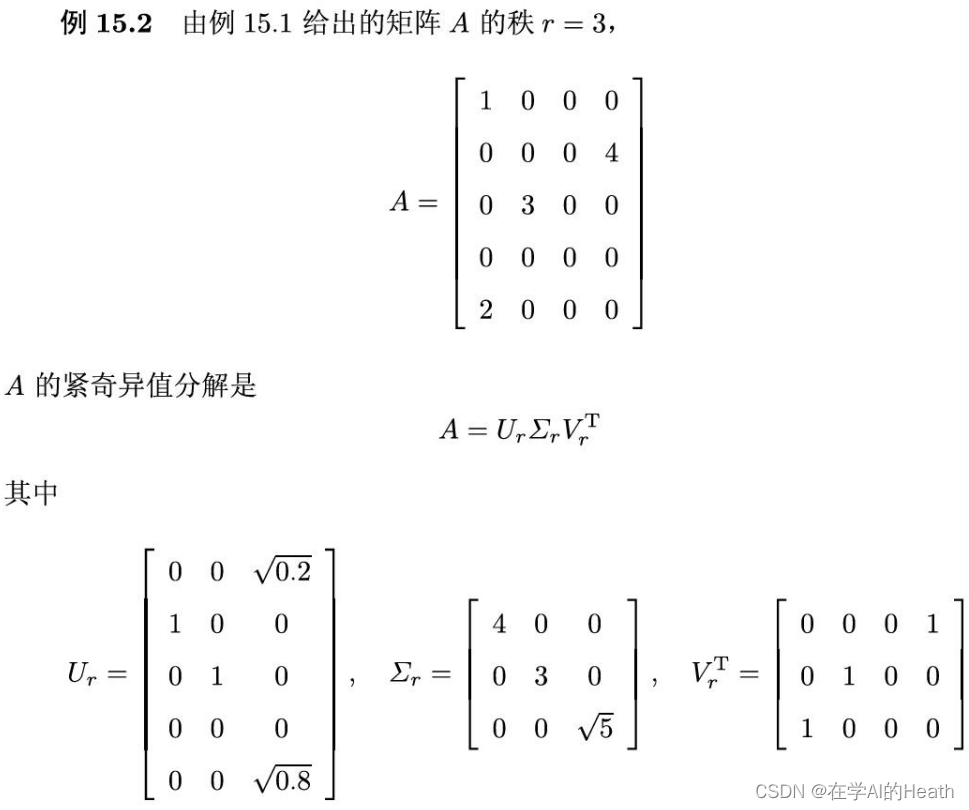
紧奇异值分解的举例，还是上面那个例子：

2.2 截断奇异值分解

在矩阵的奇异值分解中，只取最大的k个奇异值（k

【本文地址】

公司简介

联系我们