一般迭代法（一）

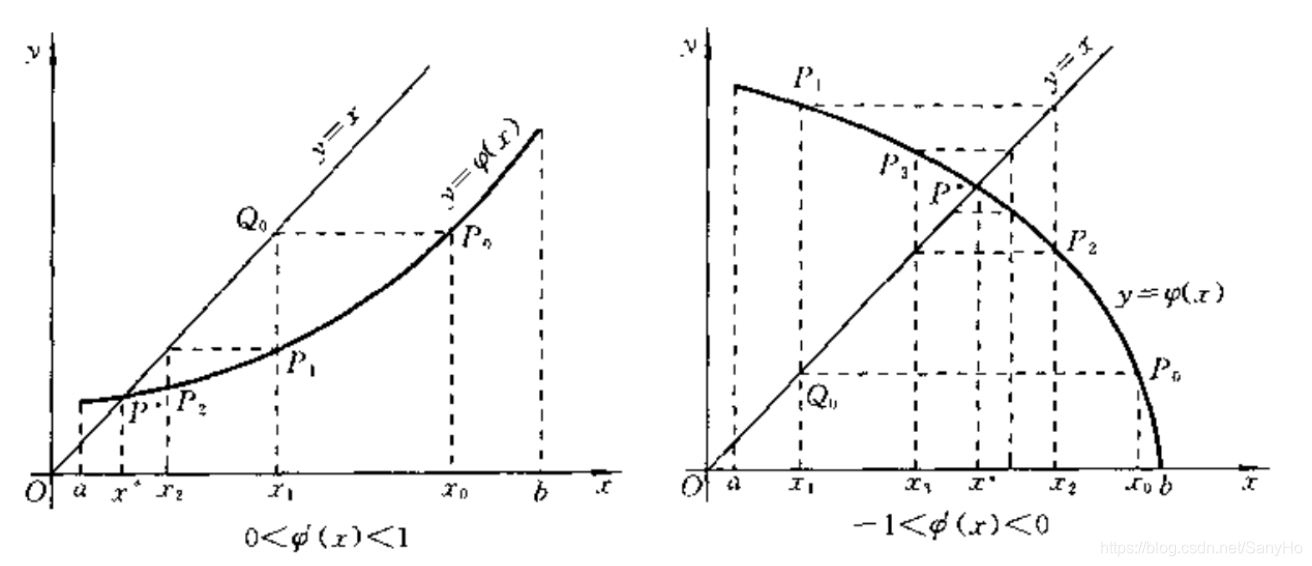
先看一个例子。设有两个函数 y = φ ( x ) y=\varphi(x) y=φ(x)和 y = x y=x y=x，欲求其交点 x ∗ x^* x∗。为此，可将函数 y = x y=x y=x改写成 x = y x=y x=y的形式，并给定一个初始值 x 0 x_0 x0​，并进行如下计算：

（1）先计算函数 y = φ ( x ) y=\varphi(x) y=φ(x)在 x 0 x_0 x0​处的函数值 y 0 y_0 y0​，然后计算函数 x = y x=y x=y在 y 0 y_0 y0​处的值 x 1 x_1 x1​，即： y 0 = φ ( x 0 ) , x 1 = y 0 y_0=\varphi(x_0), \quad x_1=y_0 y0​=φ(x0​),x1​=y0​ 通过上述变换规则，由 x 0 x_0 x0​得到 x 1 x_1 x1​， x 1 x_1 x1​一般不同于 x 0 x_0 x0​，并且由 x 0 x_0 x0​惟一确定。

（2）再计算函数 y = φ ( x ) y=\varphi(x) y=φ(x)在 x 1 x_1 x1​处的函数值 y 1 y_1 y1​，然后计算函数 x = y x=y x=y在 y 1 y_1 y1​处的值 x 2 x_2 x2​，即： y 1 = φ ( x 1 ) , x 2 = y 1 y_1=\varphi(x_1),\quad x_2=y_1 y1​=φ(x1​),x2​=y1​ 通过变换规则，由 x 1 x_1 x1​得到 x 2 x_2 x2​， x 2 x_2 x2​不同于 x 1 x_1 x1​并且由 x 1 x_1 x1​惟一确定。

（3）这样一直计算下去，就有可能会得到这样的结果：计算函数 y = φ ( x ) y=\varphi(x) y=φ(x)在 x ∗ x^* x∗处的函数值 y ∗ y^* y∗，然后在计算函数 x = y x=y x=y在 y ∗ y^* y∗处的值时，得到的结果就是 x ∗ x^* x∗，即： y ∗ = φ ( x ∗ ) , x ∗ = y ∗ y^*=\varphi(x^*),\quad x^*=y^* y∗=φ(x∗),x∗=y∗ 即通过同样的变换规则，由 x ∗ x^* x∗得到的仍然是 x ∗ x^* x∗，并且该结果不再改变， x ∗ x^* x∗被称为不动点。上述按某种规则进行变换而得到某个数列 { x 0 , x 1 , x 2 , ⋯   , x ∗ , ⋯   } \{x_0,x_1,x_2,\cdots,x^*,\cdots\} {x0​,x1​,x2​,⋯,x∗,⋯}的过程称为迭代过程。即： x k + 1 = φ ( x k ) , ( k = 0 , 1 , 2 , ⋯   ) x_{k+1}=\varphi(x_k),\quad (k=0,1,2,\cdots) xk+1​=φ(xk​),(k=0,1,2,⋯) 在上述迭代计算过程中，如果数列 { x 0 , x 1 , x 2 , ⋯   , x ∗ , ⋯   } \{x_0,x_1,x_2,\cdots,x^*,\cdots\} {x0​,x1​,x2​,⋯,x∗,⋯}能趋向与某个极限值 x ∗ x^* x∗，则这个极限值必然是函数 y = φ ( x ) y=\varphi(x) y=φ(x)和 x = y x=y x=y的交点 x ∗ x^* x∗，或者是方程组 y = φ ( x ) y=\varphi(x) y=φ(x)和 x = y x=y x=y的解。于是，就得到了一种解方程的数值方法——迭代方法。下图从几何上描述了迭代的具体过程。

一般地，如果将方程组 y = φ ( x ) y=\varphi(x) y=φ(x)和 y = x y=x y=x消去y，则得到一个关于x的方程： x = φ ( x ) x − φ ( x ) = 0 f ( x ) = 0 x=\varphi(x) \\x-\varphi(x)=0 \\f(x)=0 x=φ(x)x−φ(x)=0f(x)=0

在方程 f ( x ) = 0 f(x)=0 f(x)=0中，两个函数的交点 x ∗ x^* x∗必定满足 f ( x ∗ ) = 0 f(x^*)=0 f(x∗)=0，即 f ( x ) = 0 f(x)=0 f(x)=0和方程组 y = φ ( x ) y=\varphi(x) y=φ(x)和 y = x y=x y=x同解。根据这一思路，上溯推导，就可得到方程 f ( x ) = 0 f(x)=0 f(x)=0迭代求根的一般方法。即对一个方程 f ( x ) = 0 f(x)=0 f(x)=0 进行等价变换，只要将其改写为隐式方程形式 x = φ ( x ) (1) x=\varphi(x) \tag{1} x=φ(x)(1) 就得到迭代的计算公式。并且，称 φ ( x ) \varphi(x) φ(x)为迭代函数（1）式一般迭代公式。由于 φ ( x ) \varphi(x) φ(x)中仍然含有未知数x，故方程（1）不能直接求解。如果给出一个迭代初值 x 0 x_0 x0​，则隐式方程（1）可转化为显示方程： x 1 = φ ( x 0 ) x_1=\varphi(x_0) x1​=φ(x0​) 这样，就可以导出一般迭代的格式： x k + 1 = φ ( x k ) , k = 0 , 1 , 2 , ⋯ (2) x_{k+1}=\varphi(x_k),k=0,1,2,\cdots \quad \tag{2} xk+1​=φ(xk​),k=0,1,2,⋯(2) 对于给定的迭代初值 x 0 x_0 x0​，按迭代格式（2）反复计算，将得到一个序列 x 0 , x 1 , x 2 , ⋯   , x k x_0,x_1,x_2,\cdots,x_k x0​,x1​,x2​,⋯,xk​。当 k → ∞ k\to \infty k→∞，如果极限 l i m k → ∞ x k lim_{k\to \infty}x_k limk→∞​xk​存在，则称该迭代格式 x k + 1 = φ ( x k ) x_{k+1}=\varphi(x_k) xk+1​=φ(xk​)是收敛的，并且，该极限就是方程 f ( x ) = 0 f(x)=0 f(x)=0的根，否则称该迭代格式 x k + 1 = φ ( x k ) x_{k+1}=\varphi(x_k) xk+1​=φ(xk​)是发散的。

例1：求方程 x 3 − x − 1 = 0 x^3-x-1=0 x3−x−1=0在 x = 1.5 x=1.5 x=1.5附近的一个根

解：可以将原方程改写为 x = x + 1 x=\sqrt{x+1} x=x+1 ​的形式。由此，可写出一般迭代格式为： x k + 1 = x k + 1 3 , k = 0 , 1 , 2 , ⋯ x_{k+1}= \sqrt[3]{x_k+1},\quad k=0,1,2,\cdots xk+1​=3xk​+1 ​,k=0,1,2,⋯ 取迭代初值 x 0 = 1.5 x_0=1.5 x0​=1.5，按照上述迭代格式进行初次迭代，得到 x 1 = x 0 + 1 3 = 1.35721 x_1=\sqrt[3]{x_0+1}=1.35721 x1​=3x0​+1 ​=1.35721，继续迭代下去，直到第7次和第8次迭代结果分别是 x 7 = 1.32472 x_7=1.32472 x7​=1.32472和 x 8 = 1.32472 x_8=1.32472 x8​=1.32472，两次迭代结果相同，便得到所求的根 x ∗ = 1.32472 x^*=1.32472 x∗=1.32472。下表列出了各次迭代的结果

在使用一般迭代法的过程中，迭代计算结果并不总是收敛的。如果将上述例题所给的方程改写为 x = x 3 − 1 x=x^3-1 x=x3−1，其迭代格式为 x k + 1 = x k 3 − 1 x_{k+1}=x_k^3-1 xk+1​=xk3​−1。若迭代初值仍取 x n = 1.5 x_n=1.5 xn​=1.5，则 x 1 = 2.375 , x 2 = 12.3976 , ⋯   , x_1=2.375,x_2=12.3976,\cdots, x1​=2.375,x2​=12.3976,⋯,这样继续迭代下去，显然得不到正确的结果，即当 k → ∞ k\to\infty k→∞时不会趋于某个极限。这种迭代过程是发散的，而发生的迭代过程是毫无意义的。

下图给出了迭代发散过程的图解 ∣ φ ′ ( x ) ∣ > 1 |\varphi'(x)|>1 ∣φ′(x)∣>1时。因此，在使用一般迭代法时，必须首先检验迭代格式的收敛性。

定理1：设函数 φ ( x ) \varphi(x) φ(x)在 [ a , b ] [a,b] [a,b]上具有连续的一阶导数，且满足条件：

（1）对所有的 x ∈ [ a , b ] x\in[a,b] x∈[a,b]，有 φ ( x ) ∈ [ a , b ] \varphi(x)\in[a,b] φ(x)∈[a,b]

（2）存在 0 < L < 1 0