| 高数随手记：反常积分的收敛和扩散 | 您所在的位置：网站首页 › 函数有收敛的概念吗为什么 › 高数随手记：反常积分的收敛和扩散 |
高数随手记：反常积分的收敛和扩散
概念理解
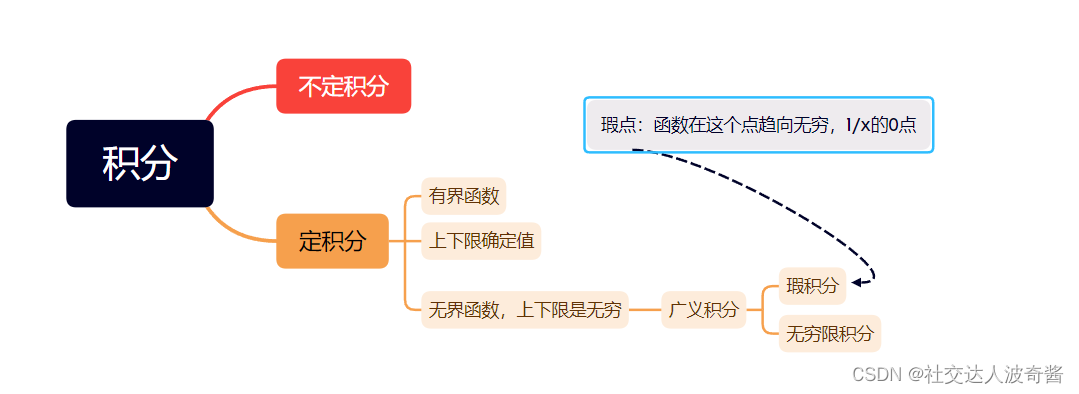
以y=1/(x^2)为例，本章节就是当上/下限无穷时（红色区域）或有瑕点时（绿色区域，0为瑕点）求函数围成的面积。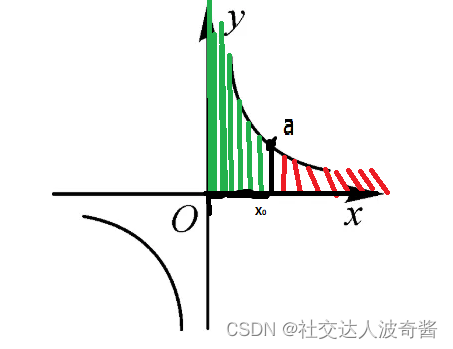 
证明广义积分收敛的方法
收敛和扩散概念的引入
将无穷限广义积分或瑕积分（被积函数连续）转变为积分上限/下限函数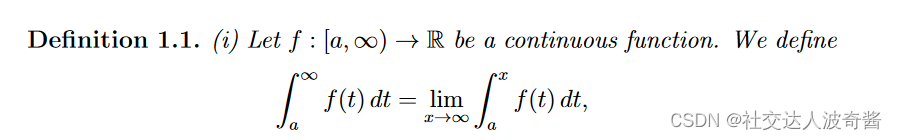 
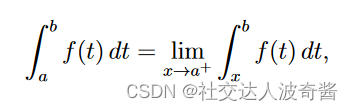
（假设b为瑕点） 假如极限存在，称反常积分收敛。 若极限不存在，称反常积分扩散。 求原函数极限法 如上所示，直接求被积函数的原函数，再根据牛顿莱布尼茨公式求极限。 比较审敛法：用函数值的大小判断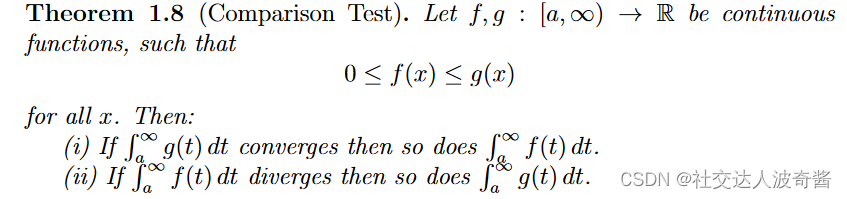
（如果是瑕积分，只需把上下限改变即可。） 注意f(x)和g(x)大于0 大函数收敛，小函数就收敛。 小函数扩散，大函就数扩散。 柯西判别法：把函数和1/x^p比较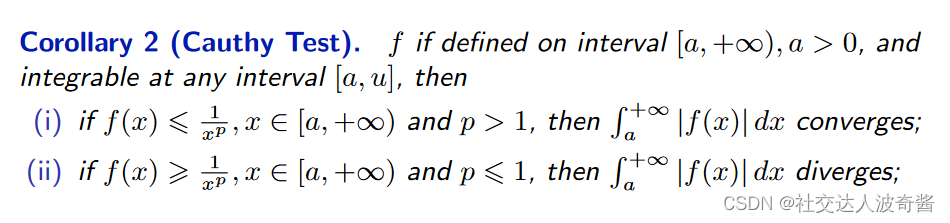
1/(x^p)函数的特殊性质
在[a,∞]（a>0）
p>1：反常积分是收敛的。
p∞换成x->a+)
(i)c在0到∞，两者反常积分收敛。 (ii)c=0，f（x）的量级低于g(x)。如果g(x)的反常积分收敛，那么f（x）的反常积分也收敛。 （iii）c=∞，f（x）的量级高于g（x）。如果g(x)的反常积分扩散，那么f(x)的反常积分也收散。 柯西测试的极限形式:把1换成入，x^p乘过去。
瑕积分就把x->∞变为x->a。 x^p变成（x-a）^p，注意p的取值对应情况刚好和无穷积分相反 
无穷积分 p>1,入>=0且不等于正无穷，反常函数收敛。 p0可以等于正无穷，反常函数扩散。 入为一个常数：此时1/x^p和函数同一个量级，对p范围的判断就可以判断出函数是否收敛。 入为0：说明函数是收敛函数，收敛函数的无穷限反常积分必然收敛。 入为无穷：此时1/x^p的量级小于函数。 关键就是构造出x^p使得结果为常数或为0。 阿贝尔判断：判断函数相乘结果是否收敛。
一个收敛，一个单调有界，瑕积分和无穷限积分区别在于区间范围不同。 分段证明收敛性上下限无穷/上限为无穷，下限为瑕点/但被被积函数的区间存在瑕点时，分开证明收敛性。 两侧无穷限广义积分收敛的条件：证明任一一侧无穷限广义积分都收敛。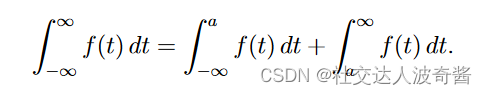 
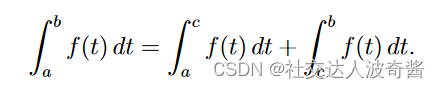
错误例子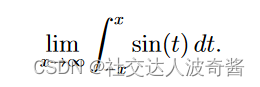 
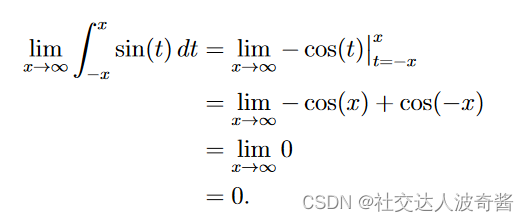
不能说明无极限广义积分收敛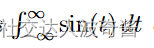 
其中a的选择不影响结果，证明过程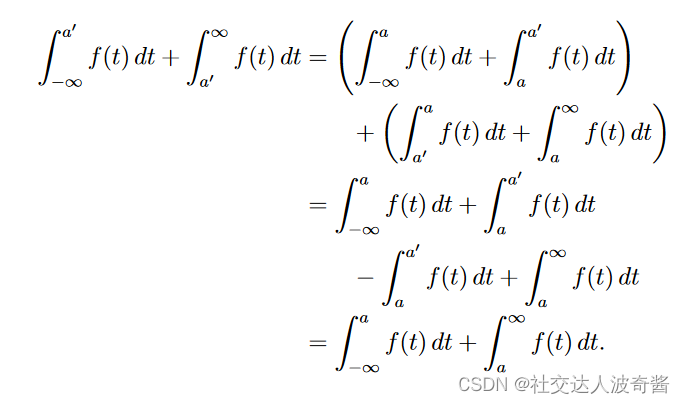 
判断上侧趋于无穷的定积分收敛与否小技巧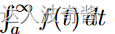 
绝对值和收敛性
f(x)的反常积分 |
【本文地址】
公司简介
联系我们