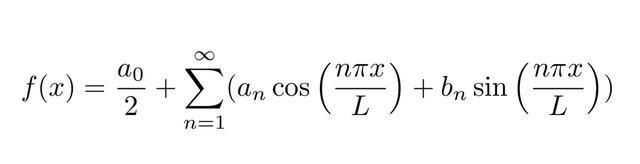数学史上创造的最强大的工具：傅里叶级数

关于d'Alembert和Euler的研究，我们不能不说，如果他们知道这种扩展，他们就可以很好地利用它。他们都相信，一个任意的、不连续的函数永远不可能用这种级数来求解，而且似乎甚至没有人在多弧的余弦中形成常数，这是我在热理论中要解决的第一个问题。--J。傅里叶

约瑟夫·傅里叶开始分析热方程时，一切就开始了，

这个方程就是所谓的线性偏微分方程，它的意思是，

如果我们有两个不同的解（Φ1和Φ2）并且满足边界条件，则可以这样写：

一个新的解= Y =（a×Φ1）+（b×Φ2）

其中a和b是2个任意常数，具体取决于初始条件。但是它是如此强大。如我们所知，该解决方案将使我们得到正弦和余弦函数的某种组合。所以呢？

为了理解我的意思，我们举一个简单的例子。我们将考虑一个假想的完美金属棒，该棒的中点在两个不同的侧面上有2个不同的温度。让我们以图形方式了解我的意思：

如果我们把温度标在y轴上，把位置标在x轴上，你可以看到，我们就得到了所谓的阶跃函数。

但是，请稍等，我告诉您，我们从热方程式中获得的解决方案是余弦或正弦函数的线性组合。

但是我们假定的杆系统也可以用相同的方法求解，并且应该给我们正弦和余弦的线性组合（我们将使用周期正余弦函数得到阶跃函数）

这就是傅里叶迈出的一步，在科学界变得不朽

正如你在视频中看到的，随着我们不断添加余弦或正弦或它们的组合(取决于边界条件)和适当的系数(在我们的讨论中类似于a和b)，我们得到的结果接近我们想要的函数。但是我们的函数是不连续的，即使这样也不能阻止我们!!，现在你明白它有多强大了吧?你可能会说，它看起来像我们的函数，但并不完全是那样，我会说，是的，你是对的。我们得到的只是一个近似值但随着我们加入上面所示的微分方程的越来越多的解，我们会越来越接近我们的函数。这尝试增加数量的项，看看你如何接近那个函数(更一般的方波)。

现在我们明白了这个美妙方法背后的含义。现在我们来看看如何计算1。

函数的傅里叶级数：

如果某个实变量x的函数f（x）在区间（c，c+2L）中定义并可积，满足Dirichlet条件，即：。，

f（x）是单值且有限，

f（x）是分段连续的，最多有有限个不连续点，

f（x）在区间内至多有有限个极大值和极小值，

然后f（x）可以在这个区间展开成下列级数，称为Fourier级数

注意，我没有写f（x）是周期的，因为我们可以把f（x）写成一个级数，即使函数不是周期性的。

如果我们考虑时间的函数，周期为T，即在区间（c，c+T），那么我们可以写出

式中ω=2π/T，T=2L。

在这两个方程a0中，an和bn称为Fourier常数，由

(a0/2)的值是通过n = 0得到的，所以我没有写出来。

有关用傅里叶级数表示一个函数的可能性的问题是麻烦的。幸运的是，几乎所有与物理问题有关的函数都被狄利克雷条件所覆盖。傅里叶定理是证明傅里叶级数收敛于与给定函数密切相关的函数的一组充分条件。

我们已经知道，我们可以将任意函数(满足一定条件)展开成一系列的正弦和余弦。但要理解这个，我们必须回到这个方程

e^（iθ）= cos（θ）+ i sin（θ）;其中i是-1的平方根

这个方程告诉我们，e^（iθ）表示一个圆，cos（θ）和sin（θ）也一样。使用这个简单但强大的标识，我们可以根据指数函数来写f（x），并在2D平面中用圆圈表示它们。

就像你在这段视频中看到的，我们画了一条从它的顶端到虚轴的垂直线。因为它而产生的曲线是我们古老的正弦曲线。

类似地，如果我们画一条从尖端到实轴的垂线，我们可以得到一条余弦曲线。

因此，使用上恒等式，我们可以将f（x）写成：

现在你可以看到这些圆圈是从哪里来的。在这个系列中，每个指数项实际上代表一个具有一定频率(由括号内的项给出)和一定半径(由cn给出)的旋转圆。这些圆结合在一起就得到了你们之前看到的曲线或函数。

这里cn等于(an-ibn)/2, c-n等于(an+ibn)/2。这些常数是，

级数的收敛:

如果f(x)和f ' (x)在-L到L上分段连续，且f(x)满足狄利克雷条件，则根据傅里叶定理可得:

f(x)的傅里叶级数收敛于(f(x+)+f(x-))/2

如果f (x) =不连续点x0,那么f (x)的傅里叶级数收敛于(f (x0 +)+ f (x0-))/ 2→0。

奇偶函数的技巧:

当我们展开任何函数时我们会得到一个方程左边等于以右边。因为两边必须相等，如果一条边是偶函数，那么另一条也必须是偶函数，如果一条是奇数，那么另一条也必须是奇数。这个简单的想法是非常深远的，它降低了计算的复杂性。

我们知道余弦是偶函数如果f(x)=f(-x)那么f(x)的展开式只包含余弦项，如果f(x)=-f(-x)那么f(x)的展开式只包含sin项因为sin是奇函数。

计算:

以方波的傅里叶级数为例:

你可以看到方波的定义如下所示。

你可以注意到f(t)=-f(-t)这意味着只有当我们展开这个函数时，我们必须有奇数项。这意味着我们只有sin项，也就是。，系数为bn的项。这个发现减少了一半的工作量我们现在只考虑sin项而不是cos项。

要解决这个问题，就像我之前说的，我们只需要bn，

结束:

傅里叶级数是表示某些函数的一种方法(大部分是周期函数)。从经典物理学到量子力学，甚至在数据处理中，它都被使用。它是数学有史以来创造的最强大的工具之一。

我们已经讨论了这么多，但到现在还剩下很多话题。这篇文章已经很长了，所以我们将在以后讨论剩下的事情。我希望这篇文章能帮助你建立直觉，并帮助你解决许多基本问题。我们的讨论到此结束