| 傅里叶变化、加窗傅里叶变化、短时傅里叶变化和小波变化 · 大专栏 | 您所在的位置:网站首页 › 傅里叶变换时为什么要加窗 › 傅里叶变化、加窗傅里叶变化、短时傅里叶变化和小波变化 · 大专栏 |
傅里叶变化、加窗傅里叶变化、短时傅里叶变化和小波变化 · 大专栏
|
最近正在写一篇关于小波神经网络的论文,找了一些资料查阅。在翻阅资料时发现它和之前学过的傅里叶变化有着很深的渊源,所以结合看的几篇博客以及一些文献,把这些基础的东西记录下来以免淡忘。先做个小总结:傅里叶变换:知道一段时间内,信号的各个频率分量有分别多少。小波变换:知道一段时间内,信号的各个频率分量有分别多少,以及他们都是什么时候出现的。参考文章:https://www.zhihu.com/question/22864189/answer/40772083 https://blog.csdn.net/weixin_38084653/article/details/78022264 1、变换在展开叙述之前,我们首先要理解两个问题:在大多数数字处理应用中,什么是变换?为什么我们需要变换? 实践应用中的大部分信号都是原始格式的时域信号。也就是说,无论这个信号是测量什么的,它都是一个关于时间的函数。换句话说,当我们绘制信号时,其中一个轴为时间(自变量),另外一个轴通常为振幅(因变量)。因此,当绘制时域信号时,需要获得信号的时间 - 振幅关系表示。但对于大多数信号处理应用来说,这些表示并不总是信号的最佳表示。大大多数情况下,信号的频率中包含着最重要的信息。基本上,信号的频谱就是信号的频率组成。信号的频谱可以显示出信号中存在怎样的频率。 我们了解,频率和变化率相关。如果一个事物急速变化,我们就说它具有高频特征;反之,如果一个变量没有急速变化(例如,它的变化很缓慢),我们就说它具有低频特征;如果一个变量不会发生任何改变,则其频率为 0。例如,日报的出版频率高于月刊。 频率以周期/秒 (cycles/second) 或者赫兹 (Hz) 为单位测量。例如,美国的日常电流频率为 60Hz。那么,你在绘制电流图时,你会得到一个周期为 1/50s 的正弦图。下图分别给出了 3Hz、10Hz、50Hz 的正弦波。 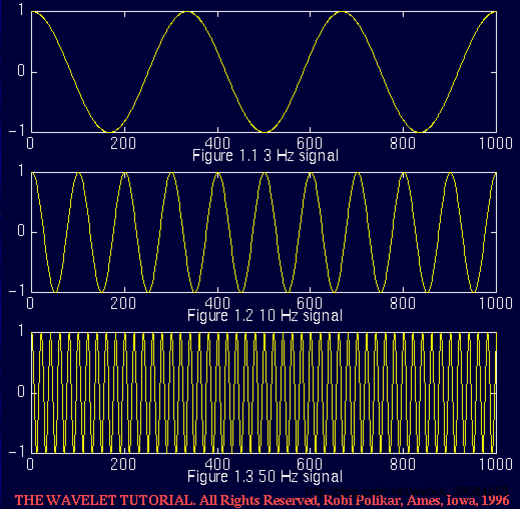
因此,如何测量频率?如何发现信号中的频谱?答案是——傅里叶变换(FT)。如果对一个时域信号进行了傅里叶变换,那么就可以获得这个信号的频率 - 振幅表示。换句话说,就可以得到包含 频率轴和振幅轴 的坐标系。(虽然傅里叶变换是应用最广的变换方式(特别是在电气工程中),但是,它并不是唯一一种变换方式。还有很多其他的变换方式: Hilbert transform、short-time Fourier transform (more about this later)、Wigner distributions、the Radon Transform、our featured transformation、the wavelet transform。每一种变换方式都有其自身的应用领域,以及优缺点,) 代表频率的轴的值从零开始延伸到无穷大。每一个频率值对应一个振幅值。例如,如果对家用电流进行傅里叶变换,将只会在 50Hz 处得到一个峰,因为电流信号只有一个 50Hz 的频率成分。实际情况中,信号通常会包含一个以上频率成分。下图给出了信号频率为 50Hz 的傅里叶变换。 
值得注意的是,上图给出了两个小图,底部图是顶部图的一半。基于现在还不必知道的原因,实值信号的频谱总是对称的。顶部图展示了这一点。然而,因为对称部分是初始部分的镜像,所以,对称部分并没有提供更多的信息,因此,通常情况下,不会将对称部分展示出来。 2、傅里叶变换(FT)傅立叶变换有助于理解常见的信号,以及如何辨别信号中的错误。 尽管傅立叶变换是一个复杂的数学函数,但是通过一个测量信号来理解傅立叶变换的概念并不复杂。 从根本上说,傅立叶变换将一个信号分解为不同幅值和频率的正弦波。 我们通常把一个实际信号看作是根据时间变化的电压值。 这是从时域的角度来观察信号。 傅立叶定律指出,任意波形在时域中都可以由若干个正弦波和余弦波的加权和来表示。 例如,有两个正弦波,其中一个的频率是另一个的 3 倍。将两个正弦波相加,就得到了一个不同的信号。 
通过这种方法,所有时域中的信号都可表示为一组正弦波。即使可以通过这种方法构造信号,那意味着什么呢?因为可以通过正弦波构造信号,同理也可以将信号分解为正弦波。 一旦信号被分解,可查看和分析原信号中不同频率的信号。但是对于傅里叶变换而言,也存在一定的局限性。傅里叶变换给出了信号的频率信息,也就意味着它可以告诉我们该信号中各种频率的个数,但是不能告诉我们特定频率在何时存在。当信号是平稳状态时,这一信息是不需要的。对非平稳过程,傅里叶变换有局限性以下面这一信号为例: x(t)=cos(2∗pi∗10∗t)+cos(2∗pi∗25∗t)+cos(2∗pi∗0∗t)+cos(2∗pi∗100∗t)这是一个平稳信号,因为不论何时它都具有 10,25,50 和 100Hz 的频率。这个信号可以绘制成如下图: 
做完 FFT 后,可以很清楚的看到信号包含四个频率成分,但是如果频率是随着时间变化的非平稳信号呢? 
如上图,最上边的是频率始终不变的平稳信号。而下边两个则是频率随着时间改变的非平稳信号,它们同样包含和最上信号相同频率的四个成分。做 FFT 后,我们发现这三个时域上有巨大差异的信号,频谱却非常一致。尤其是下边两个非平稳信号,我们从频域上无法区分它们,因为它们包含的四个频率的信号的成分确实是一样的,只是出现的先后顺序不同。 可见,傅里叶变换处理非平稳信号有天生缺陷。它只能获取一段信号总体上包含哪些频率的成分,但是对各成分出现的时刻并无所知。因此时域相差很大的两个信号,可能频谱图一样。 然而平稳信号大多是人为制造出来的,自然界的大量信号几乎都是非平稳的,所以在比如生物医学信号分析等领域中,基本看不到单纯傅里叶变换这样的方法。 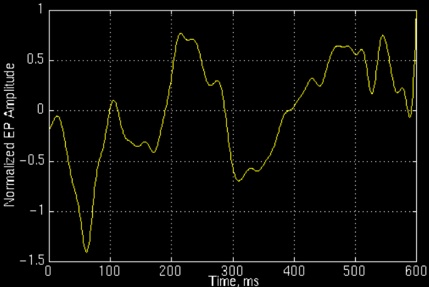
上图所示的是一个正常人的事件相关电位。对于这样的非平稳信号,只知道包含哪些频率成分是不够的,我们还想知道上图所示的是一个正常人的事件相关电位。对于这样的非平稳信号,只知道包含哪些频率成分是不够的,我们还想知道各个成分出现的时间。知道信号频率随时间变化的情况,各个时刻的瞬时频率及其幅值——这也就是时频分析。 二、短时傅里叶变换(STFT)一个简单可行的方法就是——加窗。把整个时域过程分解成无数个等长的小过程,每个小过程近似平稳,再傅里叶变换,就知道在哪个时间点上出现了什么频率了。这就是短时傅里叶变换。 
时域上分成一段一段做 FFT,不就知道频率成分随着时间的变化情况了吗!时域上分成一段一段做 FFT,不就知道频率成分随着时间的变化情况了吗!用这样的方法,可以得到一个信号的时频图了: 
图上既能看到 300Hz,200Hz,100Hz,50Hz 四个频域成分,还能看到出现的时间。两排峰是对称的,所以大家只用看一排就行了。使用 STFT 存在一个问题,我们应该用多宽的窗函数?窗太宽太窄都有问题: 

窗太窄,窗内的信号太短,会导致频率分析不够精准,频率分辨率差。窗太宽,时域上又不够精细,时间分辨率低。窗太窄,窗内的信号太短,会导致频率分析不够精准,频率分辨率差。窗太宽,时域上又不够精细,时间分辨率低。看看实例效果吧: 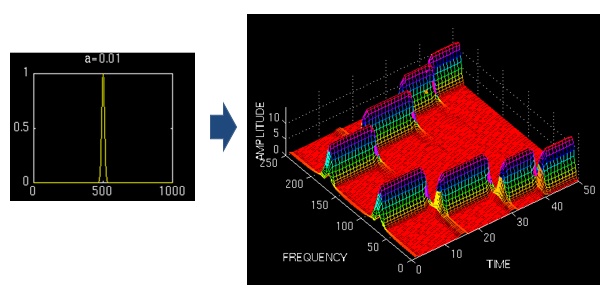


上图对同一个信号(4 个频率成分)采用不同宽度的窗做 STFT,结果如右图。用窄窗,时频图在时间轴上分辨率很高,几个峰基本成矩形,而用宽窗则变成了绵延的矮山。但是频率轴上,窄窗明显不如下边两个宽窗精确。所以窄窗口时间分辨率高、频率分辨率低,宽窗口时间分辨率低、频率分辨率高。对于时变的非稳态信号,高频适合小窗口,低频适合大窗口。然而 STFT 的窗口是固定的,在一次 STFT 中宽度不会变化,所以 STFT 还是无法满足非稳态信号变化的频率的需求。 三、小波变换那么你可能会想到,让窗口大小变起来,多做几次 STFT 不就可以了吗?!没错,小波变换就有着这样的思路。 但事实上小波并不是这么做的,小波变换并没有采用窗的思想,更没有做傅里叶变换。至于为什么不采用可变窗的 STFT 呢,我认为是因为这样做冗余会太严重,STFT 做不到正交化,这也是它的一大缺陷。于是小波变换的出发点和 STFT 还是不同的。STFT 是给信号加窗,分段做 FFT;而小波直接把傅里叶变换的基给换了——将无限长的三角函数基换成了有限长的会衰减的小波基。这样不仅能够获取频率,还可以定位到时间了。 (注释:什么是正交化?为什么说小波能实现正交化是优势?简单说,如果采用正交基,变换域系数会没有冗余信息,等于是用最少的数据表达最大的信息量,利于数值压缩等领域。JPEG2000 压缩就是用正交小波变换。比如典型的正交基:二维笛卡尔坐标系的(1,0)、(0,1),用它们表达一个信号显然非常高效,计算简单。而如果用三个互成 120°的向量表达,则会有信息冗余,有重复表达。但是并不意味着正交一定优于不正交。比如如果是做图像增强,有时候反而希望能有一些冗余信息,更利于对噪声的抑制和对某些特征的增强。)【解释】来我们再回顾一下傅里叶变换吧,没弄清傅里叶变换为什么能得到信号各个频率成分的同学也可以再借我的图理解一下。傅里叶变换把无限长的三角函数作为基函数: 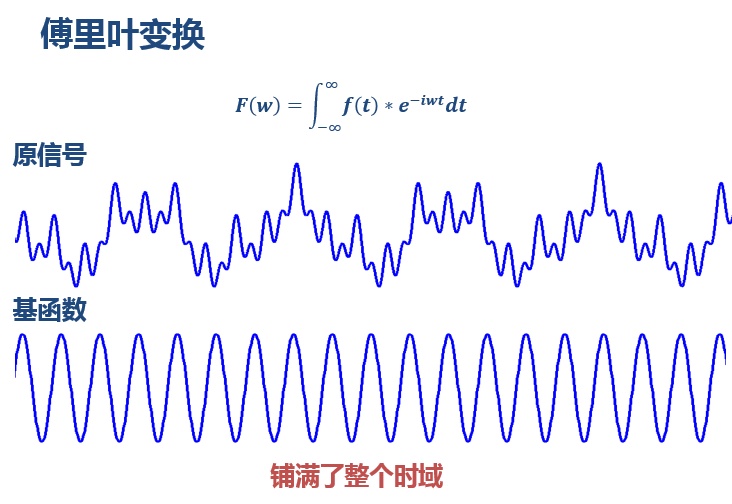
这个基函数会伸缩、会平移(其实是两个正交基的分解)。缩得窄,对应高频;伸得宽,对应低频。然后这个基函数不断和信号做相乘。某一个尺度(宽窄)下乘出来的结果,就可以理解成信号所包含的当前尺度对应频率成分有多少。于是,基函数会在某些尺度下,与信号相乘得到一个很大的值,因为此时二者有一种重合关系。那么我们就知道信号包含多少该频率的成分。那么我们就知道信号包含改频率的成分的多少。仔细体会可以发现,这一步其实是在计算信号和三角函数的相关性。 
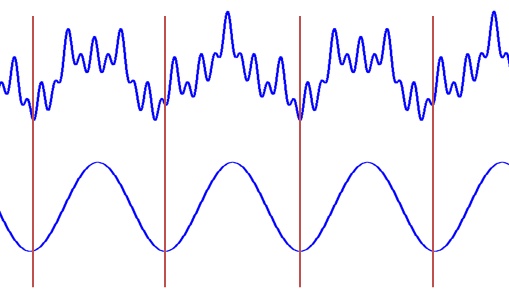
看,这两种尺度能乘出一个大的值,所以信号包含较多的这两个频率成分,在频谱上这两个频率会出现两个峰。以上,就是粗浅意义上傅里叶变换的原理。 如前面所说,小波做的改变就在于,将无限长的三角函数基换成了有限的会衰减的小波基。 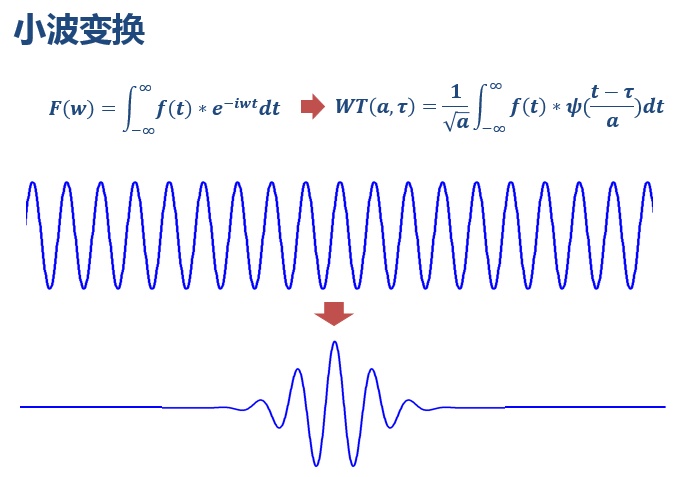
为什么叫 “小波”,因为是很小的一个波: 
从公式可以看出,不同于傅里叶变换,变量只有频率ω,小波变换有两个变量:尺度 a(scale)和平移量 τ(translation)。尺度 a 控制小波函数的伸缩,平移量τ控制小波函数的平移。尺度就对应于频率(反比),平移量 τ就对应于时间。 
当伸缩、平移到这么一种重合情况时,也会相乘得到一个大的值。这时候和傅里叶变换不同的是,这不仅可以知道信号有这样频率的成分,而且知道它在时域上存在的具体位置。而当我们在每个尺度下都平移着和信号乘过一遍后,我们就知道信号在每个位置都包含哪些频率成分。做傅里叶变换只能得到一个频谱,做小波变换却可以得到一个时频谱!对于同一个时域信号而言,下图可以显著看出两者的区别: 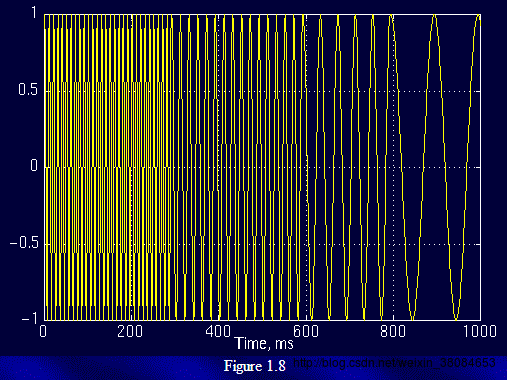 图一:时域信号 图一:时域信号
 图二:傅里叶变换后的结果 图二:傅里叶变换后的结果
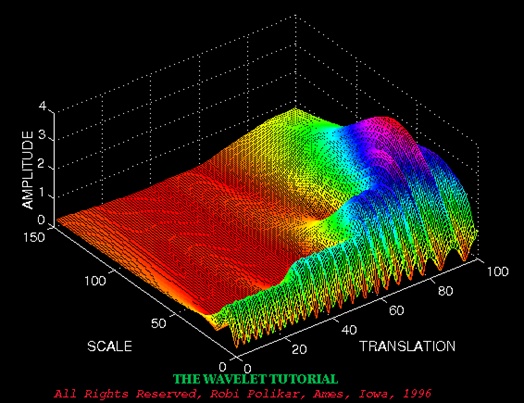 图三:小波变换后的结果 图三:小波变换后的结果
小波还有一些好处:1、我们知道对于突变信号,傅里叶变换存在吉布斯效应,我们用无限长的三角函数怎么也拟合不好突变信号: 
然而衰减的小波就不一样了: 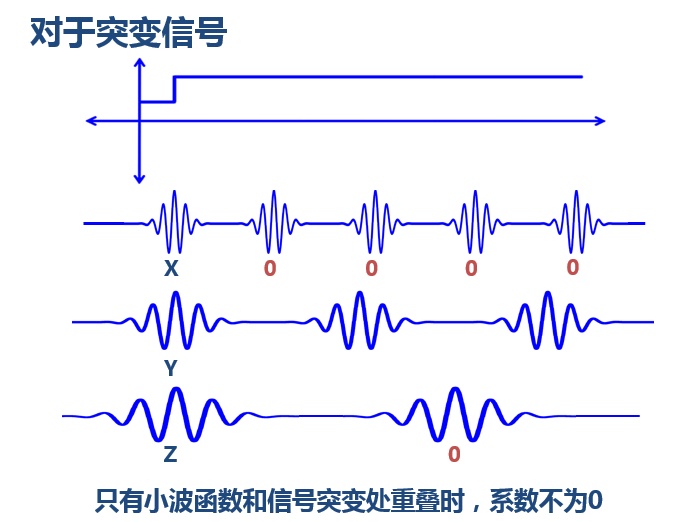
以上,就是小波的意义。利用文章开头总结的两句话粗略的概况一下:傅里叶变换:知道一段时间内,信号的各个频率分量有分别多少。小波变换:知道一段时间内,信号的各个频率分量有分别多少,以及他们都是什么时候出现的。 |
【本文地址】