从零学习Belief Propagation算法（一）

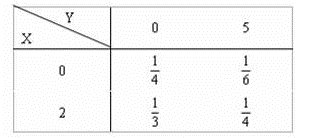
本文将记录 Belief Propagation 算法的学习历程，如果您之前没有接触过，而现在刚好需要用到，可以参考我的系列文章。内容稍多将分为几个主题来写。本系列文章将包含以下内容：

我们要学习的算法称作 Belief Propagation，简称 BP 算法。

我们可以叫它置信度传播算法，也可以称作信念传播算法；它的原始名称是 算法（Sum-Product Algorithm），又称 概率传播（Probability Propagation )算法；为了统一起见，我们下面都会用 BP 表示该算法。

BP 算法涉及到了概率图模型（Graphical Model），即涉及到了概率论和图论，当然不是全部的知识都需要学习，我们只需要了解其中一部分我们需要的就可以。

需要注意的是，Belief Propagation 并不是神经网络中的 Back Propagation（反向传播算法），不过却有着一定得联系。 另外不得不吐槽一下，网上关于反向传播的算法资料太多了（因为深度学习/神经网络的原因吧），关于信念传播的算法资料有限，讲解的好的更是少之又少。特此感谢那几篇仅有的资料让我整合一下。

接下来所有考虑都是以离散型随机变量为例！连续型随机变量也是同理。

(1) P ( X ∣ Y ) = P ( X , Y ) P ( Y ) P(X|Y) = \frac{P(X, Y)}{P(Y)}\tag1 P(X∣Y)=P(Y)P(X,Y)​(1) 若 X 、 Y X、Y X、Y相互独立： P ( X ∣ Y ) = P ( X , Y ) P ( Y ) = P ( X ) P ( Y ) P ( Y ) = P ( X ) P(X|Y) = \frac{P(X, Y)}{P(Y)}=\frac{P(X) P(Y)}{P(Y)}=P(X) P(X∣Y)=P(Y)P(X,Y)​=P(Y)P(X)P(Y)​=P(X)

(2) P ( X ∣ Y ) = P ( Y ∣ X ) P ( X ) P ( Y ) P(X|Y) = \frac{P(Y|X)P(X)}{P(Y)}\tag2 P(X∣Y)=P(Y)P(Y∣X)P(X)​(2) 先 验 分 布 + 样 本 信 息 → 后 验 分 布 先验分布 + 样本信息 → 后验分布 先验分布+样本信息→后验分布 关于贝叶斯的公式如何理解，我的前几期博客总结好了，如果您觉得这个公式仅仅是会应付做题但没有真正理解，请看 这里。

贝叶斯的一个应用：

当你在Google中输入“laern”时，系统会猜测你的意图：是不是要搜索“learn”。Google的拼写检查基于贝叶斯方法。下面解析怎么利用贝叶斯方法实现"拼写检查"的功能。 用户输入一个词时：可能拼写正确，也可能拼写错误。如果把拼写正确记做 c c c（代表correct），拼写错误记做 w w w（代表wrong）。那么"拼写检查"要做的事情就是：在发生 w w w的情况下，试图推断出 c c c。即：已知 w w w，然后在若干个可能的备选方案中，找出可能性最大的那个 c c c。 a r g m a x c P ( c ∣ w ) = a r g m a x c P ( w ∣ c ) ∗ P ( c ) P ( w ) \underset{c}{argmax} P(c|w)=\underset{c}{argmax} \frac{P(w|c) *P(c)}{P(w)} cargmax​P(c∣w)=cargmax​P(w)P(w∣c)∗P(c)​ 由于对于所有备选的 c c c来说，对应的都是同一个 w w w，所以它们的 P ( w ) P(w) P(w)是相同的，因此我们只要最大化 $ P(w|c) *P©$，即： a r g m a x c P ( c ∣ w ) = a r g m a x c P ( w ∣ c ) ∗ P ( c ) \underset{c}{argmax} P(c|w)=\underset{c}{argmax} {P(w|c) *P(c)} cargmax​P(c∣w)=cargmax​P(w∣c)∗P(c)

(3) P ( X = x i , Y = y i ) = p i j ； （ i , j = 1 , 2 , … . ） P(X=x_i, Y=y_i) = p_{ij}；（i,j=1,2,….）\tag3 P(X=xi​,Y=yi​)=pij​；（i,j=1,2,….）(3)

例如： X X X 的状态有2个：{0，2}； Y Y Y 的状态有2个：{0，5}； X 、 Y X、Y X、Y联合起来的状态就是一个 2 ∗ 2 2*2 2∗2的表格。 P ( X = 0 , Y = 5 ) = 1 6 P(X=0, Y=5) = \frac{1}{6} P(X=0,Y=5)=61​ ∑ i ， j P ( X = x i , Y = y i ) = 1 4 + 1 6 + 1 3 + 1 4 = 1 \sum_{i，j}P(X=x_i, Y=y_i) =\frac{1}{4}+\frac{1}{6}+\frac{1}{3}+\frac{1}{4}= 1 i，j∑​P(X=xi​,Y=yi​)=41​+61​+31​+41​=1 联合概率也是可以这么求的（通过条件概率的乘积）： (4) P ( X 1 , X 2 , X 3 ) = P ( X 1 ) P ( X 2 ∣ X 1 ) P ( X 3 ∣ X 1 , X 2 ) P(X_1,X_2,X_3) =P(X_1) P(X_2|X_1)P(X_3|X_1,X_2)\tag4 P(X1​,X2​,X3​)=P(X1​)P(X2​∣X1​)P(X3​∣X1​,X2​)(4)

(5) P ( X = x i ) = ∑ j p i j ； （ i = 1 , 2 , 3 … . . n ） P(X = x_i) =\sum_{j} p_{ij} ；（ i=1,2,3…..n）\tag5 P(X=xi​)=j∑​pij​；（i=1,2,3…..n）(5)

例如： X X X 的状态有2个：{0，2}； Y Y Y 的状态有2个：{0，5}；下面以 X X X为例。求 X X X的边缘分布， X X X可取两种状态，方法就是在每种状态下 消除 Y Y Y。

P ( X = 2 ) = ∑ Y P ( X = 2 ， Y ) = P ( X = 2 ， Y = 0 ) + P ( X = 2 ， Y = 5 ) P(X=2) \\= \sum_{Y}P(X=2，Y)\\=P(X=2，Y=0)+P(X=2，Y=5) P(X=2)=∑Y​P(X=2，Y)=P(X=2，Y=0)+P(X=2，Y=5) ∴ P ( X = 2 ) = 1 3 + 1 4 = 7 12 ∴ P(X=2)=\frac{1}{3}+\frac{1}{4}=\frac{7}{12} ∴P(X=2)=31​+41​=127​ 第二种状态： ∴ P ( X = 0 ) = 1 4 + 1 6 = 5 12 ∴ P(X=0)=\frac{1}{4}+\frac{1}{6}=\frac{5}{12} ∴P(X=0)=41​+61​=125​

可见，求边缘分布的方法是消除其余的变量，如何消除呢？如上例子，求 X X X 的边缘分布就要对联合分布在 Y Y Y 上 加和（离散）或者积分（连续）。

为什么我们在这里用这么大篇幅叙述边缘分布呢，因为后面的 BP 算法运算就是从这里下手的。 对于很多个随机变量比如 U 、 V 、 W 、 X 、 Y 、 Z U、V、W、X、Y、Z U、V、W、X、Y、Z，求 X X X的边缘分布的公式如下：

P ( X ) = ∑ U ∑ V ∑ W ∑ Y ∑ Z P ( U , V , W , X , Y , Z ) = ∑ U , V , W , Y , Z P ( U , V , W , X , Y , Z ) P(X) =\sum_{U}\sum_{V}\sum_{W}\sum_{Y}\sum_{Z} P(U,V,W,X,Y,Z) \\=\sum_{U,V,W,Y,Z}P(U,V,W,X,Y,Z) P(X)=U∑​V∑​W∑​Y∑​Z∑​P(U,V,W,X,Y,Z)=U,V,W,Y,Z∑​P(U,V,W,X,Y,Z)

若两个节点间以一个单箭头连接在一起，表示其中一个节点是“因(parents)”，另一个是“果(children)”，两节点就会产生一个条件概率值。

下图中 E 是因（父节点），H 是果（子节点）。

典型的概率图模型包括贝叶斯网络和马尔科夫随机场（MRF）。 贝叶斯网络是有向图模型，用于表示随机变量之间的因果关系；而马尔科夫随机场是无向图模型，用于表示随机变量的概率分布推理或者说是随机变量之间的软约束关系；最后可以由前两种网络构造新的结构叫做因子图（factor graph）。

[1] : http://blog.csdn.net/aspirinvagrant/article/details/40862237 [2] : http://blog.csdn.net/v_july_v/article/details/40984699 [3] : http://blog.csdn.net/qq_23947237/article/details/78319547