| 梯度下降法(GD)与随机梯度下降法(SGD)的理解 | 您所在的位置:网站首页 › 什么是梯度下降法的概念 › 梯度下降法(GD)与随机梯度下降法(SGD)的理解 |
梯度下降法(GD)与随机梯度下降法(SGD)的理解
|
引言: 在深度学习的任务目标中,通常我们希望我们的学习结果能够在损失函数上得到一个较好的结果,即朝着损失函数最小的方向前进。接下来我会用比较通俗易懂的语言来介绍GD、SGD 下一篇:通俗易懂理解(梯度下降)优化算法:Momentum、AdaGrad、RMSProp、Adam 梯度下降法(gradient descent): 1. 数学理解 首先我们知道梯度方向是函数增长最快的方向,梯度的反方向是函数减少最快的方向,而梯度下降法就是往梯度反方向前进"一小步"来达到函数减少的效果。对于二维空间,其下降的方式大致为下图(这里我默认大家都理解等高线):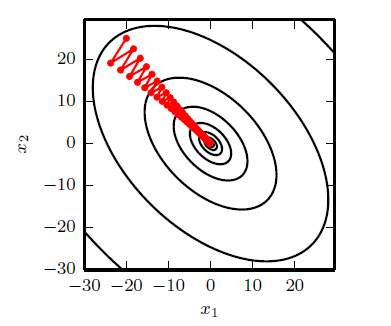 接下来,我们来理解为什么是"一小步",而不是"一大步"? 首先,我们知道,我们一般执行梯度下降是采用下面这个形式:
接下来,我们来理解为什么是"一小步",而不是"一大步"? 首先,我们知道,我们一般执行梯度下降是采用下面这个形式:
x = x − η ∇ g x=x-\eta\nabla g x=x−η∇g 其中 η \eta η就是我们的学习率, g g g是梯度。 我们可以从一元函数的 t a y l o r taylor taylor公式展开的角度来理解这个问题: f ( x + η ) ≈ f ( x ) + f ′ ( x ) η + O ( η 2 ) f(x+\eta)\approx f(x)+f' (x)\eta+O(\eta^2) f(x+η)≈f(x)+f′(x)η+O(η2) 其中 f ′ ( x ) = ∇ g f'(x)=\nabla g f′(x)=∇g。首先,可以从这个近似中(因为我们就只展开了两项,所以 η \eta η不能太大)得知 η \eta η足够小时才能近似成立,这也就回答了为什么我们要走"一小步",此外,如果我们把 η \eta η换成 − f ′ ( x ) η -f'(x)\eta −f′(x)η(此时 ( x − η f ′ ( x ) (x-\eta f'(x) (x−ηf′(x)就是我们常说的往负梯度方向进行更新一小步)然后有 f ( x − η f ′ ( x ) ) ≈ f ( x ) − [ f ′ ( x ) ] 2 η + O ( η 2 ) ⎵ ; = 0 f(x-\eta f'(x))\approx f(x)\underbrace{-[f'(x)]^2\eta+O(\eta^2)}_{;=0} f(x−ηf′(x))≈f(x)=0的原因 2. 梯度下降法确实能让我们目标函数减小 2. 图画理解 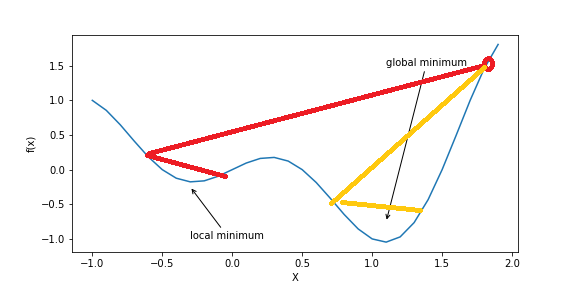 从图中我们可以看出,如果学习率较大,很有可能会陷入一个"局部最小值"而无法跳出
从图中我们可以看出,如果学习率较大,很有可能会陷入一个"局部最小值"而无法跳出
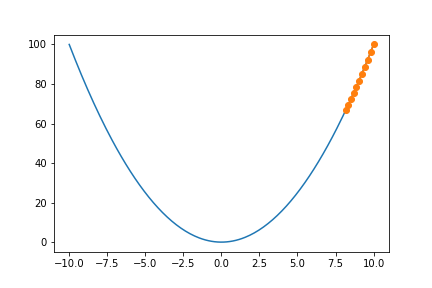 从图中我们可以看出,如果学习率较小,就需要很多迭代轮数
从图中我们可以看出,如果学习率较小,就需要很多迭代轮数
随机梯度下降法(Stochastic gradient descent): 随机梯度下降法(SGD)的思想就是按照数据生成分布抽取 m m m个样本,通过计算他们梯度的平均值来更新梯度(梯度下降法采用的是全部样本的梯度平均值来更新梯度)。 NOTE: 一般来说我们在实现SGD一般采用的都是以上方法,即通过每次取一个batch_size大小的样本来更新梯度而不是每次仅取1个样本来更新。 1. SGD与GD的比较: 在深度学习中,目标函数通常是训练数据集中各个样本的损失函数平均,即 f ( x ) = 1 n ∑ i = 1 n f i ( x ) f(x)= \frac{1}{n}\sum_{i=1}^{n}f_i(x) f(x)=n1i=1∑nfi(x)其中, f i ( x ) f_i(x) fi(x)是第i个样本所对应的损失函数, f ( x ) f(x) f(x)是目标损失函数。 通常,对于梯度下降法而言,其梯度的计算公式为 ∇ f ( x ) = 1 n ∑ i = 1 n ∇ f i ( x ) \nabla f(x)=\frac{1}{n}\sum_{i=1}^{n}\nabla f_i(x) ∇f(x)=n1i=1∑n∇fi(x)其计算复杂度为 O ( n ) O(n) O(n)而随机梯度下降法其梯度的计算公式为 ∇ f ( x ) = 1 m ∑ i = 1 m ∇ f i ( x ) \nabla f(x)=\frac{1}{m}\sum_{i=1}^{m}\nabla f_i(x) ∇f(x)=m1i=1∑m∇fi(x)其计算复杂度为 O ( 1 ) O(1) O(1),因为 m m m不会随着 n n n的增大而明显改变,这就可以大大减少我们的计算复杂度。 2. batch_size的选择: 一般来说,batch_size也就是 m m m一般选择为2的整数次幂。 学习率总结 对于学习率,一般来说我们有如下共识: 1. 较小的学习率意味着收敛速度慢,需要很多的迭代步数; 2.较大的学习率不仅会让前面的 t a y l o r taylor taylor公式近似不成立,此外也可能因为太大而导致陷入"比较差"的局部最小值 [1] Ian Goodfellow,Yoshua Bengio,Aaron courville.深度学习[M].人民邮电出版社. [2] 动手学习深度学习. 李沐 如果觉得我有地方讲的不好的或者有错误的欢迎给我留言,谢谢大家阅读(点个赞我可是会很开心的哦)~ |
【本文地址】