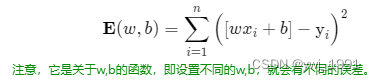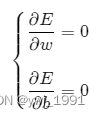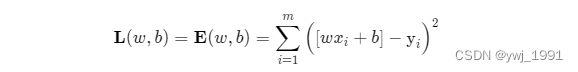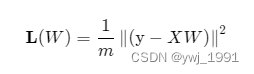| 从《线性回归》学习模型三要素 | 您所在的位置:网站首页 › 什么是数据模型的三要素 › 从《线性回归》学习模型三要素 |
从《线性回归》学习模型三要素
|
《老饼讲解机器学习》专注于机器学习的学习网站 目录 一、初识模型 二、模型三要素 1、模型 2、损失函数 3、模型求解 三、完整的线性模型 (一) 模型表达式 (二) 损失函数 (三) 矩阵形式 (四) 模型的求解 四、实例讲解 (一) 问题 (二)建模思路 (三) 代码 五、总结 (一) 线性模型的使用 (二) 模型三组件 本文介绍《线性回归》----入门必备的第一个模型! 一、初识模型机器学习的主要任务是就是进行预测。 (一) 模型思路 假如我们有一组数据,年龄与身高,我们希望通过年龄预测身高。
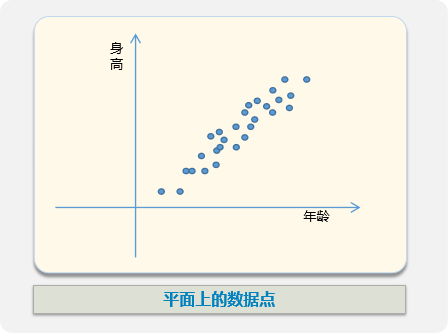
把x,y画在坐标轴上如下:
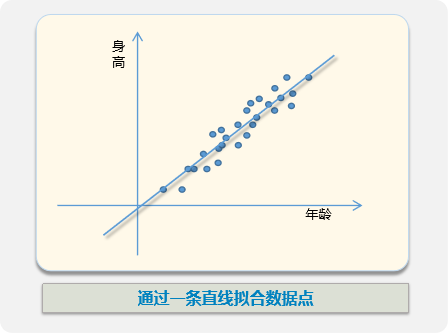
可以发现,身高和年龄是有强烈的线性关系的。 那么,我们可以假设它们的关系是y = wx +b 。 (二)模型目标 现在,我们需要确定一组[w,b],使y = wx+b得到的结果 与实际误差最小。
我们可以用所有预测样本的总平方误差作为我们误差的衡量指标。 即
(三)模型求解 通过求取令误差E时最小时的[w,b], 就能确定最适合我们用来拟合数据点的直线。 实际就是求w,b取何值时,能令E 最小的数学问题。 如下,令E的偏导数(即分别对w,b求导,多元函数称为偏导,用
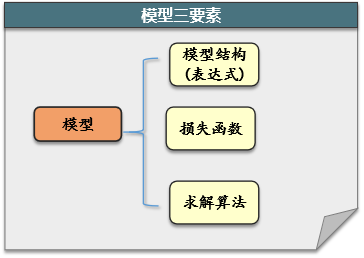
两个线性方程 ,两个未知数,联立求解即可得到w,b。 二、模型三要素通过上面的思路,我们引出了模型的三个重要组成部分。
模型确定了你要用什么样的结构去拟合数据点,在本例我们用的是直线
损失函数也叫代价函数,即这里的误差函数,说明我们采用某组w,b时,所要耗费的代价、损失,在本例我们的损失就是预测精度(误差)的损失。
模型中预留一些待定参数(这里是w和b),损失函数给我们指明了我们想要的参数是什么,而模型求解,则是根据损失函数,解出最符合我们要求的参数。 模型求解也叫模型训练,训练模型即对模型求解。在这里我们用的是联立各个参数的偏导方程进行求解。 三、完整的线性模型我们把模型推广到多变量。 (一) 模型表达式
预测值与真实值的平方差
为书写方例,我们写成矩阵形式:(1) 模型表达式:
注意:矩阵形式里对原始X增加了一列常数1,则W比原来的变量多了一个,其实也就是把 b揉进了W里。 (2) 损失函数
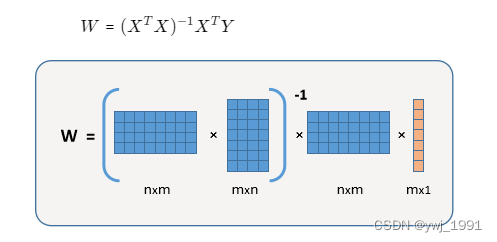
备注:这里的X是采集的样本数据(并加上一列常数1),是m*(n+1)的矩阵,每行代表一个样本 (四) 模型的求解我们不用真的去求偏导,直接使用公式即可,
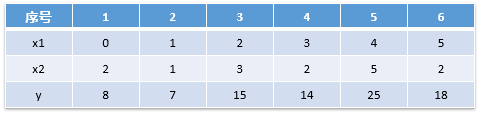
该公式可以由求导并整理后推导出来,也可以使用广义逆矩阵的概念得到。但这并不重要,以后会讲解,这里知道有个已经总结好的公式就可以了。 四、实例讲解 (一) 问题例如,我们现在有以下数据:
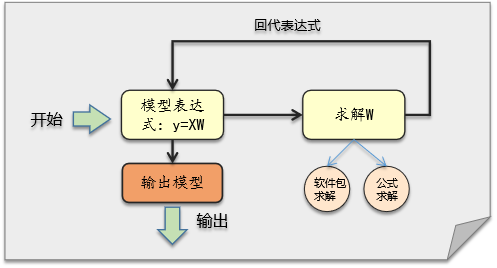
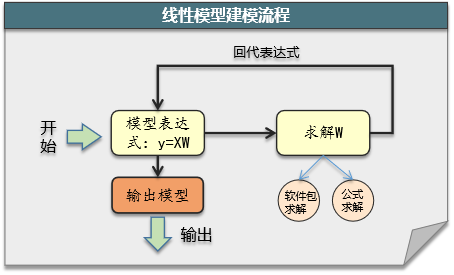
需要我们建立线性模型,用x1,x2变量,预测y。 ( 以上数据的实际关系为: 我们建模如下: (1) 假设变量服从 y =XW的关系。 (2) 求取最佳的W。 实际操作步骤很简单,只要把X添加一列1,然后用求解公式 求解W就可以了,就能得到我们的模型。
方法一:自写代码 自行编写代码如下: from sklearn import linear_model import numpy as np #输入数据 x = np.array([[0, 2], [1, 1], [2,3],[3,2],[4,5],[5,2]]) y = np.array([8,7,15,14,25,18]) # 给x添加一列1 xt = np.insert(x, x.shape[1], 1, axis=1) #按公式求解w,其中inv的功能是求矩阵的逆,@是矩阵的乘法 w = np.linalg.inv(xt.T@xt)@xt.T@y #输出W print("模型参数W:"+str(w))运行结果: 模型参数W:[2. 3. 2.]得到了W,代入模型,就得到我们的预测模型了: 方法二:用sklearn包 我们也可以用python机器学习包的sklearn的线性模型方法求解。 代码如下: from sklearn import linear_model import numpy as np #输入数据 x = np.array([[0, 2], [1, 1], [2,3],[3,2],[4,5],[5,2]]) y = np.array([8,7,15,14,25,18]) #调用sklearn的线性模型包,训练数据 reg = linear_model.LinearRegression() reg.fit(x,y) #输出系数和阈值 print("模型参数:"+str(reg.coef_)) print("模型阈值:"+str(reg.intercept_))运行结果: 模型参数:[2. 3.] 模型阈值:1.9999999999999982代入模型,即有: 本文我们学习了 (一) 线性模型的使用
(1) 先假设变量与y服从线性关系 y= XW (判断x与y是否成线性关系,依赖于我们对业务背景的了解,和变量的数据分析) (2) 按公式对W进行求解。 (3) 将求解的W代入模型。 (二) 模型三组件模型三组件:《模型》《损失函数》《模型求解》
1.《模型》 模型确定了我们模型的性质,例如,线性模型,它就是一条直线(或平面、超平面),如果我们x和y是条抛物线,那我们用线性模型就拟合不出来了。正因为如此,我们才需要不同的模型,对不同的业务,选择不同的模型。 2.《损失函数》 损失函数指定了我们的求解目标。 3.模型求解 从上面的例子我们就能感受到,模型求解其实就是整套代码的核心。随着模型越来越复杂,我们的求解过程、求解方法也会越来越复杂。 学习一个模型,往往模型公式一看,背景意义一理解,损失函数看一看,十分钟不到就到手了。但复杂的模型有更复杂的求解方法。学习模型最耗时间的是模型的求解。 相关文章 《入门篇-环境搭建:anaconda安装》 《入门篇-模型:逻辑回归》 《入门篇-模型:决策树-CART》 |
【本文地址】
| 今日新闻 |
| 推荐新闻 |
| 专题文章 |