| 【自动控制原理】以弹簧振动系统(典型二阶系统)为例理解系统微分方程与传递函数、控制框图的关系,闭环极点与稳定性的关系 | 您所在的位置:网站首页 › 二阶传感器动态响应参数 › 【自动控制原理】以弹簧振动系统(典型二阶系统)为例理解系统微分方程与传递函数、控制框图的关系,闭环极点与稳定性的关系 |
【自动控制原理】以弹簧振动系统(典型二阶系统)为例理解系统微分方程与传递函数、控制框图的关系,闭环极点与稳定性的关系
|
【零】
我始终认为,开始学习一门课程之前,首先要知道这门课程的实际用处或者为什么有这门课程,如果不了解这些,在学习的过程中往往会存在诸多疑问,也很难对这门课程产生兴趣,这也是我们推崇在实践中学习的原因。对于自动控制原理这门课程同样如此。 言归正传,对于自动控制系统的作用,我们以一个常见的例子“加热水”进行解释,如图1所示。 假设我们需要通过调节阀门(控制器输出)控制水管流出的水达到适合洗澡的温度(设定值),如果无法得知当前水温,想要达到目标,就需要通过复杂的数学分析建立完整的数学模型,从而计算得到阀门的开度,这就是一个开环系统。不难发现,开环系统对于构建的系统数学模型精度有较高的要求,而对于一些复杂的系统,系统数学模型往往很难精确建立,从而导致系统输出的精准性不高,另外,当系统受到外界扰动(如冷水流量变小)时则输出无法自动回到设定值。如果我在出水口检测水温,通过“大脑感觉”(控制算法)调节阀门的大小从而达到水温,如果水温高了,则使冷水多一些,水温低了,就使热水多一些,这就构成了一个闭环负反馈控制系统,这样的系统不需要较高的模型精确度(毕竟生活中我们洗澡时也不需要做繁琐的计算题),还具有较强的抗干扰性,即鲁棒性*(Robust)。系统加入反馈后,对于系统数学模型的精度要求就降低了,当然,越高的被控对象模型精度更有利于控制算法的设计。 通过这个例子,我们还可以解释一个初学者常见的误区:控制器的输出(如PI调节器)需要和控制器输入的单位(量纲)相对应吗?答案是不需要的。在上述例子中,控制器的输入是检测到的水温和设定水温的差值,输出则是阀门的开度,二者属于完全不同的物理量,只要控制算法和控制参数设计合理,控制器可以输出任意量纲的控制量。由此也可以体会到反馈的强大作用。 经过上述分析,我们还可以画出此系统的控制框图,如图2所示,这就是一个简单的闭环负反馈系统了。 现在,对于自动控制原理在实际中的应用我们已经有了初步的认识,这样的认识对于后续的学习至关重要。对于不同的被控对象,我们需要不同的控制算法进行控制,这也正是自动控制原理主要研究的内容,对于系统稳定性、动态响应、稳态误差等的研究基本都是为了辅助控制器/控制算法的设计,这也正是为什么我们要学习自动控制原理。 【壹】开门见山对于一个经典的控制系统而言,“稳、准、快”是评判系统性能的三个关键指标,分别表示系统输出是否能稳定(具体表现为在设定值对应频率下输出幅值保持不变),输出与设定值的差距(即稳态误差),输出达到稳定所需要的时间。其中,稳定性无疑是一个控制系统的首要指标,如果系统不稳定,则另外两个指标也无从谈起。在自动控制原理中,我们讨论最多的往往也是系统的稳定性,对于系统稳定性的分析也产生了各种各样的方法与结论,在刚开始学习的时候难免觉得有些混乱,本文将尝试从一个弹簧振动系统入手来简单分析系统稳定性及其相关结论,介绍微分方程和传递函数的联系与本质,同时也会穿插一些通过MATLAB工具简单分析系统的教程。 【贰】见微知著 对于图3所示的弹簧振动系统,初始时弹簧无拉伸或压缩,水平面光滑,则根据力的平衡原理,我们可以建立系统的数学模型:
F
(
t
)
−
k
x
=
m
a
\begin {equation}F(t) - kx = ma\end{equation}
F(t)−kx=ma可以进一步化为微分方程如下:
m
x
¨
+
k
x
=
F
(
t
)
\begin{equation}m\ddot{x}+kx=F(t)\end{equation}
mx¨+kx=F(t) 如果在初始时刻提供一个向右的位移
x
0
x_0
x0(或冲激力即初始速度
v
0
v_0
v0),则在无能量损耗的条件下物体将会保持固定的频率左右振动,如图4所示。 众所周知,弹簧的这种振动是一种简谐振动,接下来我们根据微分方程推导这种振动方式。系统平衡时的微分方程为: m x ¨ + k x = 0 \begin{equation}m\ddot{x}+kx=0\end{equation} mx¨+kx=0这是一个二阶常微分方程,特征方程为: m λ 2 + k λ = 0 m\lambda^2+k\lambda=0 mλ2+kλ=0。根据高数中二阶常系数线性微分方程的相关知识,当特征方程的根为共轭复根即 λ 1 , λ 2 = α ± j β \lambda_1,\lambda_2=\alpha\pm j\beta λ1,λ2=α±jβ时,其通解的形式为 e α t ( C 1 c o s β t + C 2 s i n β t ) e^{\alpha t}(C_1cos{\beta t}+C_2sin{\beta t}) eαt(C1cosβt+C2sinβt)。本例中特征方程的根为两个共轭虚数 ± j k m \pm j\sqrt{k\over m} ±jmk ,因此其解的形式则为 x = C 1 c o s k m t + C 2 s i n k m t \begin{equation}x=C_1cos{\sqrt{k\over m} t}+C_2sin{\sqrt{k\over m} t}\end{equation} x=C1cosmk t+C2sinmk t进一步可以化简为: x = 1 C 1 2 + C 2 2 s i n ( k m t + ϕ ) \begin{equation} x=\frac{1}{\sqrt {C_1^2+C_2^2}} sin({\sqrt{k\over m} t}+\phi)\end{equation} x=C12+C22 1sin(mk t+ϕ)即弹簧会以 f = w / 2 π = k m / 2 π f=w/2\pi=\sqrt{k\over m}/2\pi f=w/2π=mk /2π的频率做简谐振动,这个频率与初始时提供的位移或力无关,只取决于弹簧的弹性系数k和物体的质量m,称为系统的固有频率,而振动的幅值和相角则与系统的初始状态/初始输入相关,这与我们一般的认知相一致。为了便于求得幅值和初始相位,我们以式(4)作为讨论对象,假设系统初始时位移为 x 0 x_0 x0,初始速度为 v 0 v_0 v0,则有: { x 0 = C 1 c o s w t 0 + C 2 s i n w t 0 = C 1 x ˙ 0 = v 0 = − C 1 w s i n w t 0 + C 2 w c o s w t 0 = C 2 w \begin{equation} \begin{cases} x_0=C_1coswt_0+C_2sinwt_0=C_1\\ \dot{x}_0=v_0=-C_1wsinwt_0+C_2wcoswt_0=C_2w \end{cases} \end{equation} {x0=C1coswt0+C2sinwt0=C1x˙0=v0=−C1wsinwt0+C2wcoswt0=C2w由此可得物体任意时刻的位移为: x ( t ) = x 0 c o s k m t + v 0 w s i n k m t \begin{equation} x(t)=x_0cos\sqrt{k\over m}t+\frac{v_0}{w}sin\sqrt{k\over m}t \end{equation} x(t)=x0cosmk t+wv0sinmk t当只有初位移而没有初速度时: x ( t ) = x 0 c o s k m t \begin{equation} x(t)=x_0cos\sqrt{k\over m}t \end{equation} x(t)=x0cosmk t这也是我们最常见的情况了。 至此,我们完整地推导出了无阻尼弹簧振动系统在时域中的数学模型。事实上,这一部分内容与自动控制原理大部分时候研究的方式有所不同,对于本例相对简单的系统,通过解微分方程的方式可以清楚地获得系统每一时刻的输出,自然就获得了完备的信息,这也是最为直接的分析方法。然而凡事总是很难完美,对于更为复杂的系统,对应的微分方程阶数也越高,往往不易求解,常通过拉氏变换转到频域中分析,这也是后文的主要内容。然而,对于这种简单系统的时域分析依旧是需要了解的,毕竟,微分方程本质上与传递函数就是对应的关系,不理解微分方程,也就更无法理解传递函数了。 【叁】横峰侧岭 从不同的角度去看同一个事物往往会有截然不同的体会。前文我们已经介绍了在时域中对弹簧系统通过微分方程直接分析的方法,接下来,我们尝试从另一个角度去分析这个简单系统。如果我们把这个系统看成类似于【零】节中分析的控制系统,那么物体
m
m
m应为系统的被控对象,位移
x
x
x为系统的输出,而系统的控制器则为弹簧,它提供控制器的输出:弹力
F
k
F_k
Fk,控制算法为
F
k
=
−
k
x
=
k
(
0
−
x
)
F_k=-kx=k(0-x)
Fk=−kx=k(0−x),机智的朋友应该已经发现了,如果这个控制系统为单位负反馈系统(输出量即为反馈量),则这个控制系统的设定值/输入量为位移
x
0
=
0
x_0=0
x0=0。同理,类似于图2中的控制框图,我们也可以画出弹簧系统的框图如图5(a)所示,唯一不同的是系统中不需要传感器去测量输出量进行反馈。
对微分方程式(3)(假设无扰动力
F
(
t
)
F(t)
F(t)的作用)做拉普拉斯变换,可以得到:
m
s
2
X
(
s
)
−
m
s
X
(
0
)
−
m
X
˙
(
0
)
+
k
X
(
s
)
=
0
\begin{equation} ms^2X(s)-msX(0)-m\dot X(0)+kX(s)=0 \end{equation}
ms2X(s)−msX(0)−mX˙(0)+kX(s)=0由此我们可以得到系统输出的传递函数为:
X
(
s
)
=
[
s
X
(
0
)
+
X
˙
(
0
)
]
1
s
2
+
k
m
=
X
(
0
)
s
s
2
+
k
m
+
X
˙
(
0
)
k
m
k
m
s
2
+
k
m
\begin{equation} \begin{aligned} X(s)=[sX(0)+\dot X(0)]\frac{1}{s^2+\frac{k}{m}}\\ =X(0)\frac {s}{s^2+\frac{k}{m}}+\frac {\dot X(0)}{\sqrt\frac{k}{m}}\frac {\sqrt\frac{k}{m}}{s^2+\frac{k}{m}} \end{aligned} \end{equation}
X(s)=[sX(0)+X˙(0)]s2+mk1=X(0)s2+mks+mk
X˙(0)s2+mkmk
对上式进行反拉氏变换可以得到与式7完全一致的时域方程,上述推导得到了相互印证。这里进行的两个常见的拉氏反变换如图6所示。可以发现,上述推导结果和【贰】中的结果完全一致。图5(b)展示了此控制系统更完整的框图。 在上面的分析中,我们将系统的输入(设定值)视为位移0,而物体的振动来源于初始状态的非零,从控制系统的角度来理解,相当于一个物体(没有弹簧)具有一个初始的位移(位置),而我们通过向系统中加入一个弹簧控制器(弹簧自然长度时物体即在0位置上)试图控制物体在0位置上(虽然没有完全成功,但物体受到外力扰动时不至于远离此位置)。相反的,我们也可以把物体的初始位置定义为0(初状态为0),则加入的弹簧控制器的自然长度(输入/设定值)则决定了我们的控制目标,如图7所示。这样得到的结果与上述分析是一致的,读者可自行尝试推导。 上面的分析在理论上是没问题的,但与我们常规的认识又有些不同,现实中我们更习惯把外力F当作系统的输入,系统的输出仍旧是物体的位移,这显然也是可行的,对应的系统框图如图5(c)所示。不过,由于外力F通常不是我们想要控制的量,而是提供给系统的量,因此从自控的角度来看这不是一个典型的“控制系统”。这里其实也体现了自动控制的一种思想:实际应用中我们可以根据自己的需求选择控制量作为输入,例如在控制一个电机时,当我们想要控制电流大小不变时就以电流大小作为设定值,想要控制转速不变时就以转速作为设定值,甚至也可以同时反馈电流和转速,形成多环控制系统,这样的系统具有更强的稳定性,当然,设计难度也会更大一些。 【肆】 接下来我们重点分析弹簧振动系统的传递函数。在此之前,我们需要先清楚系统传递函数的定义:在零初始条件下,系统输出量的拉氏变换与输入量的拉氏变换之比。根据这个定义我们可以引申得出:在零初始条件下,系统单位冲激响应的拉氏变化即为系统传递函数。 再介绍一下通过控制框图求传递函数的方法。对于图8所示的典型闭环负反馈系统,开环传递函数为
W
(
s
)
H
(
s
)
W(s)H(s)
W(s)H(s),对于闭环传递函数的求解有:
C
(
s
)
=
W
(
s
)
E
(
s
)
E
(
s
)
=
R
(
s
)
−
H
(
s
)
C
(
s
)
\begin{equation} \begin{aligned} C(s)=W(s)E(s)\\ E(s)=R(s)-H(s)C(s) \end{aligned} \end{equation}
C(s)=W(s)E(s)E(s)=R(s)−H(s)C(s)由此可以推出系统闭环传递函数为:
W
B
(
s
)
=
W
(
s
)
1
+
W
(
s
)
H
(
s
)
\begin{equation} W_B(s)=\frac{W(s)}{1+W(s)H(s)} \end{equation}
WB(s)=1+W(s)H(s)W(s) 为了更贴近一个控制系统,同时,为了使初始状态为0,我们将物体初始位置视为0,因此选择图7进行分析,控制框图与图5(b)相同。由此可以求得弹簧振动开环传递函数为:
W
K
(
s
)
=
W
(
s
)
H
(
s
)
=
k
m
s
2
\begin{equation} W_K(s)=W(s)H(s)=\frac{k}{ms^2} \end{equation}
WK(s)=W(s)H(s)=ms2k 系统的闭环传递函数为:
W
B
(
s
)
=
W
K
(
s
)
1
+
W
K
(
s
)
=
k
m
s
2
+
k
m
\begin{equation} W_B(s)=\frac{W_K(s)}{1+W_K(s)}=\frac{\frac{k}{m}}{s^2+\frac{k}{m}} \end{equation}
WB(s)=1+WK(s)WK(s)=s2+mkmk对于这样一个二阶传递函数,它没有零点,极点可以由特征方程
s
2
+
k
m
=
0
s^2+\frac{k}{m}=0
s2+mk=0求得,显然,这与我们用微分方程分析得到的特征方程完全一致,也就是说,微分方程特征方程的根与传递函数的极点是相同的,因此我们之前的分析在这里也是适用的。即当闭环传递函数只具有一对共轭虚极点时,则系统输出将在设定值附近做等辐正弦振荡,即我们常说的临界稳定。 更进一步,当微分方程的特征根具有两个共轭复根的时候,其时域解为:
x
(
t
)
=
e
α
t
(
C
1
c
o
s
β
t
+
C
2
s
i
n
β
t
)
=
e
α
t
1
C
1
2
+
C
2
2
s
i
n
(
k
m
t
+
ϕ
)
\begin{equation} x(t)=e^{\alpha t}(C_1cos{\beta t}+C_2sin{\beta t})=e^{\alpha t}\frac{1}{\sqrt {C_1^2+C_2^2}} sin({\sqrt{k\over m} t}+\phi) \end{equation}
x(t)=eαt(C1cosβt+C2sinβt)=eαtC12+C22
1sin(mk
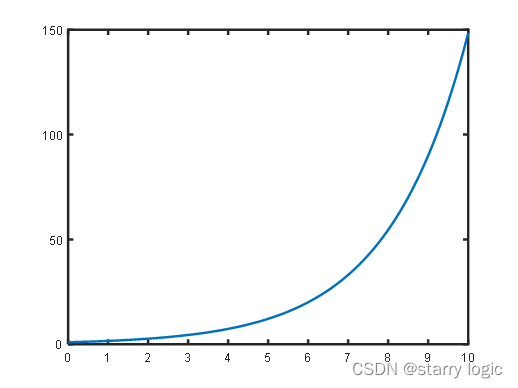
t+ϕ)可以相应地推出,当闭环传递函数具有一对共轭复极点时(通过拉氏反变换也可以得到),其时域解也是这个形式。可以看出,其时域表现由两部分组成,第一部分是实部引入的指数项,第二部分是虚部引入的三角函数项。显然,当
α
\alpha
α>0时,系统输出必然发散,当
α
\alpha
α
0
,
β
=
0
\alpha>0,\beta=0
α>0,β=0 |
【本文地址】










 C
1
C_1
C1
C
1
C_1
C1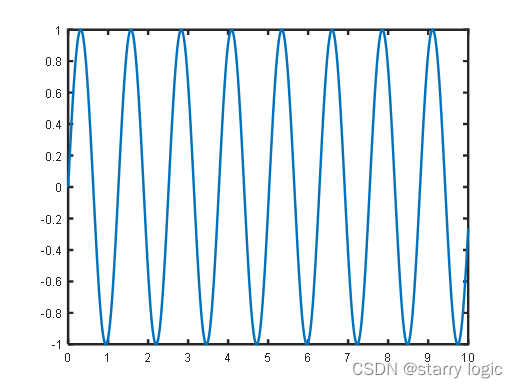
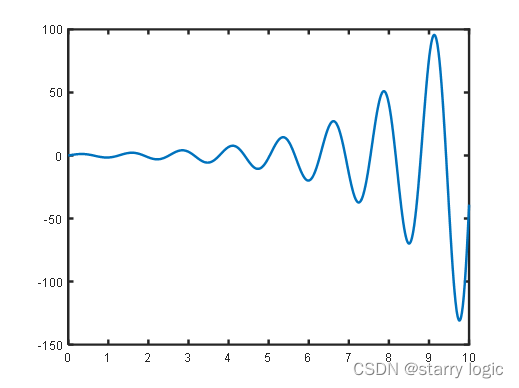 振荡发散
α
<
0
,
β
=
0
\alpha
振荡发散
α
<
0
,
β
=
0
\alpha