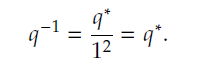| 【精选】四元数的定义与性质 | 您所在的位置:网站首页 › 二范数的定义是什么和什么 › 【精选】四元数的定义与性质 |
【精选】四元数的定义与性质
|
四元数
定义及性质模长(范数)四元数加减法四元数标量乘法四元数乘法Graßmann 积纯四元数逆和共轭
四元数的定义和复数非常类似,唯一的区别就是四元数一共有三个虚部,而复数只有一个。所有的四元数q∈H(H代表四元数的发现者William Rowan Hamilton)都可以写成下面这种形式: 与复数类似,四元数其实就是对于基{1,i,j,k}的线性组合,四元数也可以写成向量的形式。 仿照复数的定义,我们可以暂时将一个四元数q=a+bi+ci+dk的模长(或者说范数(Norm))定义为: 与复数类似,四元数的加法只需要将分量相加就可以了.如果我们有两个四元数q1=a+bi+cj+dk,q2=e+fi+gj+hk,那么它们的和为: 如果我们有一个四元数q=a+bi+cj+dk和一个标量s,那么它们的乘积为对应项系数相乘: 四元数之间的乘法比较特殊,它们是不遵守交换律的,也就是说一般情况 下q1q2 ≠ q2q1.这也就有了左乘和右乘的区别.如果是q1q2,那么我们就说 「q2 左乘以q1」,如果是q2q1,那我们就说「q2 右乘以q1」.除了交换律之外,我们经常使用的结合律和分配律在四元数内都是成立的。 那么,如果有两个四元数𝑞1 = 𝑎 + 𝑏𝑖 + 𝑐 𝑗 + 𝑑𝑘 和𝑞2 = 𝑒 + 𝑓 𝑖 + 𝑔𝑗 + ℎ𝑘,那么它们的乘积为: 利用上式表格,对四元数乘积的结果进一步化简: 对上述q1q2乘积结果进行重新整理如下所示: 写成有序对形式为: 如果一个四元数能写成这样的形式: 因为四元数是不遵守交换律的,我们通常不会将两个四元数相除写为𝑝/𝑞 的形式。取而代之的是将乘法的逆运算定义为𝑝𝑞−1 或者𝑞−1𝑝,注意它们的结果一般是不同的。 其中,𝑞−1 是𝑞 的逆(Inverse),我们规定: 我们定义,一个四元数𝑞 = 𝑎 + 𝑏𝑖 + 𝑐 𝑗 + 𝑑𝑘 的共轭为𝑞∗ = 𝑎 − 𝑏𝑖 − 𝑐 𝑗 − 𝑑𝑘(𝑞∗ 读作「q star」)。如果用标量向量有序对的形式来定义的话,𝑞 = [𝑠, v] 的共轭为𝑞∗ = [𝑠, −v]。 共轭四元数的一个非常有用的性质就是: |
【本文地址】
| 今日新闻 |
| 推荐新闻 |
| 专题文章 |
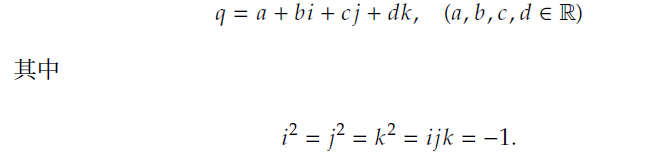 上面这个看似简单的公式就决定了四元数的一切性质。
上面这个看似简单的公式就决定了四元数的一切性质。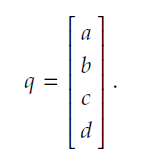 此外,我们在表示四元数时,还经常把实部与虚部分开,用一个实数s表示实部,用一个三维向量来表示虚部,将其表示为标量和向量的有序对形式:
此外,我们在表示四元数时,还经常把实部与虚部分开,用一个实数s表示实部,用一个三维向量来表示虚部,将其表示为标量和向量的有序对形式: 
 而如果用标量向量有序对的形式进行表示的话,q=[s,v]的模长为:
而如果用标量向量有序对的形式进行表示的话,q=[s,v]的模长为: 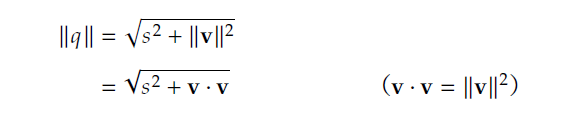 显然,四元数的模长很难用几何的方法来进行理解,因为它代表的是一个四维的长度.但是,和高维向量的模长一样,这只是类比复数模长进行衍生定义的结果,我们只需要将它理解为一个定义就可以了.。
显然,四元数的模长很难用几何的方法来进行理解,因为它代表的是一个四维的长度.但是,和高维向量的模长一样,这只是类比复数模长进行衍生定义的结果,我们只需要将它理解为一个定义就可以了.。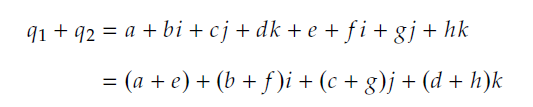 他们的差为:
他们的差为: 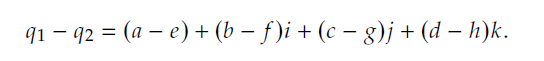 而对以标量向量有序对形式定义的四元数来说:q1=[s,v],q2=[t,u],那么:
而对以标量向量有序对形式定义的四元数来说:q1=[s,v],q2=[t,u],那么: 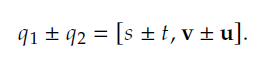
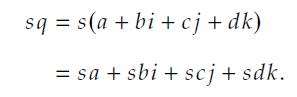 四元数与标量的乘法是遵守交换律的,也就是说sq=qs。
四元数与标量的乘法是遵守交换律的,也就是说sq=qs。 上式中的结果还是有点凌乱,我们根据博客开始的地方:
上式中的结果还是有点凌乱,我们根据博客开始的地方: 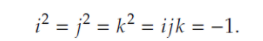 等到如下所示的表格:
等到如下所示的表格:  (其中有颜色的地方表示不能使用乘法交换律)
(其中有颜色的地方表示不能使用乘法交换律) 同时上式还可以简单的写成一个矩阵形式,如下所示:
同时上式还可以简单的写成一个矩阵形式,如下所示: 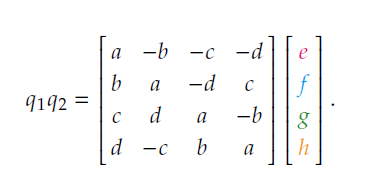 注意这个矩阵所做出的变换等价于左乘𝑞1.因为四元数不符合交换律,所 以右乘𝑞1 的变换是一个不同的矩阵,它可以使用完全相同的方法推导而得,结果如下:
注意这个矩阵所做出的变换等价于左乘𝑞1.因为四元数不符合交换律,所 以右乘𝑞1 的变换是一个不同的矩阵,它可以使用完全相同的方法推导而得,结果如下: 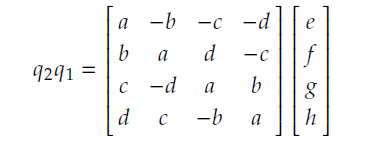
 令:
令:  那么:
那么: 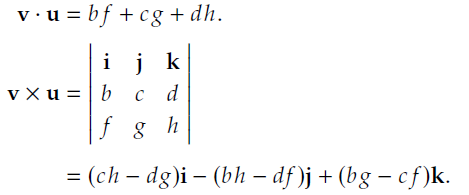 (注意:v × u的结果是一个向量,这里的i、j、k 是向量的基,写成这种形式结 果应该就非常清楚了,如果使用标量向量有序对形式来表示,q1 q2 的结果可 以用向量点乘和叉乘的形式表示出来)
(注意:v × u的结果是一个向量,这里的i、j、k 是向量的基,写成这种形式结 果应该就非常清楚了,如果使用标量向量有序对形式来表示,q1 q2 的结果可 以用向量点乘和叉乘的形式表示出来)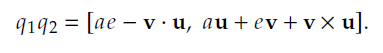 这个结果也被叫做Graßmann 积
这个结果也被叫做Graßmann 积 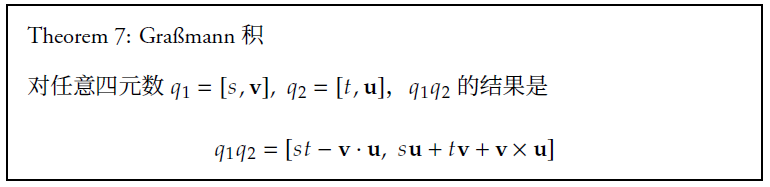
 那么我们则称𝑣 为一个纯四元数,即仅有虚部的四元数。 纯四元数有一个很重要的特性:如果有两个纯四元数𝑣 = [0, v], 𝑢 = [0, u], 那么:
那么我们则称𝑣 为一个纯四元数,即仅有虚部的四元数。 纯四元数有一个很重要的特性:如果有两个纯四元数𝑣 = [0, v], 𝑢 = [0, u], 那么: 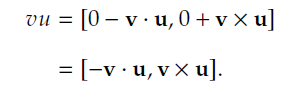
 这也就是说:
这也就是说:  显然,要在无数的四元数中寻找一个满足𝑞𝑞−1 = 𝑞−1𝑞 = 1 的𝑞−1 是非常困难的,但是实际上我们可以使用四元数共轭的一些性质来获得𝑞−1。
显然,要在无数的四元数中寻找一个满足𝑞𝑞−1 = 𝑞−1𝑞 = 1 的𝑞−1 是非常困难的,但是实际上我们可以使用四元数共轭的一些性质来获得𝑞−1。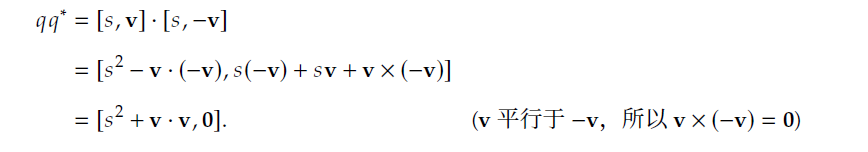 可以看到,这最终的结果是一个实数,而它正是四元数模长的平方:
可以看到,这最终的结果是一个实数,而它正是四元数模长的平方: 
 所以:qq* = q*q,满足乘法交换定律。 引入之前定义的四元数逆,qq-1 = 1。
所以:qq* = q*q,满足乘法交换定律。 引入之前定义的四元数逆,qq-1 = 1。  用这种办法寻找一个四元数的逆会非常高效,我们只需要将一个四元数的虚 部改变符号,除以它模长的平方就能获得这个四元数的逆了.如果∥𝑞∥ = 1, 也就是说𝑞 是一个单位四元数(Unit Quaternion),那么
用这种办法寻找一个四元数的逆会非常高效,我们只需要将一个四元数的虚 部改变符号,除以它模长的平方就能获得这个四元数的逆了.如果∥𝑞∥ = 1, 也就是说𝑞 是一个单位四元数(Unit Quaternion),那么