| 微积分基础 | 您所在的位置:网站首页 › 乘法函数求导公式 › 微积分基础 |
微积分基础
|
几何角度解释物理角度解释
生理上知道如何画出切线,步骤为--先形象化几何问题,然后大脑就会找出答案,现在我们要从数学机理上分析人是以什么步骤画出切线的。 1. 瞬时变化率平均变化率-平均速度 瞬时变化率-瞬时速度 从平均速度引入瞬时速度比较合适。举例,对于平均速度来说,当时间差接近0时,平均速度就变成了瞬时速度 平均速度又等于两点的斜率,当时间差接近0时,斜率(瞬时斜率)又等于曲线切线的斜率,因此曲线切线的斜率就是瞬时速度 利用无限小增量的方式,就能得到某点的瞬时斜率
斜率就是两点之间的平均变化率 不指明方向叫速率,指明方向叫速度 2. 极限和连续 2.1 极限极限是微积分的基础,尽管它非常重要,却是一个很简单的概念。极限又分为左极限和右极限。通常情况下,x 是变量,但对于极限情况,x 固定不变,Δx 是变量 定义(epsilon delta definition):对于给出的任何大于0的ε,无论ε等于多少,都存在一个大于0的Δ,使得当0 瞬时变化率: 例子1(将x考虑为时间): 例子2(将x考虑为海拔高度)
求导公式分两种:对特定函数的求导、通用的求导法则 3.1. 特定函数的求导求多项式、指数对数、三角函数等的导数 1. 幂函数的导数(n 为有理数) 2. 三角函数 3. 指数和对数函数 证明(没有按照上面的顺序) 1.
2. 证明1,已知 e 的定义(复利引入了e的定义)的情况下:
3. 使用链式法则求导: 又因为: 所以:
4. 此处为换底法,也可以使用对数微分法 5. 上面的证明过程利用了“极限与连续”中的结论 3.2. 通用的求导法则求导四则运算(加法法则,乘除法则),常乘数法则,链式法则,隐式函数微分法,对数微分法 证明 1. 乘法法则(多变量微积分的链式法则也可以证明该法则) 2. 除法法则证明过程类似于乘法法则 3. 链式法则 链式法则是一个合成规则,核心思想是换元法,掌握了链式法则,你能征服世界 举例 隐式函数微分法:对于一个等式,不需要解出未知的函数,直接对等式两边微分的方法,称为隐式函数微分法 链式法则是非常给力的技巧,而隐函数微分则是一种更巧妙的代数方法,不用将等式表示成函数,因此叫“隐函数”。事实上,显式函数方法和隐式函数方法都可以用。隐式函数微分法主要用于求导任意反函数,只要知道原函数的导数就行。 例子1 因为 y 是 x 的函数,运用链式法则: 将 y 带回去: 对数微分法是处理指数函数的一个典型方法 例子(?有点循环证明的味道) 证明: 线性近似,二阶近似,曲线画图,牛顿迭代法,中值定理 4. 微分、积分 定义:如果有一个函数 y = f(x),那么 y 的微分记做 dy ,且定义为 dy = f'(x) dx 。两边同时除以 dx ,就是导数的定义。该记法的思想是用 dx 代替 Δx,dy 代替 Δy 反导函数定义(由微分的定义引出): 大 G(x) 为小 g(x) 的反导函数,又称不定积分。为什么称为不定积分?是因为 C 无法确定,因此无法给出一个确定的函数 积分唯一性: 事实上,积分比求导难很多,有时甚至积不出来,所以积分有很多技巧,例如变量代换
特定函数的反导 多项式、三角函数,指数对数的反导,以及其它函数的反导(三角代换) 通用的反导法则(积分法则) 加法、常乘数、反乘法法则,反乘法法则又推导出了分部积分,反链式法则,定积分性质,部分分式展开(拉普拉斯变换中也有此方法,即把函数转换为容易积分的分式)
分部积分(比反乘法法则更有用,每进行一次,f(x)的指数会降低一次): 反链式看不出来的话,可以使用变量代换 定积分性质:
微分应用--微分方程 微分方程:包含微分的方程称为微分方程 注意:传统方程的解是一个数字,微分方程的解是一个函数 例1
例2 4.1. 如何理解定积分 定积分有多种理解方式,其中一种就是“曲线下的面积” 从几何上讲,积分只是“对许多宽很小的矩形面积求和”,精确地说,x 轴上方的面积减去 x 轴下方的面积 导函数曲线下的面积等于原函数两个函数值的差,因此可以利用积分求曲线下的面积:
假设“时间距离方程”及其导函数“时间速率方程”为:
通过“时间距离方程”求1秒到2秒经过的距离: 通过“时间速率方程”求1秒到2秒经过的距离: 当δt趋于0时,通过“时间速率方程”求得的距离近似等于“时间距离方程”的结果。 又因为: 为导函数曲线下的一系列长方形的面积,因此如果想求某个曲线下的面积,可以先对曲线积分,然后利用积分求得曲线下的面积 进一步扩展,可以利用积分思想求旋转体的体积(圆盘方法,壳方法)。
假设导函数沿x轴旋转,旋转体的体积(圆盘方法)为:
假设导函数沿y轴旋转,旋转体的体积(壳方法)为:
三角换元法隶属于换元法 将Θ代回去: 例2: 根据 m,n 奇偶的情况,计算方法不同 4.2.2. 分部积分
证明: 5. 微积分第一定理 该式子又称为微积分第一定理 应用:求曲线长度,曲线下的面积,体积,平均值(离散平均值,连续平均值,加权平均值),概率等;直线,圆等的长度都可以用微积分思想来求 例1: 离散平均值 -> 连续平均值 比如点在半圆上的平均高度(对 dx 计算平均值):
另一种平均高度(对 dθ 计算平均值):
例2: 加权平均值(weighted average) 解释1:假设 f(x)=C ,分母必须等于权重的积分 解释2:假设第一次买某股票的价格为 f1,买了 w1 股,第二次价格为 f2,买了 w2 股,依次类推,买股票的平均价格为: 例3: 数值积分:黎曼和、梯度法、辛普森公式 如何将问题演变成数学问题? 很多概率问题都符合: 5.1 微积分第一定理与中值定理的比较 要想理解 Ave(f) ,可以假设积分时 dx 的宽度为1,然后从离散值求平均的概念进行理解 而中值定理为: 其中,c 在定义域内是不确定的,只知道 a < c < b,也就是说不知道 c 究竟是哪一点,它比较笼统和简单 而 Ave(F') 是确定值,因此微积分基本定理比中值定理“强”,只要能用积分,就应尽量避免使用中值定理 6. 微积分第二定理 微积分第二定理的意思是,一个函数能够找到其相应的积分形式 当一个函数由上述积分形式给出时,先通过其一阶、二阶导数作图,因为了解一个函数,最直观的办法就是画图 证明:
应用:解微分方程 例1: 但 L(x) 的积分形式为: 例2:
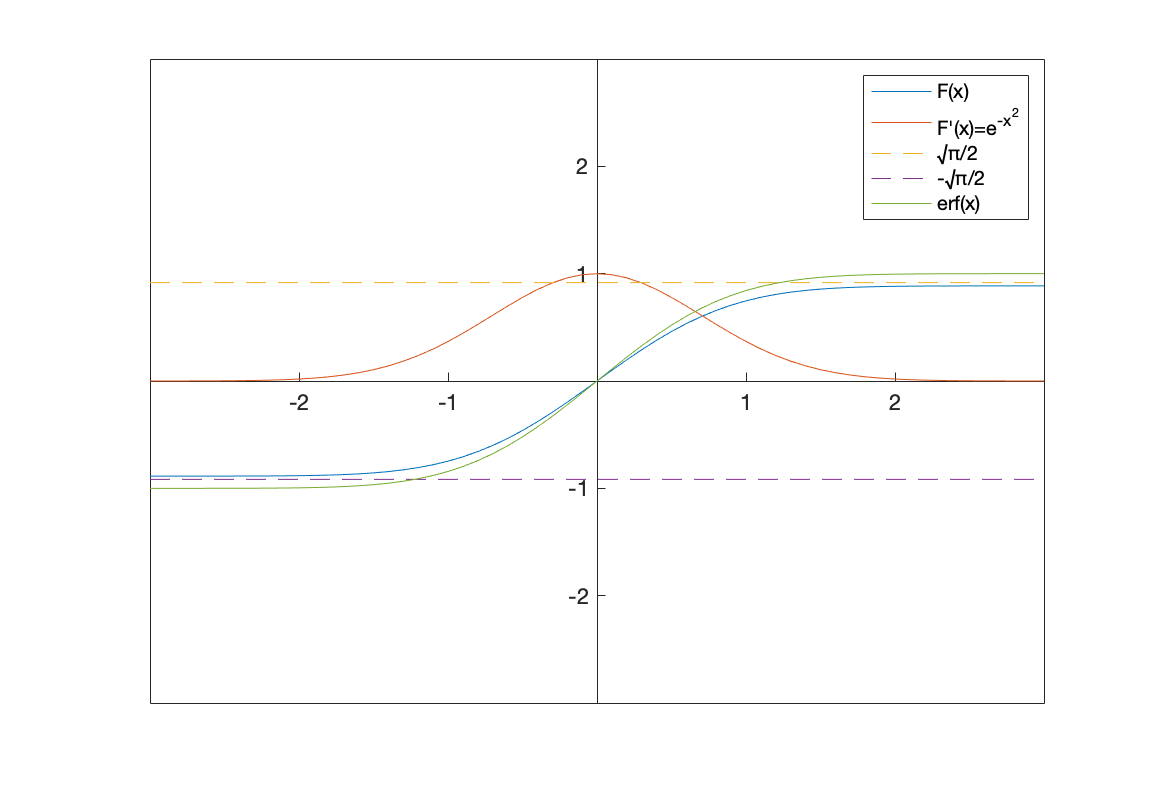
F' 为有名的钟形曲线 bell curve,它是从概率论得出的(概率就是部分与整体的比值);F(x) 则为 F' 曲线下的面积 由数值 |
【本文地址】