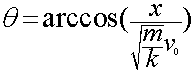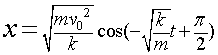| 简谐振动基本方程的推导 | 您所在的位置:网站首页 › 三角分布推导公式过程图 › 简谐振动基本方程的推导 |
简谐振动基本方程的推导
|
——本博客为博主原创,如有雷同,纯属巧合,未经允许,不得抄袭 简谐振动,作为自然界极为常见的运动方式,具有简洁而数学化的美妙,而对于简谐运动的公式: 首先,我们可以构建这样一个模型(如下图所示),在一根无限长的数轴上,有一个运动的质点。若t为运动时间,当t=0时,质点具有初速度v0,不妨假设速度的方向为数轴正方向,当质点运动到位置x时,质点所受到的力为: 现在,我们来推导这个公式。经过实际试验,我们发现直接去推导这个x显得尤为困难,这时候,我们反过来思考,求出t的表达式。 首先,我们先计算出任意时刻质点的机械能
在上式中,Ek 表示质点此时具有的动能,Ep 表示质点此时具有的势能,v表示物体的速度,由于这个模型实际上与弹簧模型极其近似,我上述公式的推导不再呈现。 当然,质点满足机械能守恒,由此,我们又有: 联立1式,我们可以解出v来: 仔细观察上式,我们发现,组成这个乘积两部分的第二部分很接近于直角三角形勾股定理表达式 图中,AB的长度为
为了能够为后面的计算准备,我们干脆也把x给重写一下,为:
现在,我们求出了v,下面就可以求出t了。根据速度的定义,可以写出如下式子
将2、3式代入,得到: 从中解出dt来
在上式的计算过程中,博主使用了公式dcos(θ)=sin(θ)dθ,读者可以自行查找。 既然得到了dt,我们就可以两边从t=0到t=t积分,进而求出t(注意:当t=0时,θ的值为π/2):
现在,我们已经求得了t。为了求出x,我们再次利用3式,用x表示θ,得:
代入4式,通过计算,解出x
该式与简谐振动的基本方程一致,由此证毕。
|
【本文地址】
| 今日新闻 |
| 推荐新闻 |
| 专题文章 |
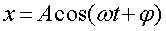 的推导过程,一直是比较复杂的一个问题。博主通过自己的思考,得出了一种比较简洁的方法。
的推导过程,一直是比较复杂的一个问题。博主通过自己的思考,得出了一种比较简洁的方法。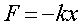 其中,负号表示质点所受力的方向与位置矢量方向相反,在这次推导中,由于一切运动是一维的,我们可以就此用有正负的标量表示运动的度量。
其中,负号表示质点所受力的方向与位置矢量方向相反,在这次推导中,由于一切运动是一维的,我们可以就此用有正负的标量表示运动的度量。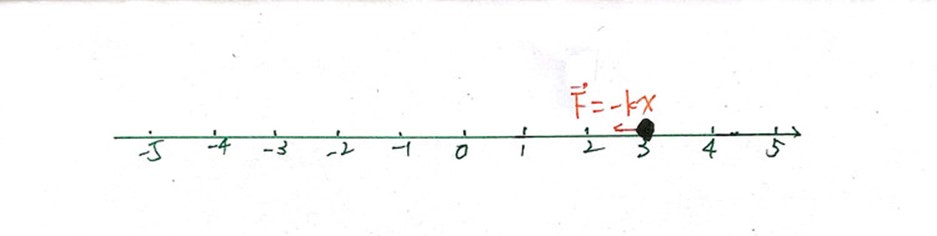
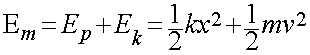 —————————1
—————————1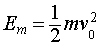
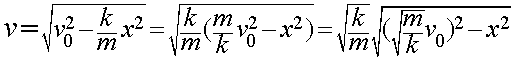
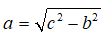 。由此,基于上面的数轴,我们在做一直角三角形,如下:
。由此,基于上面的数轴,我们在做一直角三角形,如下: 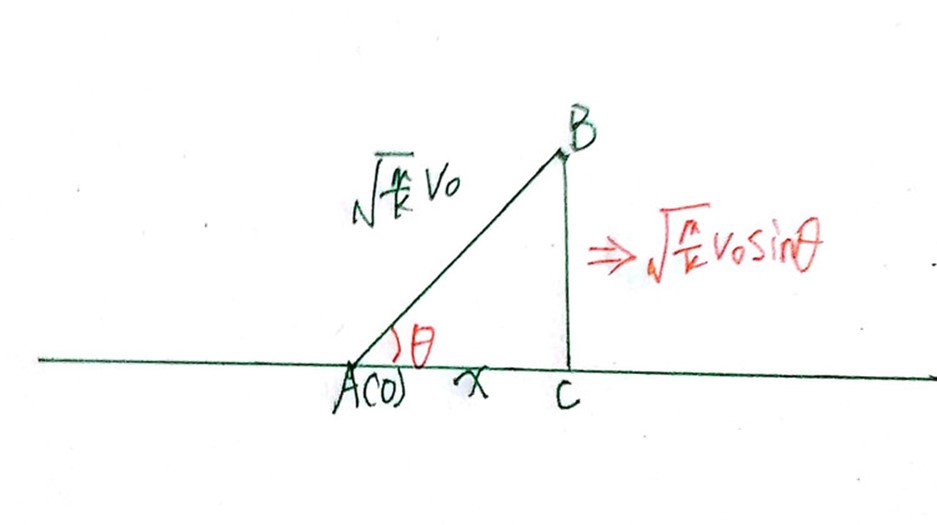
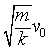 AC的长度为x,观察上式,可以发现第二项所提到的内容等于BC的长度,假设∠BAC为θ,重写该项为
AC的长度为x,观察上式,可以发现第二项所提到的内容等于BC的长度,假设∠BAC为θ,重写该项为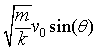 ,则BC的长度变为:
,则BC的长度变为: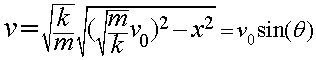 ———————2
———————2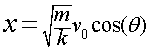 ———————3
———————3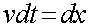
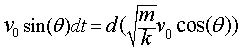
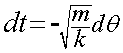
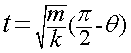 ——————————————4
——————————————4