| 直观理解导函数(直接画出导函数的图像) | 您所在的位置:网站首页 › y=x2的图像是什么 › 直观理解导函数(直接画出导函数的图像) |
直观理解导函数(直接画出导函数的图像)
|
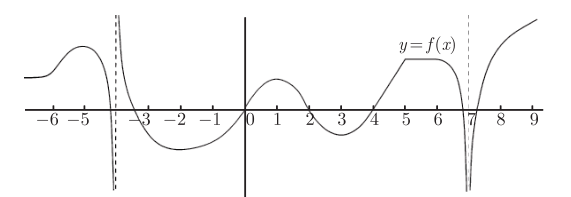
本例来自《普林斯顿微积分》,和朋友们分享~ 假设有一个函数的图像, 你不知道它的方程, 但又想要画出其导函数的图像。这时公式和法则帮不上你, 你需要的是对微分有一个很好的理解。 下面是基本思想:将函数的图像想象成一座山, 并想象有一个小登山者在从左到右地爬上爬下。在攀登的每一点上, 登山者会大声地喊出他认为攀登有多困难。如果地形平坦, 登山者会大声喊出数 0 以表示难度。如果地形呈现向上的斜坡, 登山者会大声喊出一个正的数; 攀登越陡峭, 数越大。如果地形呈现向下的斜坡, 那么攀登实际上很轻松, 因此难度是负的。也就是说, 登山者会大声喊出一个负的数。向下的斜坡越陡越轻松, 因此数会越来越负。( 如果下坡确实非常陡, 那它或许会让下行变得更不安全, 但它显然也让下降变得更为快速 !)这里的要点是:山的高度本身不重要, 重要的是陡峭程度。特别地, 你可以将整个图像向上平移, 登山者还是会大声喊出相同的难度程度来。这意味着, 如果你从一个函数的图像画一个导函数的图像, 该函数的y轴截距是不重要的! 来看一个例子:画出下述让人恐惧的函数的导函数的图像, 如图所示。
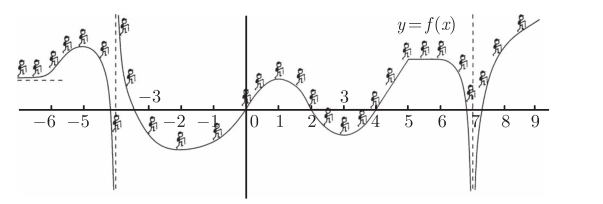
不要惊慌。需在各个不同的点上画一个小登山者并想象登山者在每一点上大声喊出难度程度。然后 , 你所要做的就是在另一套坐标上画出这些难度程度。特别要留心的是那些路径平坦的点; 这可以出现在一个长的平坦的区域中 ( 如上图中的x=5和x=6之间 ), 或者在一个峰的顶部 ( 如在x=−5或x=1), 又或者在一个谷的底部 ( 如在x=−2或x=3)。那里你肯定是要画出登山者的。下图是在一些位置放上登山者的 f 的图像:
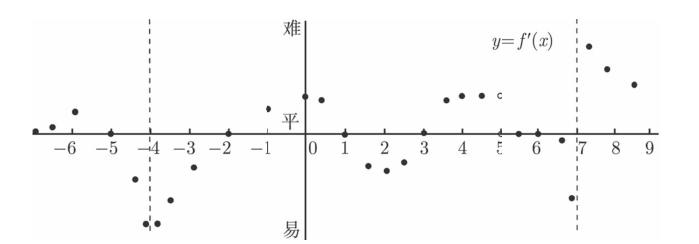
现在, 为导函数的图像来画一套坐标。y 轴标记为 “ 难度程度 ”, 从上至下由难至易。然后, 基于小登山者大声喊出的难度程度, 你应该能够用铅笔描出一些点来。回想一下, 登山者并不关心山有多高, 他只关心山有多陡! 基于此, 会得到下图上的一些点:
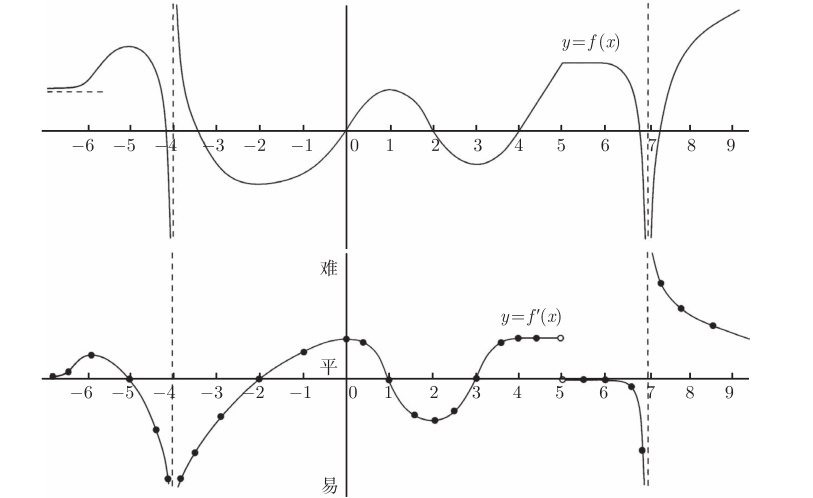
以下是对于如何得出这些点的详细解释: • 在y=f(x)的图像的最左侧, 登山者开始只是缓缓地上坡。因此, 将画出一些高度稍高于 0 的一些点。 • 往前走, 走到x=−6, 登山者开始上坡, 因此难度上升, 这些点也变高了 ( 更难了 )。 • 然后 , 开始变得略微容易点, 直到x=−5时, 登山者达到峰的顶部, 那里是平坦的。特别地, 当x=−5时, 导函数有一个x轴截距。 • 在x=−5之后, 原始函数的曲线开始变成下坡, 首先较为平缓, 然后越来越陡。这意味着, 攀登将变得越来轻松, 直到它变得非常非常轻松。因此, 导函数在x=−4处有一条垂直渐近线。 • 在该渐近线的另外一侧, 攀登也很容易, 因为登山者将下坡, 开始非常陡, 并在x=−2处到达谷底。因此, 在导函数曲线上, 垂直渐近线实际上始于−∞( 非常非常容易 ) 并在x=−2处爬升至 0。( 在x=−5和x=−4之间有x轴截距以及在x=−4 和x=−3之间也有, 但这都无关紧要。原始函数的x轴截距不重要。) • 在x=−2到达谷底之后 , 登山者必须上坡一会儿, 因此攀登变困难了。尽管在x=0之后变得略微容易点 , 但他依然要往上爬, 直到x=1的山顶。这意味着, 导函数的曲线上升, 直到x=0, 然后下降 , 直到x=1, 得到一个x轴截距。 • 在走向x=3处谷底的路上, 情况发生了逆转:下坡越来越陡, 直到 x=2,然后坡度减缓些, 但仍然是下坡。因此, 导函数的曲线下降, 在x=2处达到一个最小值, 然后上升, 直到 x=3, 得到一个 x 轴截距。 • 从x=3处的谷底起, 攀登一直都很困难, 直到x=4。然而, 在x=4 和x=5之间, 攀登的难度是均匀的, 因为斜率是常数。因此, 导函数的曲线从x=3上升, 直到 x=4, 然后在x=4 和 x=5之间, 保持在同一高度 ( 难度程度 )。 • 在x=5, 斜率突然地改变了。在没有任何预警的情况下, 它突然变平坦了,然后保持这种平坦直到x=6。因此, 导函数的曲线必须下降至 0 并且保持为 0 直到x=6。导函数在x=5处有一个不连续点。 • 在x=6之后, 登山者发现 , 随着曲线逼近x=7处的垂直渐近线 , 攀登越来越容易了。导函数的曲线在那里也有一条垂直渐近线。 • 在这条垂直渐近线的右侧, 攀登极度困难, 但当x走向9时, 攀登变得略微容易点。因此, 导函数的曲线在x=7的右侧始于非常高的地方, 然后当攀登越来越容易时, 它变得越来越低。 现在, 只需要把这些点连起来 ! 下图分别是 y=f(x) 和 y=f′(x) 的图像:
我们把所用的思想做一下总结。 • 当原始图像平坦时, 导函数的图像有一个x轴截距。在上例中, 它们出现在x=−5, x=−2, x=1, x=3及区间 [5,6] 的每一点上。 • 当原始图像的一部分是一条直线时, 导函数的图像是常数 ( 上例中, 它出现在区间 [4,5] 上 )。 • 如果原始图像有一条水平渐近线, 其导函数图像经常也有一条水平渐近线,但如果是那样的话, 它将在y=0的高度, 而不是渐近线的原始高度上 ( 正如上例中图像的左端 )。 • 原始图像中的垂直渐近线通常导致导函数在相同位置上也有垂直渐近线尽管方向可能会改变。例如上例中, 在x=7处, 在渐近线的两侧, 原始函数的曲线都走向−∞, 但导函数却有相反的符号。在x=−4处的垂直渐近线也受到类似的影响。 如果有怀疑的话, 就请使用那些值得信赖的登山者进行验证吧! |
【本文地址】