Romberg 学习笔记

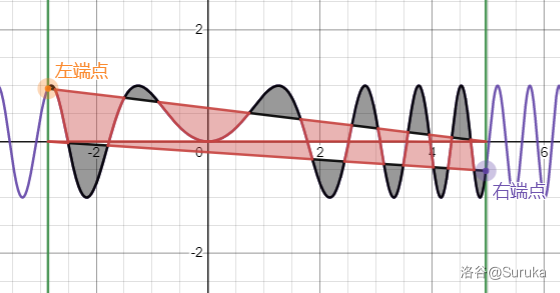
本文遵守 署名-非商业性使用-禁止演绎 4.0 协议，转载请带上著名，并按原样转载。

本文章主要讲解龙贝格算法与推导过程(Romberg's Method)，同时作为 P4526，UVA1356，P4207 的题解。

如果您不想看推导，请跳至 0x16；如果您是从题解区进来的，请在阅读完 0x1 的所有内容后跳至 0x3 的对应题目。

对于下文中出现的每个未定义的函数 $f(x),g(x)$ 等，除非有特别说明，否则默认其在区间 $[a,b]$ 内可积，且对于每个小标题均非同一函数。

如果您刚入门，请在看完本节后直接跳至 0x16，否则您可以跳过本节。

微分 $f'(x) / \mathrm{d}f(x)$，就是 $f(x)$ 在某一瞬时的变化量。

积分 $\int_a^bf(x)\mathrm{d}x$，就是求 $f(x),x=a,x=b,y=0$ 围成图形的面积，$y=0$ 上面为正，下面为负。

数值积分，就是对于某些特别难求的积分，通过某些方法逐步逼近准确值。

优点：收敛性能良好；在许多题目上运行快速；思路清晰，显然比自适应辛普森积分的 $\times15$ 好写；非递归，占用内存相对较小。

缺点：有多种写法且代码难度与复杂度差异巨大；对于在积分区间中具有不同平稳性来回变化的函数具有较差的性能（这个缺点是非自适应性数值积分算法所共有的，但是对于龙贝格算法来说，它收敛快速的优点事实上基本抵消了这个缺点）。

而且它不仅可以做微积分题，还可以水过某些计算几何毒瘤题，并且好想好写。

我们知道，有梯形公式 $\int_a^bf(x)\mathrm{d}x\approx\frac{(f(a)+f(b))(b-a)}{2}\kern{25px}(1)$。

则在给定 $n$ （$n$ 为分点个数）的情况下由 $(1)$ 得复化梯形求积公式：

$$\int_a^bf(x)\mathrm{d}x=\sum_{k=0}^{n-1}\int_{x_k}^{x_{k+1}}f(x)\mathrm{d}x\approx\sum_{k=0}^{n-1}\frac{a-b}{2n}(f(x_k)+f(x_{k+1}))$$

$$=\frac{b-a}{2n}(f(a)+f(b)+2\sum_{k=1}^{n-1}f(x_k))\kern{25px}(2)$$

其中 $x_k=a+k\cdot\frac{b-a}{n}$。

假定某一函数 $f$ 可数值近似为 $F(h)$，其中 $h$ 为步长，

$f=F(h)+ah^{p}+bh^{q}+\ldots\kern{25px}(3)$

其中 $p$ 为首项阶数，$q$ 为下一项阶数，满足 $q>p$。

同样地，我们有

$f=F(h_{2})+ah_{2}^{p}+bh_{2}^{q}+\ldots\kern{25px}(4)$

则由 $(3)-({\frac {h}{h_{2}}})^{p}(4)$ 得：

$$(1-r)f=F(h)+ah^{p}+bh^{q}-rF(h_{2})-rah_{2}^{p}-rbh_{2}^{q}+\ldots=F(h)-rF(h_{2})+a\underbrace{(h^{p}-rh_{2}^{p})}_{0}+b(h^{q}-rh_{2}^{q})$$

$$(1-r)f=F(h)-rF(h_{2})+b(h^{q}-rh_{2}^{q})$$

$$f={\frac{F(h)-rF(h_{2})}{1-r}}+{\frac{b(h^{q}-rh_{2}^{q})}{1-r}}={\frac{F(h)-rF(h_{2})}{1-r}}+{\frac{b(1-r{\frac{h_{2}^{q}}{h^{q}}})h^{q}}{1-r}}$$

$$f={\frac{F(h)-rF(h_{2})}{1-r}}+{\frac{b(1-({\frac{h}{h_{2}}})^{p}({\frac{h_{2}}{h}})^{q})h^{q}}{1-r}}=\underbrace{\frac{F(h)-rF(h_{2})}{1-r}}_{f^*(h)}+\underbrace{\frac{b(1-({\frac{h_{2}}{h}})^{q-p})}{1-r}}_{b^*}h^{q}$$

其中 $r=({\frac {h}{h_{2}}})^{p}$。

所以，我们得到更高精度的函数 $F^*(h)=\frac{F(h)-\left({\frac {h}{h_{2}}}\right)^{p}F(h_{2})}{1-\left({\frac {h}{h_{2}}}\right)^{p}}\kern{25px}(5)$。

先放张图直观地感受一下梯形公式的误差。

如图 1 所示，红色部分为多算部分，黑色部分为少算部分。

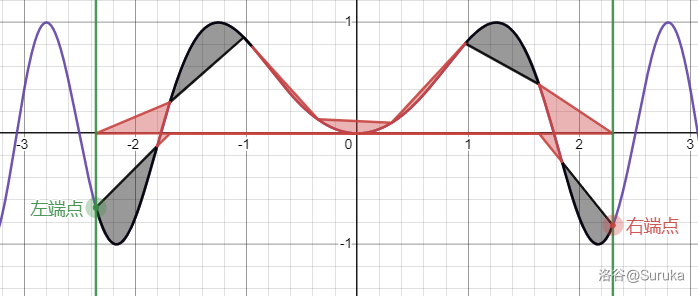
$$\tiny\color{grey}\text{图~1，梯形公式的误差，原创}$$

由分部积分法 $\int g'(x)f(x)\mathrm{d}x = g(x)f(x)-\int g(x)f'(x)\mathrm{d}x$ 得，

$$\int_a^b g'(x)f(x)\mathrm{d}x = g(b)f(b)-g(a)f(a)-\int_a^b g(x)f'(x)\mathrm{d}x$$

$$\therefore\int^b_a f(x)\mathrm{d}x=\int^b_a1\cdot f(x)\mathrm{d}(x-a)$$

$$=(b-a)f(b)-(a-a)f(a)-\int_a^b(x-a)f'(x)\mathrm{d}(x-a)=(b-a)f(b)-\int_a^b(x-a)f'(x)\mathrm{d}x\kern{25px}(6)$$

同理，

$$\int^b_a f(x)\mathrm{d}x=(b-a)f(a)-\int_a^b(x-b)f'(x)\mathrm{d}x\kern{25px}(7)$$

由 $\frac{(6)+(7)}{2}$ 得，

$$\int^b_a f(x)\mathrm{d}x=\frac{(f(a)+f(b))(b-a)}{2}-\frac{\int_a^b((x-a)+(x-b))f'(x)\mathrm{d}x}{2}$$

$$=(1)-\frac{\int_a^b((x-a)+(x-b))f'(x)\mathrm{d}x}{2}$$

我们可以发现，$((x-a)(x-b))'=(x-a)'(x-b)+(x-a)(x-b)'=(x-b)+(x-a)$，所以设 $u=(x-a)(x-b)$。

$$\int^b_a f(x)\mathrm{d}x=(1)-\frac{\int_a^b((x-a)+(x-b))f'(x)\mathrm{d}x}{2}=(1)-\frac{\int_a^bu'f'(x)\mathrm{d}u}{2}=(1)-\frac{\int_a^b1\cdot f'(x)\mathrm{d}u}{2}$$

再由分部积分法得，

$$\int^b_a f(x)\mathrm{d}x=(1)-\frac{\int_a^b1\cdot f'(x)\mathrm{d}((x-a)(x-b))}{2}$$

$$=(1)-\frac{(b-a)(b-b)f'(b)-(a-a)(a-b)f'(a)-\int_a^b(x-a)(x-b)f''(x)\mathrm{d}((x-a)(x-b))}{2}$$

$$=(1)+\frac{\int_a^b(x-a)(x-b)f''(x)\mathrm{d}((x-a)(x-b))}{2}=(1)+\frac{\int_a^b(x-a)(x-b)f''(x)\mathrm{d}x}{2}$$

再由定积分第一中值定理 $\exists\xi\in[a,b],\int_a^bf(x)g(x)\mathrm{d}x=f(\xi)\int_a^bg(x)\mathrm{d}x$ 得，

$$\exists\xi\in[a,b],\int^b_a f(x)\mathrm{d}x=(1)+\frac{\int_a^b(x-a)(x-b)f''(x)\mathrm{d}x}{2}=(1)+\frac{f''(\xi)}{2}\int^b_a(x-a)(x-b)\mathrm{d}x$$

我们着手计算 $\int^b_a(x-a)(x-b)\mathrm{d}x$，先设 $v=\frac{x-a}{b-a}$，则 $x=(b-a)v+a$，即 $(x-a)=(b-a)v,(x-b)=(b-a)v+(a-b)=(b-a)(v-1)$。

$$\therefore\int^b_a(x-a)(x-b)\mathrm{d}x=\int^b_a(b-a)^2v(v-1)\mathrm{d}x=\int^b_a(b-a)^3v(v-1)\mathrm{d}v$$

$$=(b-a)^3\int^b_a(v^2-v)\mathrm{d}v=(b-a)^3(\int^b_av^2\mathrm{d}v-\int^b_av\mathrm{d}v)=(b-a)^3(\frac{1}{3}-\frac{1}{2})=-\frac{1}{6}(b-a)^3$$

由此得

$$\exists\xi\in[a,b],\int^b_a f(x)\mathrm{d}x=(1)+\frac{f''(\xi)}{2}\int^b_a(x-a)(x-b)\mathrm{d}x=(1)-\frac{f''(\xi)(b-a)^3}{12}\kern{25px}(8)$$

即梯形公式的余项公式（误差）为 $-\frac{f''(\xi)(b-a)^3}{12}$。

同样先放张图直观地感受一下复化梯形求积公式的误差。

如图 2 所示，红色部分为多算部分，黑色部分为少算部分。

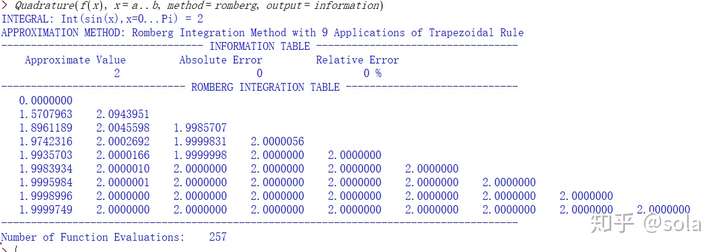
$$\tiny\color{grey}\text{图~2，复化梯形求积公式的误差，原创}$$

$$\int^b_a f(x)\mathrm{d}x-(2)=\sum_{k=0}^{n-1}\int_{x_k}^{x_{k+1}}f(x)\mathrm{d}x-\sum_{k=0}^{n-1}\frac{a-b}{2n}(f(x_k)+f(x_{k+1}))$$

我们可以发现上式第二个 $\sum$ 的后面即为当 $a=x_k,b=x_{k+1}$ 时的梯形公式。

则可以由 $(8)$ 得，

$$\int^b_a f(x)\mathrm{d}x-(2)=\sum_{k=0}^{n-1}{\huge(}\int_{x_k}^{x_{k+1}}f(x)\mathrm{d}x-\frac{b-a}{2n}(f(x_k)+f(x_{k+1})){\huge)}=-\frac{1}{12}\sum_{k=0}^{n-1}f''(\xi_k)(x_{k+1}-x_k)^3$$

$$=-\frac{(b-a)^3}{n^3}\cdot\frac{1}{12}\sum_{k=0}^{n-1}f''(\xi_k)=-\frac{(b-a)^2}{n^2}\cdot(b-a)\cdot\frac{1}{12}\sum_{k=0}^{n-1}\frac{f''(\xi_k)}{n}$$

因为 $f''(x)$ 在区间 $[a,b]$ 上连续，所以 $f''(x)$ 在区间 $[a,b]$ 上有最大值 $\textit{fmax}$ 与最小值 $\textit{fmin}$，则 $n\cdot\textit{fmin}\le\sum_{k=0}^{n-1}f''(\xi_k)\le n\cdot\textit{fmax}$，则 $\textit{fmin}\le\sum_{k=0}^{n-1}\frac{f''(\xi_k)}{n}\le\textit{fmax}$。

又由介值定理得，必定存在 $\eta\in[a,b]$ 使 $\sum_{k=0}^{n-1}\frac{f''(\xi_k)}{n}=f''(\eta)$，我们再令 $h=\frac{b-a}{n}$（即步长），得到

$$\int^b_a f(x)\mathrm{d}x-(2)=-\frac{(b-a)^2}{n^2}\cdot(b-a)\cdot\frac{1}{12}\sum_{k=0}^{n-1}\frac{f''(\xi_k)}{n}=-\frac{h^2}{12}(b-a)f''(\eta)\kern{25px}(9)$$

即复化梯形求积公式的余项公式为 $-\frac{h^2}{12}(b-a)f''(\eta)$，其中 $\eta$（根据定义）与步长 $h$ 正相关（即不含 $h$ 的负数次项）。

到重头戏了。

为了能够对复化梯形求积公式（即 $(2)$，下称 $F(h)$，$h$ 为步长）使用理查德森外推法，我们将复化梯形求积公式的余项公式写成幂级数的形式。

由于 $\eta$ 与步长 $h$ 正相关，我们有，

$$\int^b_a f(x)\mathrm{d}x-(2)=-\frac{h^2}{12}(b-a)f''(\eta)=\sum_{k=1}^\infty\alpha_kh^{2k}\kern{25px}(10)$$

即 $(3)(4)$ 中的 $p=2,q=4$。

我们令 $(3)$ 中的 $h$ 等于 $(4)$ 中 $h_2$ 的 $\frac{1}{2}$，则由 $(5)$ 与 $(10)$ 得

$\Large F^*(h_2)=\frac{F(h)-\left({\frac {h}{h_{2}}}\right)^{p}F(h_{2})}{1-\left({\frac {h}{h_{2}}}\right)^{p}}=\frac{F(\frac{h_2}{2})-\frac{1}{4}F(h_2)}{1-\frac{1}{4}}=\frac{4F(\frac{h_2}{2})-F(h_2)}{3}$

此时误差来到 $\sum_{k=2}^\infty\alpha_kh^{2k}$，即 $p=4,q=6$。

下一个更精确的函数则是

$\Large F^{**}(h_2)=\frac{F^*(h)-\left({\frac {h}{h_{2}}}\right)^{p}F^*(h_{2})}{1-\left({\frac {h}{h_{2}}}\right)^{p}}=\frac{F^*(\frac{h_2}{2})-\frac{1}{16}F^*(h_2)}{1-\frac{1}{16}}=\frac{16F^*(\frac{h_2}{2})-F^*(h_2)}{15}$

以此不断使用理查德森外推法，我们可以定义龙贝格函数 $R(n,m)$：

$$R(n,m)=\Large\left\{\begin{matrix} \frac{(f(a)+f(b))(b-a)}{2}&(n=m=0)&\text{\small注：梯形公式}\\ \frac{R(n-1,0)}{2}+\frac{b-a}{2^n}\sum\limits_{k=1}^{2^{n-1}}f(a+\frac{(b-a)(2k-1)}{2^n})&(n\not=0,m=0)&\text{\small注：复化梯形求积公式，步长为}{\small\frac{1}{2^n}}\\ \frac{4^mR(n,m-1)-R(n-1,m-1)}{4^m-1}&otherwise&\text{\small注：上面的理查德森外推法} \end{matrix}\right.$$

而由定义可以得到以下式子：

$$\int_a^bf(x)\mathrm{d}x=\lim_{n,m\rightarrow\infty}R(n,m)$$

于是我们递推处理龙贝格函数，直到达到精度要求即可。

贴一张图以助于理解：

$$\tiny\color{grey}\text{图~3，龙贝格函数表的计算，摘自@sola}$$

最好写、最不容易写错、但不是最快速的一种。

根据龙贝格函数直接搞。

注：为了避免空间占用过大所以没有使用二维数组。

题面是一个反常积分，那显然把 $b$ 开足够大即可，发散当且仅当 $a>a; if(a>T; for(int i=1;i>D>>H>>B>>L,l=0,r=H,n=(B-1)/D+1,L/=n,W=B/n; while(l+1e-9l