| 关于虚数与复数 | 您所在的位置：网站首页 › python提取复数的实部和虚部 › 关于虚数与复数 |
关于虚数与复数
|
关于虚数与复数
1 数的分类1.1 实数域1.2 虚数与复数
2 复数的性质及其运算2.1 复平面、大小及辐角2.2 复数四则运算2.3 共轭复数2.4 复数的极坐标表示
3 欧拉公式3.1 欧拉公式证明3.2 利用欧拉公式表示极坐标3.3 欧拉公式推导三角函数加法定理
4 复数的性质、乘法和除法运算和极坐标表示方法4.1 复数乘法4.1.1 直角坐标系中计算4.1.2 极坐标下计算
4.1 复数除法
参考
实数按照大小排列可以构成实数轴，复数不属于实数，所以复数并不在实数轴上。实数轴添加一个虚数轴构成复平面，复数可以表示为复平面上的一个点。复数有大小和辐角，复平面上的点利用大小和辐角表示就是极坐标。极坐标可以通过三角函数转为复平面直角坐标
a
+
b
i
=
r
c
o
s
θ
+
i
r
s
i
n
θ
=
r
(
c
o
s
θ
+
i
s
i
n
θ
)
a + bi=rcos\theta+irsin\theta=r(cos\theta+isin\theta)
a+bi=rcosθ+irsinθ=r(cosθ+isinθ)。通过引入欧拉公式
e
i
θ
=
c
o
s
θ
+
i
s
i
n
θ
e^{iθ}=cosθ+isinθ
eiθ=cosθ+isinθ，它能通过复指数表示复数(三角函数形式)，复指数中系数表示大小，θ 为辐角。通过复指数能够大大简化运算。函数的相互转化:
a
+
b
i
=
r
c
o
s
θ
+
i
r
s
i
n
θ
=
r
(
c
o
s
θ
+
i
s
i
n
θ
)
=
r
e
i
θ
a + bi=rcos\theta+irsin\theta=r(cos\theta+isin\theta)=re^{iθ}
a+bi=rcosθ+irsinθ=r(cosθ+isinθ)=reiθ
1 数的分类
1.1 实数域
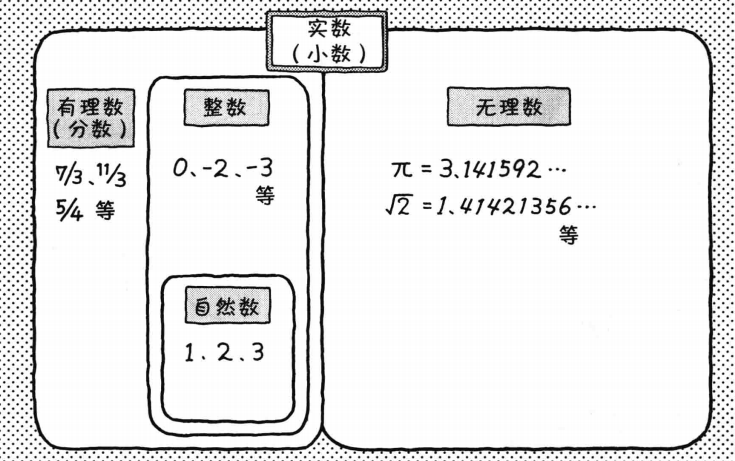
自然数：最常用的数为自然数，有些人指正整数，有些人则指非负整数。前者多在数论中被使用，而在集合论和计算机科学中则多使用后者的定义。如：1、2、3… 整数 = 负数 + 0 + 自然数 有理数：有理数是指可以被表示成整数分子(m)和非零整数分母(n)的分数的数，即 m / n m/n m/n，其代表 1 被分做相同的 n 份，再取 m 份后的量。分数可以是正的、负的、或零。所有分数所组成的集合包含有整数，因为每一个整数都可以写成分母为 1 的分数。有理数的符号为ℚ 无理数：无限不循环小数 实数 = 有理数 + 无理数，实数的符号为 R 。 下图是数的包含关系 虚数：虚数
i
i
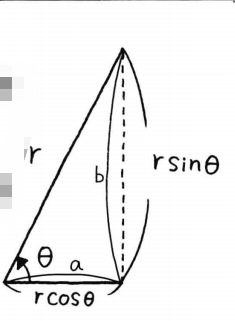
i，英文 imaginary number，表示由想象力创造出来的数。 复数： 实数 + 虚数 的形式 a + b i a + bi a+bi，其中 a 和 b 是实数，分别表示复数的“实部”和“虚部”。 2 复数的性质及其运算现有复数： 3 + 2 i 3 + 2i 3+2i 2.1 复平面、大小及辐角复平面：以实部为横轴即实数轴，以虚部为纵轴即虚数轴，复数就是这个平面上的点 实部之间，虚部之间可以进行四则运算。 共轭复数，与原复数虚部正负号相反的复数称为共轭复数 在数学中，极坐标系（英语：Polar coordinate system）是一个二维坐标系统。该坐标系统中任意位置可由一个夹角和一段相对原点—极点的距离来表示。 对于一个复数我们可以计算其大小和辐角，所以可以用极坐标系表示。如复数
4
+
3
i
4+3i
4+3i，其大小为 r = 5，辐角为
θ
=
a
r
c
t
a
n
(
3
/
4
)
\theta=arctan(3/4)
θ=arctan(3/4)， 极坐标就是
(
5
,
a
r
c
t
a
n
(
3
/
4
)
(5, arctan(3/4)
(5,arctan(3/4) 当我们有极坐标 ( r , θ ) (r, \theta) (r,θ) ,就可以利用三角函数将极坐标转换到直角坐标。 上图中三角形抽离出来： a = r cos θ , b = r sin θ a = r \cos\theta, b = r \sin\theta a=rcosθ,b=rsinθ。即 复 数 = 实 部 + 虚 部 = a + b i = r cos θ + i r sin θ 复数 =实部 + 虚部 =a+bi= r \cos\theta + ir \sin\theta 复数=实部+虚部=a+bi=rcosθ+irsinθ 综上，所以表示复平面上点的方法有两种，一种是用直角坐标系来表示，另一种是用极坐标系来表示。要根据目的选择便于使用的坐标系、 3 欧拉公式欧拉公式一般表现形式： e i θ = c o s θ + i s i n θ e^{iθ}=cosθ+isinθ eiθ=cosθ+isinθ 当 θ = π θ=π θ=π 时，有 e i π + 1 = 0 e^{iπ}+1=0 eiπ+1=0 纳皮尔常数 e 定义: 复指数
e
i
x
e^ix
eix 麦克劳伦展开: 附:棣(di 四声)莫弗公式 2.4 节利用极坐标表示复数： 复 数 = 实 部 + 虚 部 = a + b i = r cos θ + i r sin θ 复数 =实部 + 虚部 = a + bi = r \cos\theta + ir \sin\theta 复数=实部+虚部=a+bi=rcosθ+irsinθ 其中 r = a 2 + b 2 r =\sqrt{a^2 + b^2} r=a2+b2 ， 辐角 θ = a r c t a n ( b / a ) \theta=arctan(b/a) θ=arctan(b/a) 利用欧拉公式有： r cos θ + i r sin θ = r ( cos θ + i sin θ ) = r e i θ r \cos\theta + ir \sin\theta=r(\cos\theta+i\sin\theta)=re^{i\theta} rcosθ+irsinθ=r(cosθ+isinθ)=reiθ 3.3 欧拉公式推导三角函数加法定理三角函数加法定理，根据欧拉公式 e i θ = c o s θ + i s i n θ e^{iθ}=cosθ+isinθ eiθ=cosθ+isinθ有： e i ( α + β ) = c o s ( α + β ) + i s i n ( α + β ) e^{i(α+β)}=cos(α+β)+isin(α+β) ei(α+β)=cos(α+β)+isin(α+β) 根据指数计算规则又有： e i ( α + β ) = e i α ∗ e i β = ( c o s α + i s i n α ) ∗ ( c o s β + i s i n β ) = c o s α c o s β − s i n α s i n β + i ( c o s α s i n β + s i n α c o s β ) e^{i(α+β)}=e^{iα}*e^{iβ}=(cosα+isinα)*(cosβ+isinβ)=cosαcosβ-sinαsinβ+i(cosαsinβ+sinαcosβ) ei(α+β)=eiα∗eiβ=(cosα+isinα)∗(cosβ+isinβ)=cosαcosβ−sinαsinβ+i(cosαsinβ+sinαcosβ) 上面两式中实部和虚部对应相等，所以有： 现在假设我们有两个复数 1 + 2 i 1+2i 1+2i 和 3 + 4 i 3+4i 3+4i 4.1.1 直角坐标系中计算计算两个复数的乘积，在直角坐标系中的乘法计算： 极坐标下的两个复数，使用欧拉公式表示有： 复数 1 + 2 i 1+2i 1+2i 和 3 + 4 i 3+4i 3+4i，计算极坐标，极坐标分别为 ( 5 \sqrt{5} 5 , 1.1 r a d 1.1rad 1.1rad)={ r 1 = 1 + 2 2 = 5 , θ 1 = a r c t a n ( 2 / 1 ) = 1.1 弧 度 r_1=\sqrt{1+2^2}=\sqrt{5},\theta_1=arctan(2/1)=1.1弧度 r1=1+22 =5 ,θ1=arctan(2/1)=1.1弧度} 和 ( 5 5 5, 0.93 r a d 0.93rad 0.93rad)={ r 2 = 3 2 + 4 2 = 5 , θ 2 = a r c t a n ( 4 / 3 ) = 0.93 弧 度 r_2=\sqrt{3^2+4^2}=5,\theta_2=arctan(4/3)=0.93弧度 r2=32+42 =5,θ2=arctan(4/3)=0.93弧度} 利用欧拉公式将极坐标转为复指数： 5 e i 1.1 ∗ 5 e i 0.93 = 5 5 e i 1.1 + 0.93 = 5 5 e i 2.03 \sqrt{5}e^{i1.1}*5e^{i0.93}=5\sqrt{5}e^{i1.1+0.93}=5\sqrt{5}e^{i2.03} 5 ei1.1∗5ei0.93=55 ei1.1+0.93=55 ei2.03 2.03 弧度约等于 116.6 度，可见利用极坐标我们能很快算出乘积结果。 复数的乘法运算表示旋转，如下图，
(
1
+
2
i
)
∗
(
3
+
4
i
)
(1+2i)*(3+4i)
(1+2i)∗(3+4i),相当于
3
+
4
i
3+4i
3+4i 先将大小放大(或缩小)
r
1
=
1
+
2
2
=
5
r_1=\sqrt{1+2^2}=\sqrt{5}
r1=1+22
=5
倍，随后旋转
a
r
c
t
a
n
(
2
/
1
)
arctan(2/1)
arctan(2/1)弧度 分母有理化计算除法 数 复数 (数学) 漫画虚数和复数 复数的几种表示形式 |
所有实数按大小顺序排列后的形成的就是数轴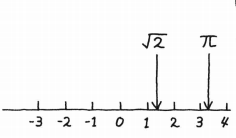 
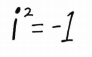因为虚数不是实数，所以不在数轴上
复数大小计算公式：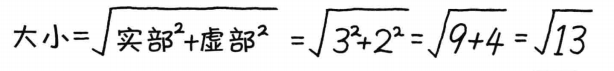 
辐角计算：
θ
=
a
r
c
t
a
n
(
虛
部
/
实
部
)
=
a
r
c
t
a
n
(
b
/
a
)
=
a
r
c
t
a
n
(
2
/
3
)
=
0.588
弧
度
θ = arctan(虛部/实部)=arctan(b/a)=arctan(2/3)=0.588 弧度
θ=arctan(虛部/实部)=arctan(b/a)=arctan(2/3)=0.588弧度 附：关于弧度定义可参考数字信号处理-2-三角函数与谱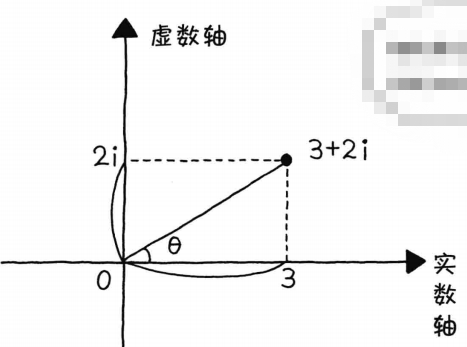 
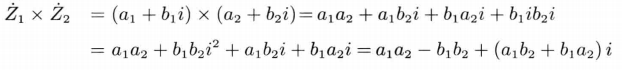
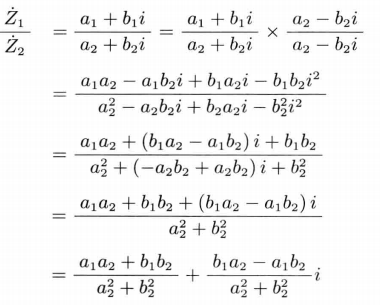
复数与它的共轭复数大小相同，但是辐角的正负号相反 
复数与它的共轭复数之间相加、相乘、相除都会得到实数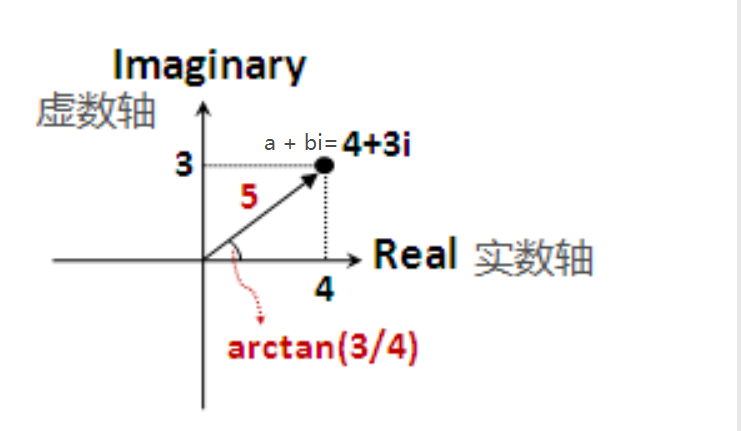
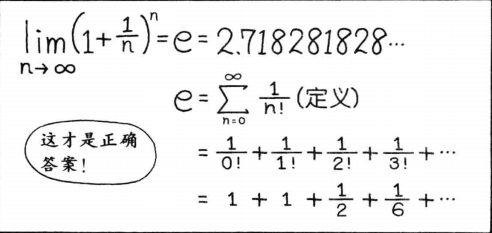
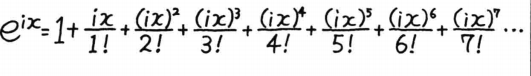根据
i
2
=
−
1
i^2=-1
i2=−1 有：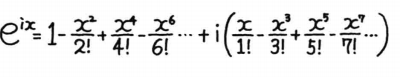 
c
o
s
x
cosx
cosx 与
s
i
n
x
sinx
sinx 的麦克劳伦展开 
三角函数替换复指数中右侧，得到欧拉公式：
e
i
x
=
c
o
s
x
+
i
s
i
n
x
e^{ix}=cosx+isinx
eix=cosx+isinx
棣莫弗公式由欧拉公式推出：
(
e
i
x
)
n
=
e
i
x
n
=
(
e
n
x
)
i
=
c
o
s
(
n
x
)
+
i
s
i
n
(
n
x
)
(e^{ix})^n=e^{ixn}=(e^{nx})^i=cos(nx)+isin(nx)
(eix)n=eixn=(enx)i=cos(nx)+isin(nx)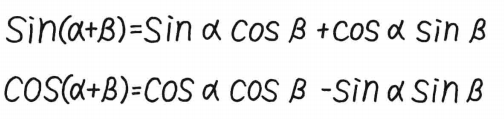
也即三角函数的加法定理。
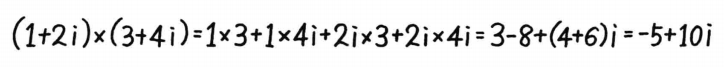可见计算麻烦，现在将结果
−
5
+
10
i
-5+10i
−5+10i 用极坐标(需要计算大小和辐角)表示：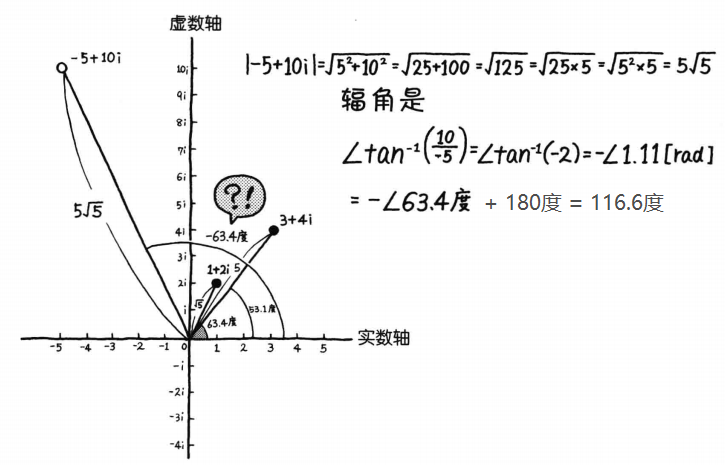 
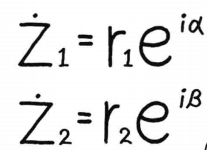进行乘法运算有： 
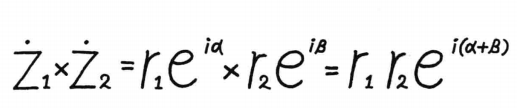复指数乘法将两个复数的大小相乘，辐角相加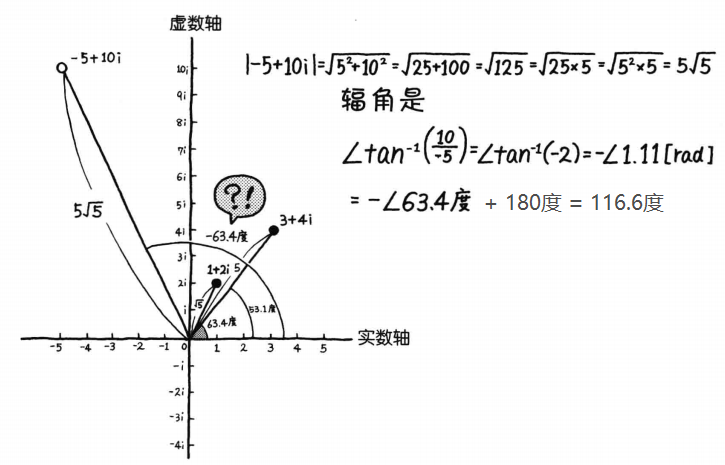
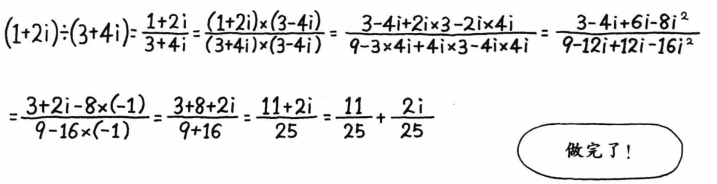极坐标方式计算除法，也即把大小和辐角分别进行除法运算： 
欧拉公式表示除法：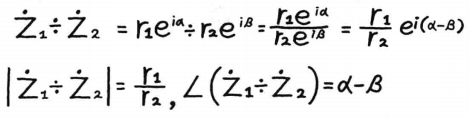 
5
e
i
1.1
÷
5
e
i
0.93
=
(
5
/
5
)
∗
e
i
1.1
−
0.93
=
(
5
/
5
)
e
i
0.18
\sqrt{5}e^{i1.1}÷5e^{i0.93}=(5/\sqrt{5})*e^{i1.1-0.93}=(\sqrt{5}/5)e^{i0.18}
5
ei1.1÷5ei0.93=(5/5
)∗ei1.1−0.93=(5
/5)ei0.18【本文地址】