| 2.8: 求解绝对值不等式 | 您所在的位置:网站首页 › log不等式求解 › 2.8: 求解绝对值不等式 |
2.8: 求解绝对值不等式
|
学习目标
在本节结束时,您将能够: 求解绝对值方程 用 “小于” 求解绝对值不等式 用 “大于” 求解绝对值不等式 用绝对值求解应用程序在开始之前,请参加这个准备测验。 评估:\(−|7|\)。 如果你错过了这个问题,请查看 [链接]。 \(=\)为以下每对数字填写\(,,\)或。 ⓐ\(|−8|\text{___}−|−8|\) ⓑ\(12\text{___}−|−12|\) ⓒ\(|−6|\text{___}−6\) ⓓ\(−(−15)\text{___}−|−15|\) 如果你错过了这个问题,请查看 [链接]。 简化:\(14−2|8−3(4−1)|\)。 如果你错过了这个问题,请查看 [链接]。 求解绝对值方程在我们准备求解绝对值方程时,我们会回顾我们对绝对值的定义。 绝对值数字的绝对值是它在数字线上与零的距离。 数字 n 的绝对值写成所有数字\(|n|\)的\(|n|\geq 0\) and。 绝对值始终大于或等于零。 我们了解到,在数字线上,数字及其对数与零的距离是相同的。 由于它们与零的距离相同,因此它们的绝对值相同。 例如: \(−5\)距离 0 有 5 个单位的距离,所以\(|−5|=5\)。 \(5\)距离 0 有 5 个单位的距离,所以\(|5|=5\)。该图\(\PageIndex{1}\)说明了这个想法。 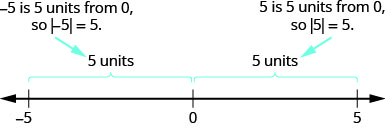 图\(\PageIndex{1}\):数字 5 和 5\(−5\) 均距离零五个单位。
图\(\PageIndex{1}\):数字 5 和 5\(−5\) 均距离零五个单位。
对于方程 |x|=5, |x|=5,我们正在寻找所有能使其成为真实陈述的数字。 我们正在寻找与零的距离为 5 的数字。 我们刚刚看到 5 和 −5−5 在数字行上都是从零开始的五个单位。 它们是方程的解。 \(\begin{array} {ll} {\text{If}} &{|x|=5} \\ {\text{then}} &{x=−5\text{ or }x=5} \\ \end{array}\) 通过写作,可以将解决方案简化为单个语句\(x=\pm 5\)。 读作 “x 等于正或负 5”。 我们可以将其概括为绝对值方程的以下属性。 绝对值方程对于任何代数表达式 u 和任何正实数 a \[\begin{array} {ll} {\text{if}} &{|u|=a} \\ {\text{then}} &{u=−a \text{ or }u=a} \\ \nonumber \end{array}\] 请记住,绝对值不能是负数。 示例\(\PageIndex{1}\)解决: \(|x|=8\) \(|y|=−6\) \(|z|=0\) 解决方案 a\(\begin{array} {ll} {} &{|x|=8} \\ {\text{Write the equivalent equations.}} &{x=−8 \text{ or } x=8} \\ {} &{x=\pm 8} \\ \end{array}\) 解决方案 b\(\begin{array} {ll} {} &{|y|=−6} \\ {} &{\text{No solution}} \\ \end{array}\) 由于绝对值始终为正,因此该方程没有解。 解决方案 c\(\begin{array} {ll} {} &{|z|=0} \\ {\text{Write the equivalent equations.}} &{z=−0\text{ or }z=0} \\ {\text{Since }−0=0,} &{z=0} \\ \end{array}\) 两个方程都告诉我们 z=0z=0 所以只有一个解。 锻炼\(\PageIndex{2}\)解决: \(|x|=2\) \(|y|=−4\) \(|z|=0\) 回答 a\(\pm 2\) 答案 b没有解决办法 答案 c0 锻炼\(\PageIndex{3}\)解决: \(|x|=11\) \(|y|=−5\) \(|z|=0\) 回答 a\(\pm 11\) 答案 b没有解决办法 答案 c0 为了求解绝对值方程,我们首先使用与求解线性方程相同的程序隔离绝对值表达式。 隔离绝对值表达式后,我们将其重写为两个等效方程。 如何求解绝对值方程 示例\(\PageIndex{4}\)解决\(|5x−4|−3=8\)。 解决方案
解决:\(|3x−5|−1=6\)。 回答\(x=4, \space x=−\frac{2}{3}\) 锻炼\(\PageIndex{6}\)解决:\(|4x−3|−5=2\)。 回答\(x=−1,\space x=\frac{5}{2}\) 这里总结了求解绝对值方程的步骤。 求解绝对值方程。 隔离绝对值表达式。 写出等效方程式。 求解每个方程。 检查每种解决方案。 示例\(\PageIndex{7}\)解决\(2|x−7|+5=9\). 解决方案 \(2|x−7|+5=9\) 隔离绝对值表达式。 \(2|x−7|=4\) \(|x−7|=2\) 写出等效方程式。 \(x−7=−2\)或\(x−7=2\) 求解每个方程。 \(x=5\)或\(x=9\) 查看: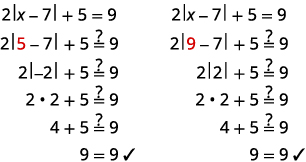 练习\(\PageIndex{8}\)
练习\(\PageIndex{8}\)
解决:\(3|x−4|−4=8\)。 回答\(x=8,\space x=0\) 练习\(\PageIndex{9}\)解决:\(2|x−5|+3=9\)。 回答\(x=8,\space x=2\) 记住,绝对值总是正数! 示例\(\PageIndex{10}\)解决:\(|\frac{2}{3}x−4|+11=3\)。 解决方案\(\begin{array} {ll} {} &{|\frac{2}{3}x−4|=−8} \\ {\text{Isolate the absolute value term.}} &{|\frac{2}{3}x−4|=−8} \\ {\text{An absolute value cannot be negative.}} &{\text{No solution}} \\ \end{array}\) 练习\(\PageIndex{11}\)解决:\(|\frac{3}{4}x−5|+9=4\)。 回答没有解决办法 练习\(\PageIndex{12}\)解决:\(|\frac{5}{6}x+3|+8=6\)。 回答没有解决办法 我们的一些绝对值方程可能采用其\(|u|=|v|\)中 u 和 v 是代数表达式的形式。 例如,\(|x−3|=|2x+1|\)。 我们将如何解决这些问题? 如果两个代数表达式的绝对值相等,则它们要么彼此相等,要么彼此为负数。 绝对值方程的属性表示,对于任何代数表达式 u 和正实数,a、if\(|u|=a\)、then\(u=−a\) 或\(u=a\)。 这告诉我们了 \ (\ begin {array} {lll} {\ text {if}} & {|u|=|v|} & {}\\ {\ text {then}} & {|u|=v} & {|u|=−v} \\ {\ text {and so}} & {u=v\ text {or} u = −v} & {\ text {or}} & {u=−v\ text {or} u = − (−v)} \\\ end {array}\) 这使我们得出具有两个绝对值的方程的以下属性。 具有两个绝对值的方程对于任何代数表达式 u 和 v, \[\begin{array} {ll} {\text{if}} &{|u|=|v|} \\ {\text{then}} &{u=−v\text{ or }u=v} \\ \nonumber \end{array}\] 当我们取与数量相反的值时,我们必须谨慎对待符号,并在需要时添加圆括号。 示例\(\PageIndex{13}\)解决:\(|5x−1|=|2x+3|\)。 解决方案\(\begin{array} {ll} {} &{} &{|5x−1|=|2x+3|} &{} \\ {} &{} &{} &{} \\ {\text{Write the equivalent equations.}} &{5x−1=−(2x+3)} &{\text{or}} &{5x−1=2x+3} \\ {} &{5x−1=−2x−3} &{\text{or}} &{3x−1=3} \\ {\text{Solve each equation.}} &{7x−1=−3} &{} &{3x=4} \\ {} &{7x=−2} &{} &{x=43} \\ {} &{x=−27} &{\text{or}} &{x=43} \\ {\text{Check.}} &{} &{} &{} \\ {\text{We leave the check to you.}} &{} &{} &{} \\ \end{array}\) 练习\(\PageIndex{14}\)解决:\(|7x−3|=|3x+7|\)。 回答\(x=−\frac{2}{5}, \space x=\frac{5}{2}\) 练习\(\PageIndex{15}\)解决:\(|6x−5|=|3x+4|\)。 回答\(x=3, x=19\) 用 “小于” 求解绝对值不等式现在让我们来看看当我们存在绝对值不等式时会发生什么。 我们所学到的关于解决不平等的一切仍然有效,但我们必须考虑绝对价值如何影响我们的工作。 再说一遍,我们将看看我们对绝对值的定义。 数字的绝对值是它在数字线上与零的距离。 对于方程\(|x|=5\),我们看到数字线上\(−5\)的 5 和 5 都是 0 的五个单位。 它们是方程的解。 \[\begin{array} {lll} {} &{|x|=5} &{} \\ {x=−5} &{\text{or}} &{x=5} \\ \nonumber \end{array}\] 那不平等\(|x|\leq 5\)呢? 距离小于或等于 5 的数字在哪里? 我们知道\(−5\)和 5 都是从零开始的五个单位。 \(−5\)和 5 之间的所有数字从零开始小于五个单位(图\(\PageIndex{2}\))。 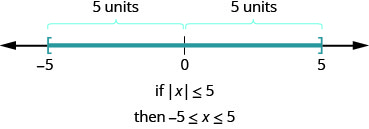 图\(\PageIndex{2}\)。
图\(\PageIndex{2}\)。
用更一般的方式,我们可以看出 if\(|u|\leq a\),那么\(−a\leq u\leq a\)(图\(\PageIndex{3}\))。 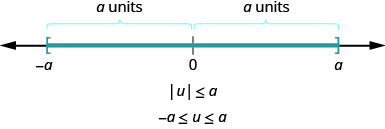 图\(\PageIndex{3}\)。
图\(\PageIndex{3}\)。
此处总结了此结果。 绝对值不等式\( |
【本文地址】



