运筹优化求解迭代过程案例:图解法、单纯形法、单纯形表

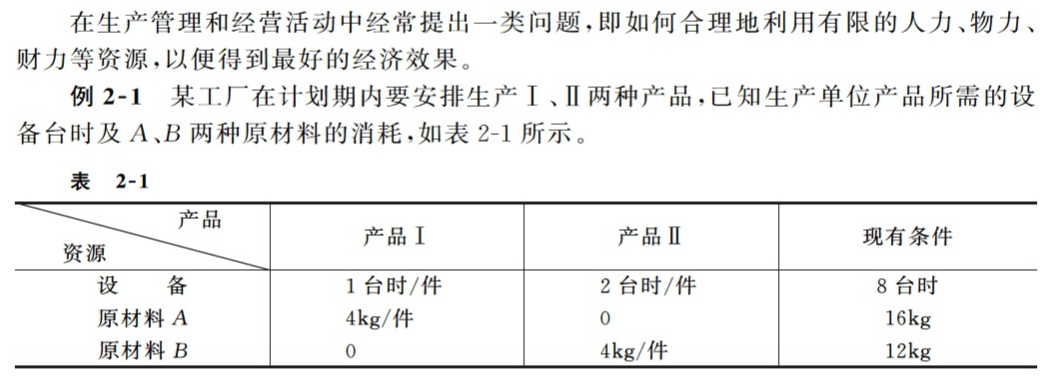
题目来自于清华大学出版的《运筹学》第四版。

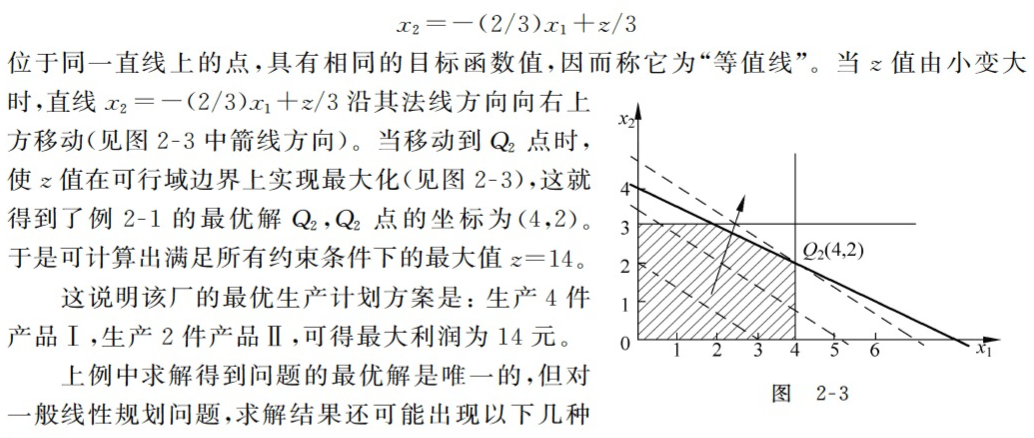
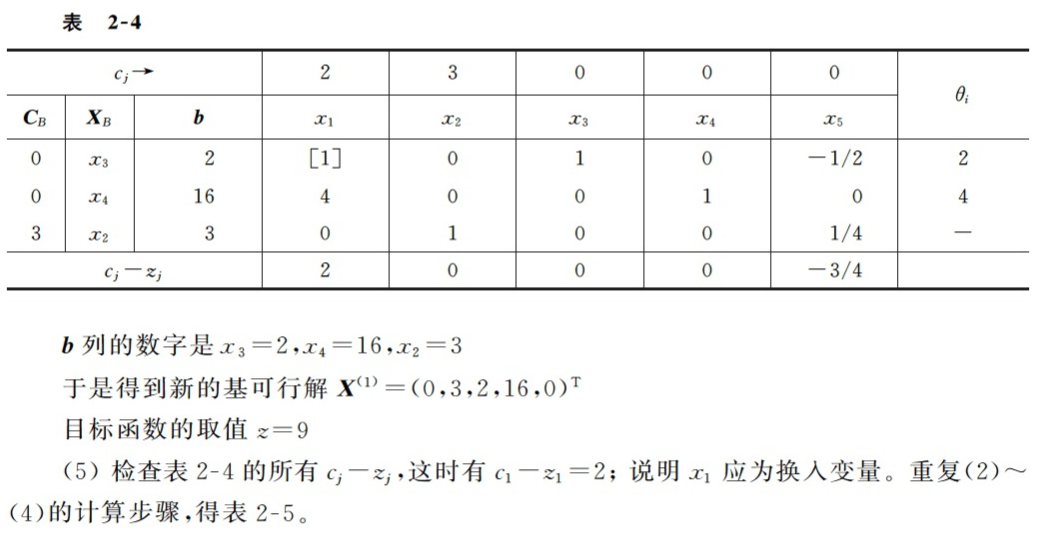
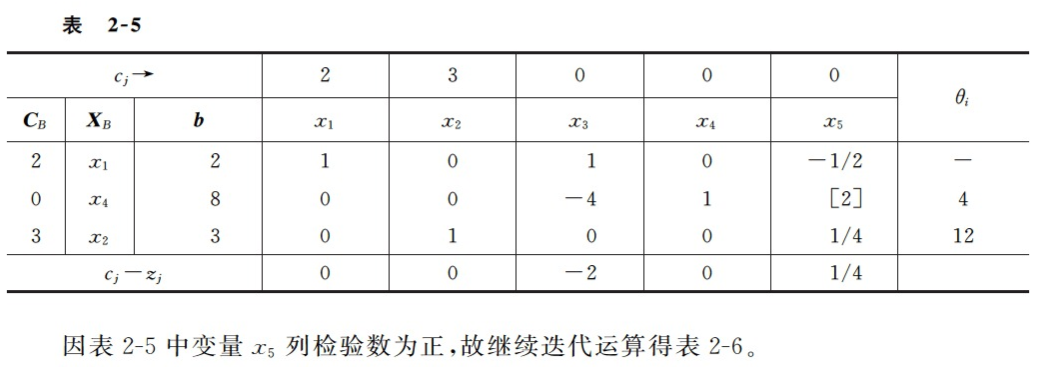
下面描述一下第三次迭代的详细过程：

从表达式（2-18）可以看到，决策变量x1系数为正，如果生产x1，则目标函数值会大于9，因此非基变量x1要进基。那么x2、x3、x4哪个出基呢？

表达式（2-17）中有x1的是第一个和第二个等式; 从第一个等式可以看出，由于x3要>=0，x5不会进基依然是非基变量，所以x5=0，这时x1最大可以为2/1=2；从第二个等式可以看出，由于x4要>=0，这时x1最大可以为16/4=4；因此x1会先达到第一个等式的约束，所以第一个等式中的x1进基(移动到等式的左边)，而x3要出基（移动到等式的右边）。表达式（2-17）的等式一修改后得到： { x 1 = 2 − x 3 + 1 2 x 5 x 4 = 16 − 4 x 1 x 2 = 3 − 1 4 x 5 \begin{equation} \left\{ \begin{array}{lr} x_1 = 2 - x_3 + \frac{1}{2}x_5 & \\ x_4 = 16 - 4x_1 & \\ x_2 = 3 -\frac{1}{4}x_5 & \end{array} \right. \end{equation} ⎩ ⎨ ⎧​x1​=2−x3​+21​x5​x4​=16−4x1​x2​=3−41​x5​​​​​ 表达式（2-17）的等式二修改后得到新的基变量(x1,x2,x4)： { x 1 = 2 − x 3 + 1 2 x 5 x 4 = 8 + 4 x 3 − 2 x 5 ( 2 − 18 − 1 ) x 2 = 3 − 1 4 x 5 \begin{equation} \left\{ \begin{array}{lr} x_1 = 2 - x_3 + \frac{1}{2}x_5 & \\ x_4 = 8 + 4x_3 - 2x_5 &&&&&&&&&&&&&&&& (2-18-1)\\ x_2 = 3 -\frac{1}{4}x_5 & \end{array} \right. \end{equation} ⎩ ⎨ ⎧​x1​=2−x3​+21​x5​x4​=8+4x3​−2x5​x2​=3−41​x5​​​​​​​​​​​​​​​​​(2−18−1)​​​ 带入到目标函数得到： z = 13 − 2 x 3 + 1 4 x 5                                            ( 2 − 18 − 2 ) z = 13 - 2x_3 + \frac{1}{4}x_5 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2-18-2) z=13−2x3​+41​x5​                                          (2−18−2) 让非基变量x3=x5=0，得到大目标函数最大值13，基可行解是（2，3，0，8，0）。

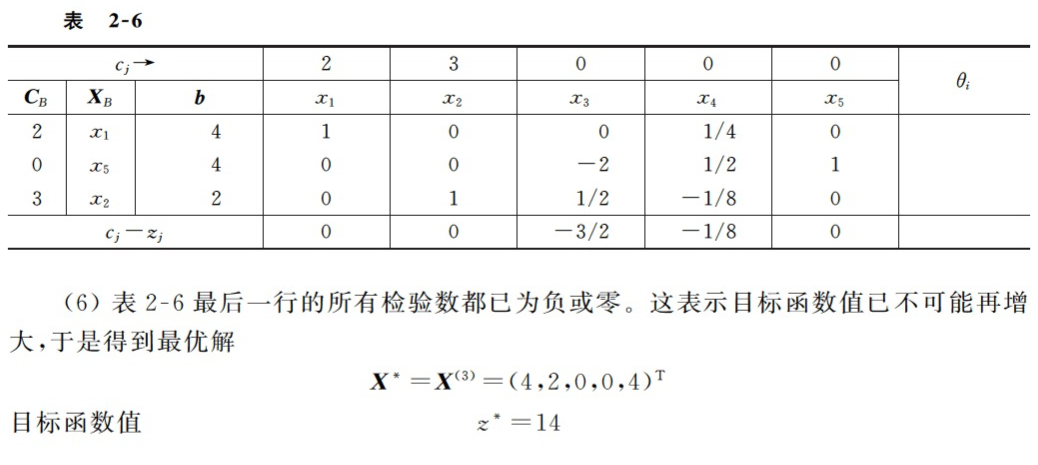
下面描述一下第四次迭代的详细过程：

从第三次迭代得到的目标函数（2-18-2）可以看出，x5的系数是1/4>0，说明生产x5后，目标函数值还会变大，所以x5要进基，那x1、x2、x4哪个会出基呢？

表达式（2-18-1）中的三个等式都有x5。从第一个等式可以看出，x1要>=0，x5>=-4，-4已经小于0就不考虑了；从第二个等式可以看出，x4>=0，x5的最大值是8/2=4；从第三个等式可以看出，x2>=0，x5的最大值是3/(1/4)=12；要从x5的值（-4,4,12）中，选择正数中最小的那个，也就是4，所以（2-18-1）中的第二个等式中的x5要进基(移动到等号左边)，x4要出基(移动到等号的右边)，得到： { x 1 = 2 − x 3 + 1 2 x 5 x 5 = 4 + 2 x 3 − 1 2 x 4 x 2 = 3 − 1 4 x 5 \begin{equation} \left\{ \begin{array}{lr} x_1 = 2 - x_3 + \frac{1}{2}x_5 & \\ x_5 = 4 + 2x_3 - \frac{1}{2}x_4 \\ x_2 = 3 -\frac{1}{4}x_5 & \end{array} \right. \end{equation} ⎩ ⎨ ⎧​x1​=2−x3​+21​x5​x5​=4+2x3​−21​x4​x2​=3−41​x5​​​​​ 在将上面的第一个和第三个等式中的x5用第二个等式替换，后得到新的基变量(x1,x2,x5)： { x 1 = 4 − 1 4 x 4 x 5 = 4 + 2 x 3 − 1 2 x 4 x 2 = 2 − 1 2 x 3 + 1 8 x 4 \begin{equation} \left\{ \begin{array}{lr} x_1 = 4 - \frac{1}{4}x_4 & \\ x_5 = 4 + 2x_3 - \frac{1}{2}x_4 \\ x_2 = 2 -\frac{1}{2}x_3 + \frac{1}{8}x_4 & \end{array} \right. \end{equation} ⎩ ⎨ ⎧​x1​=4−41​x4​x5​=4+2x3​−21​x4​x2​=2−21​x3​+81​x4​​​​​ 带入到目标函数得到： z = 14 − 3 2 x 3 − 1 8 x 4 z = 14 - \frac{3}{2}x_3 - \frac{1}{8}x_4 z=14−23​x3​−81​x4​ 让非基变量x3=x4=0，得到大目标函数最大值14，基可行解是（4，2，0，0，4）。

因为上述目标函数中x3和x4的系数都小于0了，x3和x4都要>=0，所以目标函数不会再变大了，最大就是14。

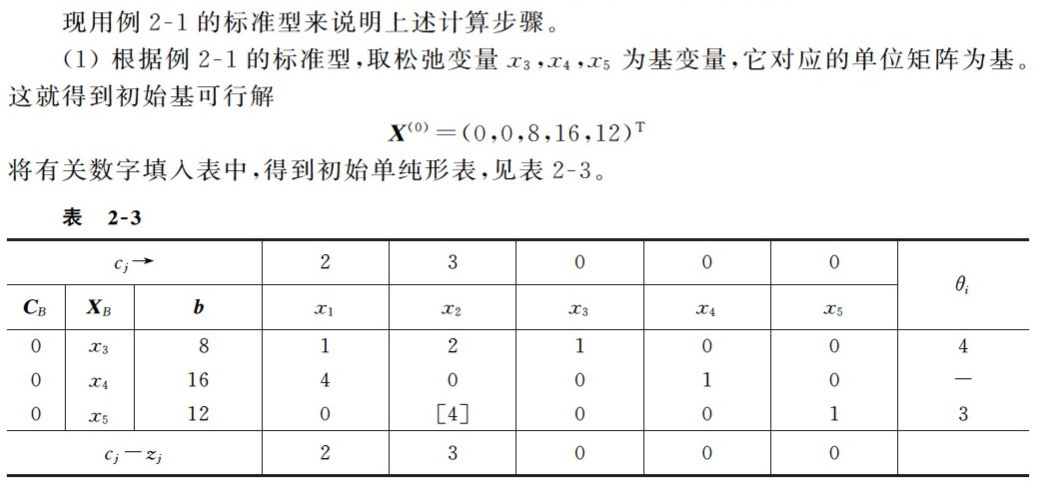
这里可以看到，初始基是原点，迭代的过程就是从原点开始，找到可行域的下一个顶点验证的过程。