第六节、双目视觉之相机标定

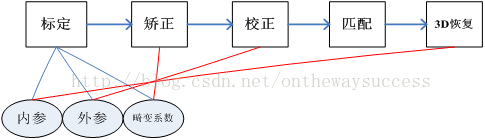
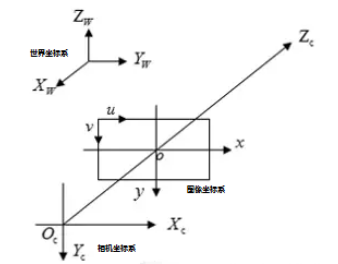
去年三四月份实验室做了一个机器人与视觉识别系统的项目，主要就是利用双目摄像头进行物体空间坐标定位，然后利用机器人进行抓取物体。当时我才研一，还是个菜鸡，项目主要是几个学长负责做的，我也就是参与打打酱油，混混经验。现在过了一年多了，机器人一直在实验室放着，空着也是浪费，所以就想搞点事情。这里我们就先从利用双目摄像头进行空间定位说起，因为这是整个项目的核心部分。

双目视觉是建立在几何数学的基础上，数学推导是枯燥乏味的。因此这里不去过多的介绍数学原理，只是简要的叙述一下双目视觉的流程。

双目视觉主要包括相机标定、图片畸变矫正、摄像机校正、图片匹配、3D恢复五个部分。

下面我们从相机标定开始说起。相机标定的目的有两个。

谈到相机标定，我们不得不说起摄相机坐标系、世界坐标系、图像坐标系。

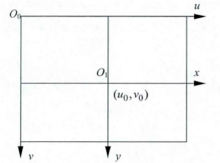
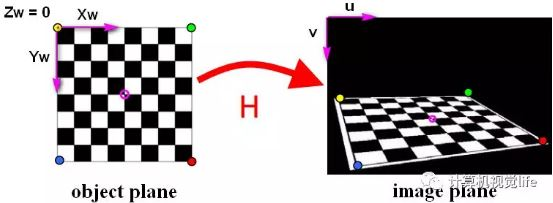
上图是三个坐标的示意简图，通过它大家可以对三个坐标有一个直观的认识。

备注：有很多人把图像坐标系和像素坐标系合在一起，称作三大坐标系，也有人分开，称为四大坐标系。

讲到这里，你可能会问有了图像坐标系为什么还要建一个像素坐标系？

我们以图像左上角为原点建立以像素为单位的直接坐标系$u$-$v$。像素的横坐标$u$与纵坐标$v$分别是在其图像数组中所在的列数与所在行数。

由于$(u,v)$只代表像素的列数与行数，而像素在图像中的位置并没有用物理单位表示出来，所以，我们还要建立以物理单位（如毫米）表示的图像坐标系$x$-$y$。

将相机光轴与图像平面的交点（一般位于图像平面的中心处，也称为图像的主点（principal point）定义为该坐标系的原点$O_1$，且$x$轴与$u$轴平行，$y$轴与$v$轴平行，假设$(u_0,v_0)$代表$O_1$在$u$-$v$坐标系下的坐标，$dx$与$dy$分别表示每个像素在横轴$x$和纵轴$y$上的物理尺寸，则图像中的每个像素在$u$-$v$坐标系中的坐标和在$x$-$y$坐标系中的坐标之间都存在如下的关系：

$$u=\frac{x}{dx}+u_0$$

$$v=\frac{y}{dy}+v_0$$

其中，我们假设物理坐标系中的单位为毫米，那么$dx$的的单位为:毫米/像素。那么$x/dx$的单位就是像素了，即和$u$的单位一样都是像素。为了使用方便，可将上式用齐次坐标与矩阵形式表示为：

$$\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}\frac{1}{dx}&0&u_0\\0&\frac{1}{dy}&v_0\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}$$

为了让你更直接的理解这一块内容，我们举个例子，由于被摄像机摄物体的图像经过镜头投影到CCD芯片上(像平面)：

我们设CCD的大小为$8×6mm$,而拍摄到的图像大小为$640×480$，则$dx=\frac{1}{80}mm$/像素，$dy=\frac{1}{80}mm$/像素,$u_0=320$,$v_0=240$。

上面的矩阵公式运用了齐次坐标，初学者可能会感到有些迷惑。大家会问：怎样将普通坐标转换为齐次坐标呢？齐次坐标能带来什么好处呢？

这里对齐次坐标做一个通俗的解释。此处只讲怎么将普通坐标改写为齐次坐标及为什么引入齐次坐标。这里只做一个通俗但不太严谨的表述。力求简单明了。针对齐次坐标的严谨的纯数学推导，可参见“周兴和版的《高等几何》---1.3拓广平面上的齐次坐标”。玉米曾详细读过《高等几何》这本书，但觉得离计算机视觉有点远，是讲纯数学的投影关系的，较为生涩难懂。

 齐次坐标可以理解为在原有坐标后面加一个“小尾巴”。将普通坐标转换为齐次坐标，通常就是在增加一个维度，这个维度上的数值为1。如图像坐标系$(u,v)$转换为$(u,v,1)$一样。对于无穷远点，小尾巴为0。注意，给零向量增加小尾巴，数学上无意义。

那么，为什么计算机视觉在坐标运算时要加上这个“小尾巴”呢？

如果用普通坐标来表达的话，会是下面的样子：

$$\begin{bmatrix}u\\v\end{bmatrix}=\begin{bmatrix}\frac{1}{dx}&0\\0&\frac{1}{dy}\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}+\begin{bmatrix}u_0\\v_0\end{bmatrix}$$

这样的运算形式会给后面的运算带来一定的麻烦，所以齐次坐标是一个更好的选择。

齐次坐标还有一个重要的性质，伸缩不变性。即：设齐次坐标$M$，则$αM=M$。

我们介绍过了像素坐标系之后，我们在此三大坐标系的问题上。我们想知道这三个坐标系有什么样的关系，我们先从下图说起：

图中显示，世界坐标系通过刚体变换到达摄像机坐标系，然后摄像机坐标系通过透视投影变换到达图像坐标系。可以看出，世界坐标与图像坐标的关系建立在刚体变换和透视投影变换的基础上。

首先，让我们来看一下刚体变换是如何将世界坐标系与图像坐标系联系起来的吧。这里，先对刚体变换做一个介绍：

刚体变换(regidbody motion)：三维空间中， 当物体不发生形变时，对一个几何物体作旋转， 平移的运动，称之为刚体变换。

因为世界坐标系和摄像机坐标都是右手坐标系，所以其不会发生形变。我们想把世界坐标系下的坐标转换到摄像机坐标下的坐标，如下图所示，可以通过刚体变换的方式。空间中一个坐标系，总可以通过刚体变换转换到另外一个个坐标系的。

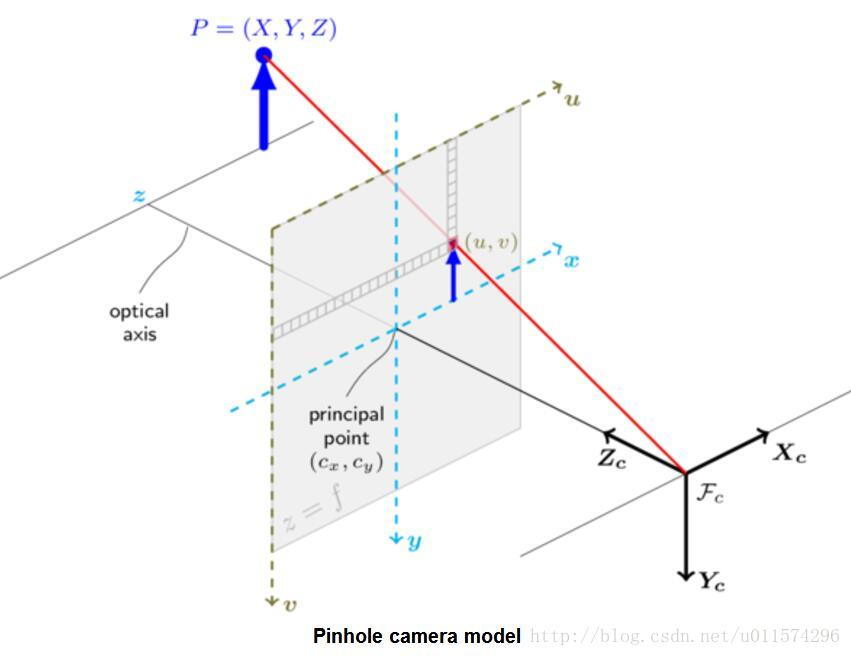
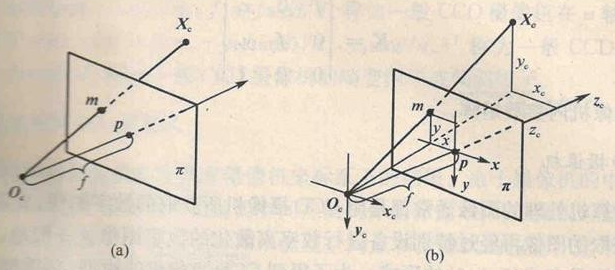
下面看一下，二者之间刚体变换的数学表达：

$$\begin{bmatrix}X_c\\Y_c\\Z_c\end{bmatrix}=\begin{bmatrix}r_{00}&r_{01}&r_{02}\\r_{10}&r_{11}&r_{12}\\r_{20}&r_{21}&r_{22}\end{bmatrix}\begin{bmatrix}X_w\\Y_w\\Z_w\end{bmatrix}+\begin{bmatrix}T_x\\T_y\\T_z\end{bmatrix}$$

对应的齐次表达式为：

$$\begin{bmatrix}X_c\\Y_c\\Z_c\\1\end{bmatrix}=\begin{bmatrix}R&t\\0_3^T&1\end{bmatrix}\begin{bmatrix}X_w\\Y_w\\Z_w\\1\end{bmatrix}=\begin{bmatrix}r_1&r_2&r_3&t\end{bmatrix}\begin{bmatrix}X_w\\Y_w\\0\\1\end{bmatrix}=\begin{bmatrix}r_1&r_2&t\end{bmatrix}\begin{bmatrix}X_w\\Y_w\\1\end{bmatrix}$$

其中，$R$是$3×3$的正交单位矩阵（即旋转矩阵），$t$为平移向量，$R$、$t$与摄像机无关，所以称这两个参数为摄像机的外参数(extrinsic parameter)，可以理解为两个坐标原点之间的距离，因其受$x$,$y$,$z$三个方向上的分量共同控制，所以其具有三个自由度。

我们假定在世界坐标系中物点所在平面过世界坐标系原点且与$Z_w$轴垂（也即棋盘平面与$X_w$-$Y_w$平面重合，目的在于方便后续计算），则$Z_w=0$。

首先，让我们来看一下透视投影是如何将摄像机坐标系与图像坐标系联系起来的吧。这里，先对透视投影做一个介绍：

透视投影(perspective projection)： 用中心投影法将形体投射到投影面上，从而获得的一种较为接近视觉效果的单面投影图。有一点像皮影戏。它符合人们心理习惯，即离视点近的物体大，离视点远的物体小，不平行于成像平面的平行线会相交于消隐点(vanish point)

这里我们还是拿针孔成像来说明（除了成像亮度低外，成像效果和透视投影是一样的，但是光路更简单）

下图是针kong-摄像机的基本模型。平面$π$称为摄像机的像平面，点$O_c$称为摄像机中心（或光心），$f$成为摄像机的焦距，$O_c$为端点且垂直于像平面的射线成为光轴或主轴，主轴与像平面的交点$p$是摄像机的主点。

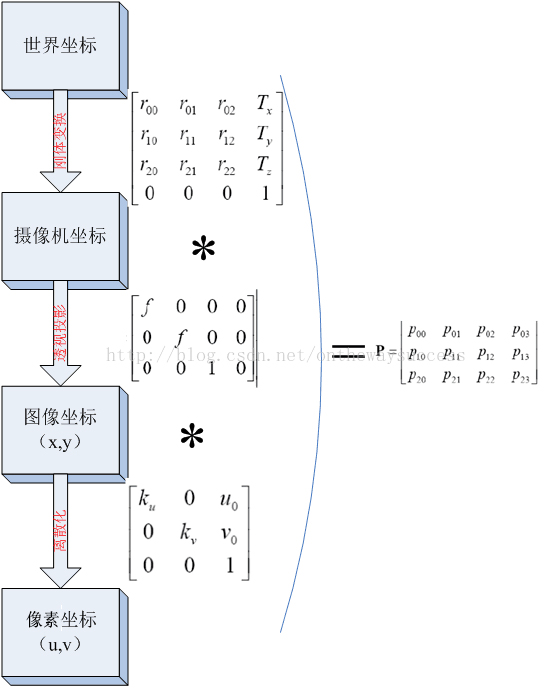
如图所示，图像坐标系为$o$-$xy$，摄像机坐标系为$O_c$-$x_cy_cz_c$。记空间点$X_c$摄像机坐标系中的齐次坐标为: $$X_c=\begin{bmatrix}x_c&y_c&z_c&1\end{bmatrix}^T$$

它的像点$m$在图像坐标系中的齐次坐标记为：

$$m=\begin{bmatrix}x&y&1\end{bmatrix}^T$$

根据三角形相似原理，可得：

$$x=\frac{fx_c}{z_c}$$

$$y=\frac{fy_c}{z_c}$$

我们使用矩阵表示为： $$z_c\begin{bmatrix}x\\y\\1\end{bmatrix}=\begin{bmatrix}f&0&0&0\\0&f&0&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}x_c\\y_c\\z_c\\1\end{bmatrix}=\begin{bmatrix}f&0&0\\0&f&0\\0&0&1\end{bmatrix}\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}x_c\\y_c\\z_c\\1\end{bmatrix}$$

注意由于齐次坐标的伸缩不变性，$z_c\begin{bmatrix}x&y&1\end{bmatrix}^T$和$\begin{bmatrix}x&y&1\end{bmatrix}^T$表示的是同一点。

我们已经介绍了各个坐标系之间的转换过程，但是我们想知道的是如何从世界坐标系转换到像素坐标系，因此我们需要把上面介绍到的联系起来：

将三者相乘，可以把这三个过程和在一起，写成一个矩阵：

$$z_c\begin{bmatrix}u\\v\\1\end{bmatrix}=z_c\begin{bmatrix}\frac{1}{d_x}&0& u_0\\0&\frac{1}{d_y}&v_0\\0&0&\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}=\begin{bmatrix}\frac{1}{d_x}&0&u_0\\0&\frac{1}{d_y}&v_0\\0&0&1\end{bmatrix}\begin{bmatrix}f&0&0&0\\0&f&0&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}x_c\\y_c\\z_c\\1\end{bmatrix}$$

$$=\begin{bmatrix}\frac{1}{d_x}&0& u_0\\0&\frac{1}{d_y}&v_0\\0&0&1\end{bmatrix}\begin{bmatrix}f&0&0&0\\0&f&0&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}r_{00}&r_{01}&r_{02}&T_x\\r_{10}&r_{11}&r_{12}&T_y\\r_{20}&r_{21}&r_{22}&T_z\\0&0&0&1\end{bmatrix}\begin{bmatrix}x_w\\y_w\\z_w\\1\end{bmatrix}$$

我们取世界坐标到图像坐标变换矩阵P如下：

$P=\begin{bmatrix}\frac{1}{d_x}&0& u_0\\0&\frac{1}{d_y}&v_0\\0&0&1\end{bmatrix}\begin{bmatrix}f&0&0&0\\0&f&0&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}r_{00}&r_{01}&r_{02}&T_x\\r_{10}&r_{11}&r_{12}&T_y\\r_{20}&r_{21}&r_{22}&T_z\\0&0&0&1\end{bmatrix}$

P就表示了一个投影相机，有下面公式：

其中：

$P=\begin{bmatrix}P_{00}&P_{01}&P_{02}&P_{03}\\P_{10}&P_{11}&P_{12}&P_{13}\\P_{20}&P_{21}&P_{22}&P_{23}\end{bmatrix}$

我们设：

$k_u=\frac{1}{d_x}$$k_v=\frac{1}{d_y}+v_0$

最后用一幅图来总结从世界坐标系到像素坐标系（不考虑畸变）的转换关系：

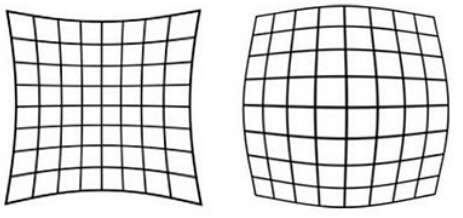
我们在摄像机坐标系到图像坐标系变换时谈到透视投影。摄像机拍照时通过透镜把实物投影到像平面上，但是透镜由于制造精度以及组装工艺的偏差会引入畸变，导致原始图像的失真。因此我们需要考虑成像畸变的问题。

透镜的畸变主要分为径向畸变和切向畸变，还有薄透镜畸变等等，但都没有径向和切向畸变影响显著，所以我们在这里只考虑径向和切向畸变。

顾名思义，径向畸变就是沿着透镜半径方向分布的畸变，产生原因是光线在原理透镜中心的地方比靠近中心的地方更加弯曲，这种畸变在普通廉价的镜头中表现更加明显，径向畸变主要包括桶形畸变和枕形畸变两种。以下分别是枕形和桶形畸变示意图：

它们在真实照片中是这样的：

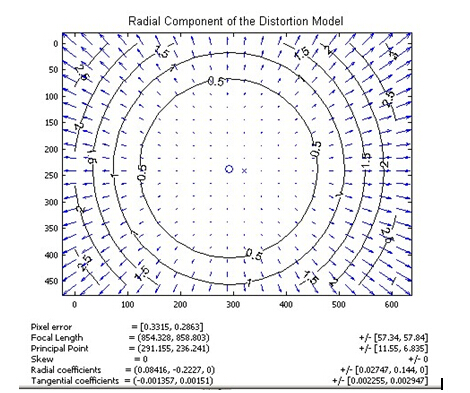
像平面中心的畸变为0，沿着镜头半径方向向边缘移动，畸变越来越严重。畸变的数学模型可以用主点（principle point）周围的泰勒级数展开式的前几项进行描述，通常使用前两项，即$k_1$和$k_2$，对于畸变很大的镜头，如鱼眼镜头，可以增加使用第三项$k_3$来进行描述，成像仪上某点根据其在径向方向上的分布位置，调节公式为：

$$x_0=x(1+k_1r^2+k_2r^4+k_3r^6)$$

$$y_0=y(1+k_1r^2+k_2r^4+k_3r^6)$$

式里$(x_0,y_0)$是畸变点在像平面的原始位置，$(x,y)$是畸变较正后新的位置，下图是距离光心不同距离上的点经过透镜径向畸变后点位的偏移示意图，可以看到，距离光心越远，径向位移越大，表示畸变也越大，在光心附近，几乎没有偏移。

切向畸变是由于透镜本身与相机传感器平面（像平面）或图像平面不平行而产生的，这种情况多是由于透镜被粘贴到镜头模组上的安装偏差导致。畸变模型可以用两个额外的参数$p_1$和$p_2$来描述：

$$x_0=2p_1xy+p_2(r^2+2x^2)+1$$

$$y_0=p_2(r^2+2y^2)+2p_2xy+1$$

下图显示某个透镜的切向畸变示意图，大体上畸变位移相对于左下——右上角的连线是对称的，说明该镜头在垂直于该方向上有一个旋转角度。

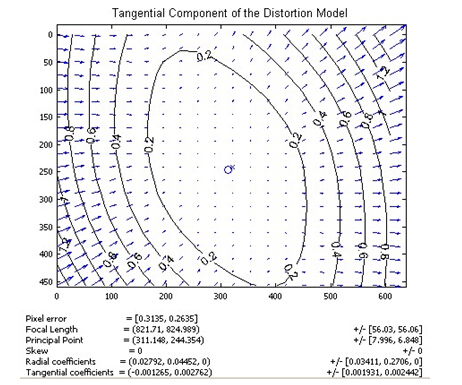
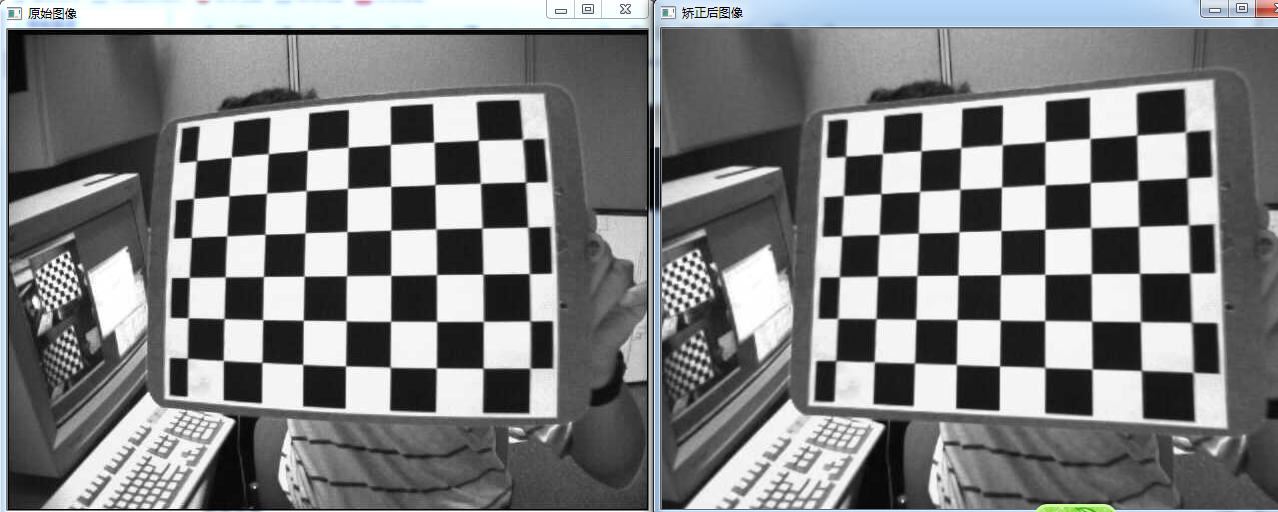
径向畸变和切向畸变模型中一共有5个畸变参数，在Opencv中他们被排列成一个$5×1$的矩阵，依次包含$k_1$、$k_2$、$p_1$、$p_2$、$k_3$，经常被定义为Mat矩阵的形式，如Mat distCoeffs=Mat（1,5，CV_32FC1，Scalar::all（0））；这5个参数就是相机标定中需要确定的相机的5个畸变系数。求得这5个参数后，就可以校正由于镜头畸变引起的图像的变形失真，下图显示根据镜头畸变系数校正后的效果：

相机标定的目的就是建立摄像机图像像素位置与物体空间位置之间的关系，即世界坐标系与图像坐标系之间的关系。方法就是根据摄像机模型，由已知特征点的坐标求解摄像机的模型参数，从而可以从图像出发恢复出空间点三维坐标，即三维重建。所以要求解的参数包括4个内参数和5个畸变参数，还有外部参数旋转矩阵和平移矩阵。

“张氏标定”是指张正友教授于1998年提出的单平面棋盘格的摄像机标定方法。张氏标定法已经作为工具箱或封装好的函数被广泛应用。张氏标定的原文为“A Flexible New Technique forCamera Calibration”。此文中所提到的方法，为相机标定提供了很大便利，并且具有很高的精度。从此标定可以不需要特殊的标定物，只需要一张打印出来的棋盘格。

上文中我们已经得到了像素坐标系和世界坐标系下的坐标映射关系，我们假设标定棋盘位于世界坐标中zw=0平面，则化简前文中的公式：

$$z_c\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}f_x&\gamma&u_0\\0&f_y&v_0\\0&0&1\end{bmatrix}\begin{bmatrix}r_{00}&r_{01}&r_{02}&T_x\\r_{10}&r_{11}&r_{12}&T_y\\r_{20}&r_{21}&r_{22}&T_z\\0&0&0&1\end{bmatrix} \begin{bmatrix}x_w\\y_w\\0\\1\end{bmatrix}=\begin{bmatrix}f_x&\gamma&u_0\\0&f_y&v_0\\0&0&1\end{bmatrix}\begin{bmatrix}r_{00}&r_{01}&T_x\\r_{10}&r_{11}&T_y\\r_{20}&r_{21}&T_z\end{bmatrix} \begin{bmatrix}x_w\\y_w\\1\end{bmatrix} $$

$$=\begin{bmatrix}f_x&\gamma&u_0\\0&f_y&v_0\\0&0&1\end{bmatrix} \begin{bmatrix}r_1&r_2&t\end{bmatrix} \begin{bmatrix}x_w\\y_w\\1\end{bmatrix}$$

其中，$u$,$v$表示像素坐标系中的坐标，$f_x=\frac{f}{dx}$,$f_y=\frac{f}{dy}$,$u_0$,$x_0$,γ(由于制造误差产生的两个坐标轴偏斜参数，通常很小，如果按上文中矩阵运算得到的值即为0）表示5个相机内参,$R$,$t$示相机外参,$x_w$,$y_w$,$z_w$ 表示世界坐标系中的坐标。

$f_x$,$f_y$和物理焦距f之间的关系为：$f_x=fs_x$和$f_y=fs_y$。其中$s_x=\frac{1}{dx}$表示$x$方向上的1毫米长度所代表像素值，即像素/单位毫米，$fx$,$fy$是在相机标定中整体计算的，而不是通过该公式计算的。

单应性(在计算机视觉中被定义为一个平面到另一个平面的投影映射)矩阵定义为：

$$H=\begin{bmatrix}f_x&\gamma&u_0\\0&f_y&v_0\\0&0&1\end{bmatrix} \begin{bmatrix}r_1&r_2&t\end{bmatrix}$$

那么现在就有：

$$z_c\begin{bmatrix}u\\v\\1\end{bmatrix}=H\begin{bmatrix}x_w\\y_w\\1\end{bmatrix}$$

我们如果求取H的值？

大家可以分析一下，H是一个三$3×3$的矩阵，并且有一个元素是作为齐次坐标。因此，H有8个未知量待解。

$(x_w,y_w)$作为标定物的空间坐标，可以由设计者人为控制，是已知量。$(u,v)$是像素坐标，我们可以直接通过摄像机获得。对于一组对应$(x_w,y_w)$-$(u,v)$我们可以获得两组方程。

 现在有8个未知量需要求解，所以我们至少需要八个方程。所以需要四个对应点。四点即可算出，图像平面到世界平面的单应性矩阵$H$。

这也是张氏标定采用四个角点的棋盘格作为标定物的一个原因。张氏标定就是利用一张打印的棋盘格，然后对每个角点进行标记其在像素坐标系的像素点坐标，以及在世界坐标系的坐标，张氏标定证明通过4组以上的点就可以求解出H矩阵的值，但是为了减少误差，具有更强的鲁棒性，我们一般会拍摄许多张照片，选取大量的角点进行标定。具体过程如下：

张正友教授从数学推导上证明了张氏标定算法的可行性。但在实际标定过程中，一般使用最大似然估计进行优化。假设我们拍摄了$n$张标定图片，每张图片里有$m$个棋盘格角点。三维空间点$X_j(x_w,y_w,z_w)$经过相机内参$M$，外参$R$，$t$变换后得到的二维像素为$x’(u,v)$，假设噪声是独立同分布的，我们通过最小化$x_{ij}$(实际值：棋盘格角点在像素坐标系下的实际值), $x’$(估计值)的位置来求解上述最大似然估计问题：

$$\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}||x_{ij}-x'(M,R_i,t_i,X_j)||^2$$

现在我们来考虑透镜畸变的影响，由于径向畸变的影响相对较明显，所以主要考虑径向畸变参数，根据经验，通常只考虑径向畸变的前两个参数$k_1$,$k_2$就可以（增加更多的参数会使得模型变的复杂且不稳定）。实际求解中，通常把$k_1$,$k_2$也作为参数加入上述函数一起进行优化，待优化函数如下所示：

$$\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}||x_{ij}-x'(M,k_1,k_2,R_i,t_i,X_j)||^2$$

极大似然估计是一种估计总体未知参数的方法。它主要用于点估计问题。所谓点估计是指用一个估计量的观测值来估计未知参数的真值。说穿了就一句话：就是在参数空间中选取使得样本取得观测值的概率最大的参数。

这里我没有过多的介绍张氏标定法的数学推导过程，感兴趣的童鞋可以看一下博客最后给出来的链接。

假设我们已经通过LM求得了相机的内参$M$和外参$R$,$t$。那如果获取到图像中二维坐标，如何获取到现实中三维坐标呢？当然单目摄像机无法获取三维坐标，但能反映一定关系。综上来讲，矩阵变换公式为：

根据坐标系之间转化和相机模型，研究了极几何及基本矩阵的知识，证明了基本矩阵是求得摄像机投影矩阵的关键，根据基础矩阵F和摄像机标定阶段获取的内参数矩阵$M$，计算得到本征矩阵$E$，通过对$E$进行奇异值分解求得外参数矩阵$R$，$t$，接着求出投影矩阵$P_1$和$P_2$、重投影矩阵$Q$。OpenCV提供了两个相关的函数stereoCalibrate()和stereoRectify()。

这三个基础的问题就决定了使用Opencv实现张正友法标定相机的标定流程、标定结果评价以及使用标定结果矫正原始图像的完整流程：

准备标定图片

标定图片需要使用标定板在不同位置、不同角度、不同姿态下拍摄，最少需要3张，以10~20张为宜。标定板需要是黑白相间的矩形构成的棋盘图，制作精度要求较高。

这里我们使用OpenCV提供的sample程序中的标定图片，图片位于opencv(C++版本)的安装路径：opencv\sources\samples\data下：

我们先创建一个C++控制台项目，并把标定图片按如下格式存放：

sample文件夹下有两个文件夹left和right，分别对应左摄像头和右摄像头拍摄到的标定板图片：

filename.txt存放标定图片的路径，内容如下：

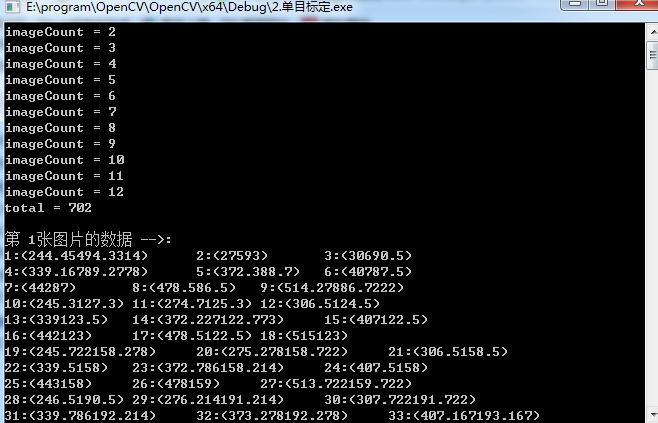
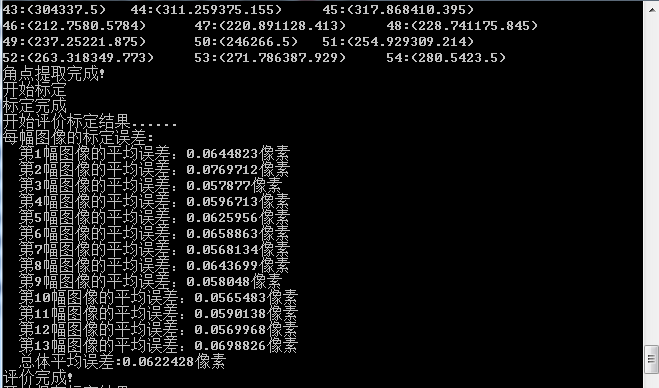
关于OpenCV提供的用于相机标定的API函数可以查看博客双目视觉标定程序讲解，单目标定的代码如下：

参数说明：

cameraMatrix：输入相机内参矩阵$$M=\begin{bmatrix}f_x&0&u_0\\0&f_y&v_0\\0&0&1\end{bmatrix}$$

distCoeffs：输入参数，相机的畸变系数$$(k_1,k_2,p_1,p_2[,k_3[,k_4,k_5,k_6[,s_1,s_2,s_3,s_4[,τ_x,τ_y]]]])$$

有4，5,8,12或14个元素。如果这个向量是空的，就认为是零畸变系数。

$R$：可选的立体修正变换矩阵，是个$3×3$的矩阵。

在单目相机例子中，$R$就设置为单位矩阵cv::Mat R = cv::Mat::eye(3, 3, CV_32F)，表示不进行立体校正。

在双目相机例子中，newCameraMatrix一般是用cv::stereoRectify()计算而来的，设置为$R_1$或$R_2$(左右相机平面行对准的校正旋转矩阵)。此外，根据$R$，新的相机在坐标空间中的取向是不同的。例如，它帮助配准双目相机的两个相机方向，从而使得两个图像的极线是水平的，且$y$坐标相同（在双目相机的两个相机谁水平放置的情况下）。

newCameraMatrix：新的相机内参矩阵

$$M=\begin{bmatrix}f_x'&0&u_0'\\0&f_y'&v_0'\\0&0&1\end{bmatrix}$$

在单目相机例子中，newCameraMatrix一般和cameraMatrix相等，或者可以用cv::getOptimalNewCameraMatrix()来计算，获得一个更好的有尺度的控制结果。

在双目相机例子中，newCameraMatrix一般是用cv::stereoRectify()计算而来的，设置为$P_1$或$P_2$(左右相机把空间3D点的坐标转换到图像的2D点的坐标的投影矩阵)。

函数功能：重映射：就是把一幅图像中某位置的像素放置到另一个图片指定位置的过程。

参数说明：

（1）INTER_NEAREST——最近邻插值

（2）INTER_LINEAR——双线性插值（默认）

（3）INTER_CUBIC——双三样条插值（默认）

（4）INTER_LANCZOS4——lanczos插值（默认）

程序运行后，把相机内部参数和外部参数保存在caliberation_result.txt文件中，内容如下：

下面在附上一份来自于其他博客的源码：