机器学习入门：L1范数最小正则化通俗易懂的理解

对于L1范数最小正则化，我们先拆分开来解释。 L1范数：向量中各元素绝对值之和。如[1,-1,3]的L1范数为1+1+3=5。 正则化：对模型提高泛化能力的一种方案。对于训练得到的模型，可能会出现模型复杂的情况，正则化可以看作对模型的简化，以提高模型适应能力。 最小：指最小化损失函数。在我们训练模型时，通过最小化损失函数可以使模型对于训练集更为拟合。

那么对于L1范数最小正则化的理解可以是这样的：向损失函数J中添加一个L1范数，使 J1=J+L1_norm， 将新的损失函数J1作为新的优化目标，J1最小时，能够得到具有泛化能力的模型（正则化）。

实际上，L1范数最小正则化是一个能使训练的模型具有泛化能力，且能获得稀疏解的一种方案。

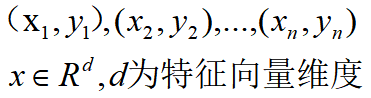首先我们假设有一组训练集: 对于这一组训练集，我们希望得到一个权重向量w，使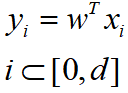： 在谈到拟合问题时，我们希望（yi - wTxi）尽量小，基于最小二乘法，可以构建以下方程： 对于上述方程，Jemp可以作为损失函数，在我们把Jemp作为优化目标时，优化结果为：所有训练集都能很好地拟合得到结果，但不具备泛化能力。得到的权重向量 w 并不唯一，更可能会出现 w 向量内单个维度绝对值特别大的情况，这种情况下，某个维度特征的微弱变化会引起结果病态的变化。显然，得到的结果是不具备实际意义的。

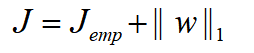此时，我们引入L1范数会得到什么样的改观呢？ 在Jemp的基础上加上 w 的L1范数。将 J 作为优化目标，对 w 单个维度绝对值过大加入了一个“惩罚”，可以有效防止这种情况。 另一方面，L1范数最小正则化可以获得稀疏解。即 w 的解中，很多维度的数值为0。稀疏解的存在舍弃了样本中不影响结果或者影响微弱的特征，能够有效地简化模型。（为什么能获得稀疏解在下一节介绍）

那么，通过引入L1范数，最终得到的模型不仅能够迎合训练集，而且足够简单有效，这也就是说为什么L1范数最小正则化能够泛化模型。

或许用一个简单的例子就能帮助我们理解了。 假设在一个二维空间，我们有样本点 (2,2)。已知模型是线性模型。 即：y = ax+b 代入样本点：2 = 2a+b 那么 a , b 作为这个模型的解，解空间为： b = 2 - 2 a ，解空间如图所示。b 为 y 轴。 对于这个解空间来说，可以知道，a ，b的解是不固定的。甚至 a , b的绝对值也特别大。 而当我们引入L1范数，[a , b]视为解向量 w 。||w||1 = |a|+|b|。对于L1范数在坐标系中的表示即为如图所示的一个菱形（每个角均为90°）。 而当这个菱形与a,b的解空间有交点时，意味着引入L1范数的损失函数有解。此时，我们需要损失函数最小化，这是一个凸优化问题，在极值处可以求得解。即当菱形与蓝色直线只有一个交点时，可以得到我们的基于L1范数最小正则化的解。 那么最终我们得到的解为 a=1,b=0，最终得到的拟合模型为 y = x。其中b为0恰好某种意义满足了稀疏解的性质，这是由于L1范数本身性质，以至于当存在最优解时，这个解往往是“顶点”，而这个“顶点”，恰好满足解向量多个维度值为0的情况。（放大到多维空间也是同样的）

那么，重申结论：L1范数最小正则化在一般情况下是能够得到稀疏解的。

实际上，如果使用其他的范数作为辅助优化项呢？ 从上图可以看出，当使用其他的Lp范数时，p值越小，顶点越尖锐。那么此时能够得到稀疏解的可能性越大。而我们为什么要使用L1范数呢，这是由于它方便计算这个性质决定的。