| float浮点数精度丢失问题分析 | 您所在的位置:网站首页 › float不精确 › float浮点数精度丢失问题分析 |
float浮点数精度丢失问题分析
|
前言 最近在研究如何在UE4的游戏引擎中搭建出地球,从而承载地图可视化的内容。粗略来讲,地球可以被视为一个半径6371km的球体,而UE4中一个单位代表真实世界的1cm,因此如果要制作一个1:1还原世界的地球,映射到UE4世界中地球半径为637100000个单位,使用三维直角坐标系表示球面上的点,每个分量也需要千万、亿级别的表达。 依照这种逻辑制作出的地球,当摄像机在地面上空漫游运动时,会发现摄像机出现了无法控制的抖动,究其原因,UE4中表示位置使用的都是float类型的FVector,过大的数量级导致了精度丢失。为了解决这个问题,需要从原理上理解float,才能分析问题产生的根本原因。 思考int,float,double这些类型编码时频繁使用,但具体的存储方式却关注的很少。我们知道int和float类型都使用4字节32位二进制进行存储,因此可以先做一个横向对比: int是有符号整型,先不考虑符号位以及补码表示等概念,每一位2进制只有0和1两种选择,因此int型最多能表达 2^{32} 个整数,这与int能够表达[-2^{31},2^{31} - 1]范围内共2^{32}个整数吻合。 float同样也使用4字节存储,但除了整数外还能够存储小数位,并且表示的范围比int还要更大。这就带来了一些思考:float一定是使用了与int不同的存储方式,才能存储更多的数据,这种方式优点十分明显,但是否也有其局限性和缺点。 float存储方式与int的存储方式不同,float为了支持小数,因此采用科学记数法进行数据的表示。在十进制中,一个科学计数法的数字可以被写为 \pm a.b \times10^{c} 的形式, a 是1-9中的一个整数。 推演到二进制中,一个科学计数法的数字可以被写为 \pm a.b \times2^{c} 的形式,因为a 只能取1,所以可以节省一位,表达为\pm 1.b \times2^{c},因此float需要存储的内容有以下三部分: \pm :符号位(sign),占1位,表示浮点数的正负,定义0为正,1为负。c :指数位(exponent),占8位,采用无符号整数表示 0~255共256个数字。为了表示无符号整数,实际是对数字做了偏移+127处理,因此127表示的是0。除了预留全0和全1两个数字外(即0和255,预留用作特殊表示,会在下面的小节进行叙述),指数范围取值在-126 ~ +127这一区间,偏移完即1~254。b :尾数位(significand),占23位,加上显式的整数位,一共有24位的精度。以小数0.15625为例,可以按照这个规则,推导一下float的存储方式: 这里需要复习一下十进制小数写成二进制的规则,即”乘2取整,顺序排列“,通过不断的左移反推每一位小数。计算过程见下表: 剩余小数乘2取整数位0.156250.312500.31250.62500.6251.2510.250.500.511可见最后二进制小数结果为0.00101,为了调整成整数位为1的形式,需要左移3位,因此结果可以表示成 +1.01\times2^{-3} ,指数位做+127偏移得到结果124,即0111,1100,因此最后的32位结果如下图所示:  了解了存储方式后,就能够推导出float能够表达的数字范围了。指数偏移后最大为254,所以偏移前为127,尾数为全为1,因此最大和最小数字为 \pm1.11111111111111111111111\times2^{127},逼近 \pm2^{128} 2^{128} 转换为十进制为 3.4028236692093846346337460743177\times10^{38}。 因此通常说float表示的数字范围为 [-3.4\times10^{38}, 3.4\times10^{38}] 。 float表示一个整数的局限性根据上述讨论的记数方法,一个float数,由符号位决定正负,由尾数位决定数字构成,由指数位决定小数点在尾数上的左右移动。 尾数的23位加上显式为1的整数位共24位,而对于一个24位的二进制数,能够表示的最大数字为 2^{24}-1 ,转换为十进制为16777215,使用二进制科学计数法表示为 +1.11111111111111111111111\times2^{23} 。 从这里可以看到,小于16777215的整数,都能够靠尾数确定数字构成,指数控制小数点移动这种方式表示出来。 那大于16777215的整数呢? 16777216比较特殊,是 2^{24} ,因此可以表示为 +1.0\times2^{24} ,只靠控制指数位就表示了出来。 接下来看16777217,即 2^{24}+1 ,按照二进制规则可以写成1(23个0)1,共25位,转换为科学计数法时可以看到,最后的一个1在第25位,会被尾数位丢失掉,导致记录的数字还是16777216,造成了精度的丢失。在UE4中也可以进行验证,当将Camera的某一分量设置为16777217时,会被自动显示为16777216。 接下来看16777218,即 2^{24}+2 ,按照二进制规则可以写成1(22个0)10,共25位,转换为科学计数法时可以看到,因为1在第24位,因此没有被丢失造成精度丢失。 由此可知,并不是所有超过16777216的整数都会遇到精度丢失的问题。 实际上,16777218 / 2 = 8388609 = 8388608 + 1 = 2^{23}+1 ,二进制可以写成1(22个0)1,16777218尾数与其完全一致,只是通过指数位多移动了一位。所以,所有大于16777216的整数,只要能够表示为0~16777215之间一个数字进行移位( \times2^{n} )操作,就能够保证不丢失精度。 小于等于16777216的所有整数可以被精确表示,这就是float保证7位有效数字的原因。 float表示小数根据小数位的二进制表示方式我们可以知道,一个小数需要拆分为多个小数的加和形式。 以0.75为例,可以分解为0.5+0.25,转换为二进制即为0.11,但更多的小数会使得二进制表示无限循环,因为存储位数有限,从而只能逼近小数,造成精度误差。 以0.7为例,直接使用”乘2取整,顺序排列“后可以看到,结果为0.10接上1100的无限循环。 剩余小数乘2取整数位0.71.410.40.800.81.610.61.210.20.400.40.800.81.610.61.210.20.400.40.80下图是IEEE754给出的float和double精度范围 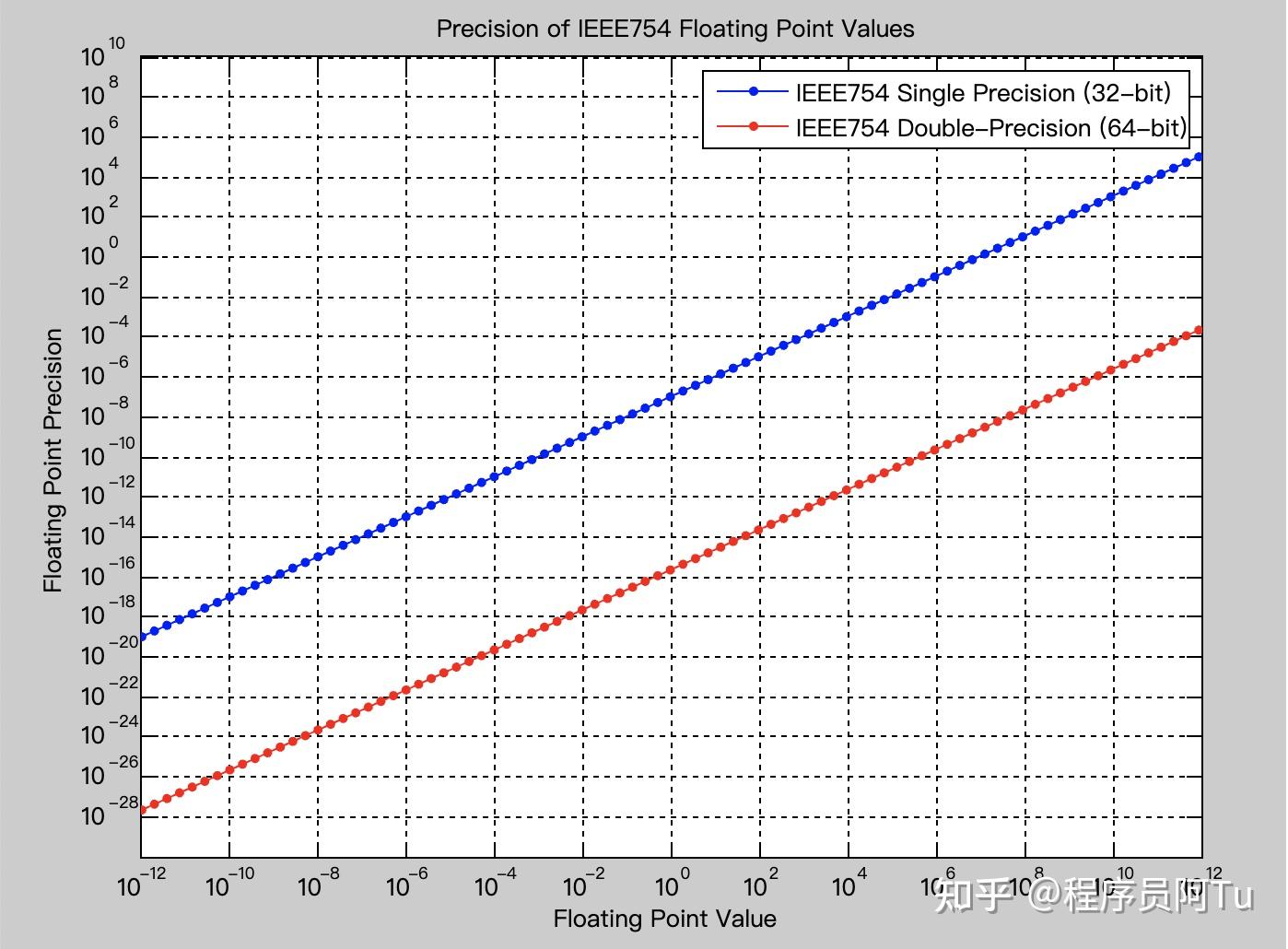 可以看到,当float数字在千万级别时,精度是1,即已经无法感知到小数位的变化。 为了达到小数点后一位的精度,至少要保证float数字在百万以内,如果需要更高精度,就要根据图表控制float数字的数量级。 这是在不使用double的情况下唯一可以解决精度丢失问题的方法。 附:float指数位预留值前面说到指数位预留了全0和全1,实际上是用来表示float的0、无穷以及NaN(Not a Number)等情况,用于覆盖无法直接用科学记数法表示的情况,具体的所有情况可以看下面的表格。 指数位尾数位为0尾数位不为0全00非标准值其他标准值标准值全1±∞NaN其中非标准值用于扩充 2^{-126} 情况下整数位为0的情况,当尾数位是 b 时,表示的非标准值为 \pm0.b\times2^{-126} ,使得最趋近于0的值为 2^{-149}\approx1.4\times10^{-45} 。 . |
【本文地址】
| 今日新闻 |
| 推荐新闻 |
| 专题文章 |