5.4 三角函数的图像与性质

\({\color{Red}{欢迎到学科网下载资料学习 }}\) [ 【高分突破系列】高一数学上学期同步知识点剖析精品讲义与分层练习] (https://www.zxxk.com/docpack/2783085.html) \({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)

必修第一册同步拔高练习，难度3颗星！

一般地，对于函数\(f(x)\)，如果存在一个非零常数\(T\)，使得定义域内的每一个\(x\)值，都满足\(f(x+T)=f(x)\)，那么函数\(f(x)\)就叫做周期函数，\(T\)叫做该函数的周期. \({\color{Red} {PS }}\) ①从解析式\(f(x+T)=f(x)\)来看：任一自变量\(x\)对应函数值\(y\)与\(x\)增加\(T\)后对应函数值相等； ②从图象看：整体函数图象是由一部分图象像“分身术”一样向两边延申，而那一部分图象的水平长度就是其正周期！

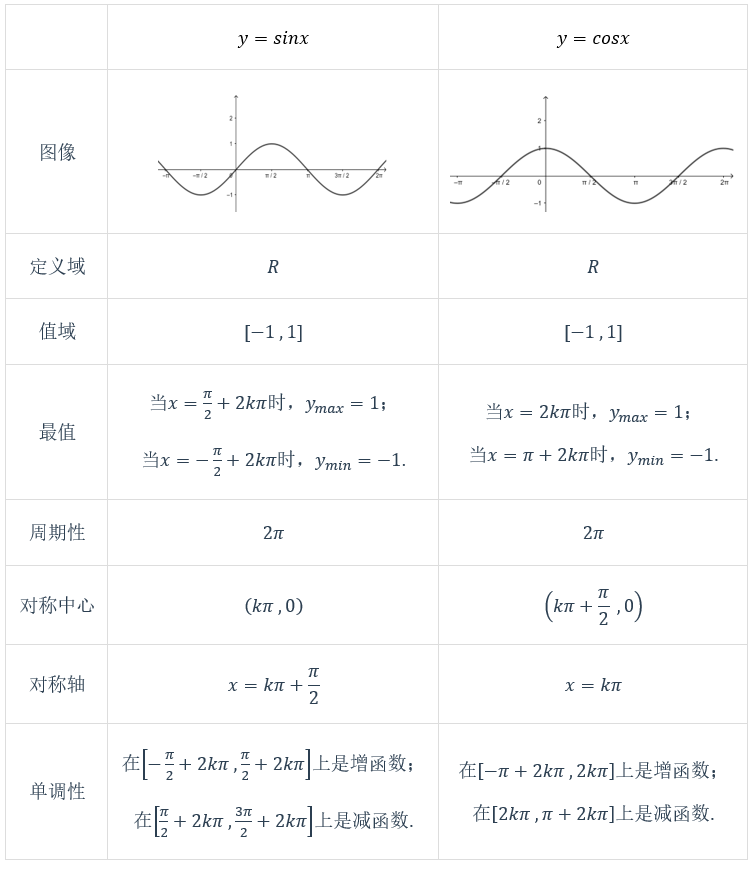
③ 三角函数就是典型的周期函数.  

\({\color{Red} { 注}}\) 表中的\(k∈Z\)

\({\color{Red} {注}}\) 表中的\(k∈Z\)  

【典题1】 \(f(x)=|\sin x|+|\cos x|\)的最小正周期是(　　) A.\(\dfrac{\pi}{2}\) \(\qquad \qquad \qquad \qquad\) B.\(π\) \(\qquad \qquad \qquad \qquad\) C.\(2π\) \(\qquad \qquad \qquad \qquad\)D.\(3π\) 【解析】\(f\left(x+ \dfrac{\pi}{2}\right)=\left|\sin \left(x+\dfrac{\pi}{2}\right)\right|+\left|\cos \left(x+\dfrac{\pi}{2}\right)\right|\)\(=|\cos x|+|\sin x|=f(x)\), 故\(\dfrac{\pi}{2}\)是\(y=f(x)\)的周期，由选项可知选\(A\). 【点拨】从定义出发：存在一个非零常数\(T\)，使得定义域内的每一个\(x\)值，都满足\(f(x+T)=f(x)\)，则\(T\)叫做该函数的周期.  

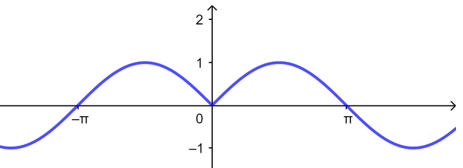
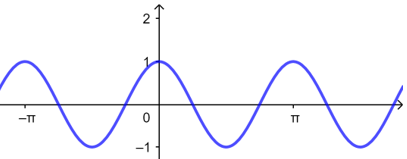
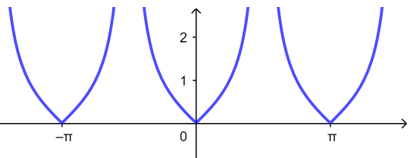
【典题2】下列函数中，最小正周期为\(\dfrac{\pi}{2}\)的是(　　) A．\(y=\sin|x|\) \(\qquad \qquad\)B．\(y=\cos|2x|\)\(\qquad \qquad\) C．\(y=|\tan x|\) \(\qquad \qquad\)D．\(y=|\sin2x|\) 【解析】由图可知函数\(y=\sin|x|\)不是周期函数，故\(A\)不正确；

由于函数\(y=\cos|2x|=\cos2x\)的周期为\(\dfrac{2 \pi}{2}=\pi\)，故\(B\)不正确；

由图可知函数\(y=|\tan x|\)的周期\(T=π\)，故\(C\)不正确；

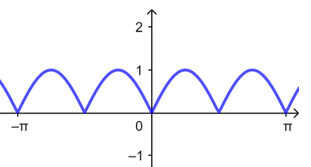
由图可知函数\(y=|\sin2x|\)的周期为\(T=\dfrac{\pi}{2}\)，故\(D\)正确，

故选：\(D\)． 【点拨】 ① 函数\(f(x)=A\sin(ωx+φ)\), \(f(x)=A\cos(ωx+φ)\)的最小正周期\(T=\dfrac{2 \pi}{\omega}\)，函数\(f(x)=A\tan(ωx+φ)\)的最小正周期\(T=\frac{\pi}{\omega}\)； ② 利用函数的对称变换与翻转变换，利用图象判断函数周期更容易些.  

【典题1】 函数\(y=\sin \left(2 x+\dfrac{\pi}{3}\right)\)的图象(　　) A．关于点\(\left(\dfrac{\pi}{6}, 0\right)\)对称 \(\qquad \qquad \qquad \qquad\) B．关于点\(\left(\dfrac{\pi}{3}, 0\right)\)对称 C．关于直线\(x=\dfrac{\pi}{6}\)对称 \(\qquad \qquad \qquad \qquad\)D．关于直线\(x=\dfrac{\pi}{3}\)对称 【解析】 \({\color{Red} {方法1 }}\)对于函数\(y=\sin \left(2 x+\dfrac{\pi}{3}\right)\)， \({\color{Red} { (求出函数的所有对称轴和对称中心再判断)}}\) 令\(2 x+\dfrac{\pi}{3}=\dfrac{\pi}{2}+k \pi\)，则\(x=\dfrac{\pi}{12}+\dfrac{k \pi}{2}\) , 则函数的对称轴是\(x=\dfrac{\pi}{12}+\dfrac{k \pi}{2}\left(k \in Z \right)\)， 若\(\dfrac{\pi}{12}+\dfrac{k \pi}{2}=\dfrac{\pi}{6}\)，解得\(k=\dfrac{1}{6} \notin Z\)，\(\dfrac{\pi}{12}+\dfrac{k \pi}{2}=\dfrac{\pi}{3}\)，\(k=\dfrac{1}{2} \notin Z\)，故排除\(C ,D\)； 令\(2 x+\dfrac{\pi}{3}=k \pi\)，则\(x=-\dfrac{\pi}{6}+\dfrac{k \pi}{2}\) , 则函数的对称中心是\(\left(-\dfrac{\pi}{6}+\dfrac{k \pi}{2}, 0\right) \left(k \in Z \right)\)， 若\(-\dfrac{\pi}{6}+\dfrac{k\pi}{2}=\dfrac{\pi}{6}\)，解得\(k=\dfrac{2}{3}\notin Z\),可排除\(A\); 若\(-\dfrac{\pi}{6}+\dfrac{k\pi}{2}=\dfrac{\pi}{3}\)，解得\(k=1\in Z\),故关于\((\dfrac{\pi}{3},0)\)对称. \({\color{Red} { 方法2}}\) 对于函数\(y=\sin \left(2 x+\dfrac{\pi}{3}\right)\)， 当\(x=\dfrac{\pi}{6}\)时，\(2 x+\dfrac{\pi}{3}=\dfrac{2 \pi}{3}\)，而\(\left(\dfrac{2 \pi}{3}, 0\right)\)不是正弦函数\(y=\sin x\)的对称中心，故\(A\)错误； 当\(x=\dfrac{\pi}{3}\)时，\(2 x+\dfrac{\pi}{3}=\pi\)，而是正弦函数\(y=\sin x\)的对称中心，故\(B\)正确； 当\(x=\dfrac{\pi}{6}\)时，\(2 x+\dfrac{\pi}{3}=\dfrac{2 \pi}{3}\)，而\(x=\dfrac{2π}{3}\)不是正弦函数\(y=\sin x\)的对称轴，故\(C\)错误； 当\(x=\dfrac{\pi}{3}\)时，\(2 x+\dfrac{\pi}{3}=\pi\)，而\(x=π\)不是正弦函数\(y=\sin x\)的对称轴，故\(D\)错误； 故选：\(B\)． 【点拨】本题两种方法， 方法1是求出三角函数的全部对称轴或对称中心(此时把\(ωx+φ\)看成整体)，再判断； 方法2是把问题转化正弦函数\(y=\sin x\)的性质判断； 对于三角函数\(f(x)=A \sin (\omega x+\varphi)+B\) ① 若\(x=x_0\)是其对称轴，则\(ωx_0+φ\)是正弦函数\(y=\sin x\)的对称轴； ② 若\((x_0,B)\)是其对称中心，则\((ωx_0+φ ,B)\)满足函数\(y=Asinx+B\)的对称中心. 对于三角函数\(f(x)=A\cos(ωx+φ)+B\)类似.  

【典题2】 已知函数\(f(x)=\cos (3 x+\varphi)\left(-\frac{\pi}{2}f(2)\) 【解析】\({\color{Red} { (显然选项是由函数单调性作出判断)}}\) 令\(-\dfrac{\pi}{2}+2 k \pi