| 三维特征描述子：PFH、FPFH、VFH、PPF | 您所在的位置：网站首页 › 3d形状有哪些的英文 › 三维特征描述子：PFH、FPFH、VFH、PPF |
三维特征描述子：PFH、FPFH、VFH、PPF
|
参考： https://segmentfault.com/a/1190000021430941http://www.pclcn.org/study/shownews.php?id=101https://blog.csdn.net/xinxiangwangzhi_/article/details/90023207https://blog.csdn.net/u011736771/article/details/85103293http://www.pclcn.org/study/shownews.php?id=95 引言 一堆离散的样点，只包含相对于某个坐标系下的位置参数，虽然能在空间中比较好的显示出物体的样子来，但对于视觉来说，这是远远不够的。之所以在文章的题目中提到特征，就是希望能用特征的方法，达到视觉识别的功能。离散点云，除了坐标信息外，最为直观的特征就是点、法向、曲率，这是最简单的特征，也是最忠实于原始点云的，这些特征包含了点云的最为详细的数据，虽然很少直接的使用，但在这个特征的基础上，可以实现更高层次的识别。计算简单，速度快是这些基础特征的特点之一，但是在进行物体识别的时候，在大场景中，拥有相似法向或曲率的区域太多了，这就从一定程度上削弱了它的作用。下面将会逐步介绍下PFH、 FPHF、VFH等特征的原理与PCL的实现方式。 1. PFH 1.1 PFH原理正如点特征表示法所示，表面法线和曲率估计是某个点周围的几何特征基本表示法。虽然计算非常快速容易，但是无法获得太多信息，因为它们只使用很少的几个参数值来近似表示一个点的k邻域的几何特征。然而大部分场景中包含许多特征点，这些特征点有相同的或者非常相近的特征值，因此采用点特征表示法，其直接结果就减少了全局的特征信息。本小节介绍三维特征描述子中的一位成员：点特征直方图(Point Feature Histograms)，我们简称为PFH，本小节将介绍它的理论优势，从PCL实现的角度讨论其实施细节。PFH特征不仅与坐标轴三维数据有关，同时还与表面法线有关。 PFH计算方式通过参数化查询点与邻域点之间的空间差异，并形成一个多维直方图对点的k邻域几何属性进行描述。直方图所在的高维超空间为特征表示提供了一个可度量的信息空间，对点云对应曲面的6维姿态来说它具有不变性，并且在不同的采样密度或邻域的噪音等级下具有鲁棒性。点特征直方图（PFH）表示法是基于点与其k邻域之间的关系以及它们的估计法线，简言之，它考虑估计法线方向之间所有的相互作用，试图捕获最好的样本表面变化情况，以描述样本的几何特征。因此，合成特征超空间取决于每个点的表面法线估计的质量。如图1所示，表示的是一个查询点(Pq) 的PFH计算的影响区域，Pq 用红色标注并放在圆球的中间位置，半径为r， (Pq)的所有k邻元素（即与点Pq的距离小于半径r的所有点）全部互相连接在一个网络中。最终的PFH描述子通过计算邻域内所有两点之间关系而得到的直方图，因此存在一个O(k) 的计算复杂性。 为了计算两点Pi和Pj及与它们对应的法线Ni和Nj之间的相对偏差，在其中的一个点上定义一个固定的局部坐标系，如图2所示。
有关其他详细信息，请见API文件。为查询点创建最终的PFH表示，所有的四元组将会以某种统计的方式放进直方图中，这个过程首先把每个特征值范围划分为b个子区间，并统计落在每个子区间的点数目，因为四分之三的特征在上述中为法线之间的角度计量，在三角化圆上可以将它们的参数值非常容易地归一到相同的区间内。一个统计的例子是：把每个特征区间划分成等分的相同数目，为此在一个完全关联的空间内创建有b个区间的直方图。在这个空间中，一个直方图中某一区间统计个数的增一对应一个点的四个特征值。如图3所示，就是点云中不同点的点特征直方图表示法的一个例子，在某些情况下，第四个特征量d在通常由机器人捕获的2.5维数据集中并不重要，因为临近点间的距离从视点开始是递增的，而并非不变的，在扫描局部点密度影响特征时，实践证明省略d是有益的。 点特征直方图（PFH）在PCL中的实现是pcl_features模块的一部分。默认PFH的实现使用5个区间分类（例如：四个特征值中的每个都使用5个区间来统计），其中不包括距离（在上文中已经解释过了——但是如果有需要的话，也可以通过用户调用computePairFeatures方法来获得距离值），这样就组成了一个125浮点数元素的特征向量（3^5），其保存在一个pcl::PFHSignature125的点类型中。以下代码段将对输入数据集中的所有点估计其对应的PFH特征。 #include //点类型头文件 #include //pfh特征估计类头文件 ...//其他相关操作 pcl::PointCloud::Ptrcloud(new pcl::PointCloud); pcl::PointCloud::Ptrnormals(new pcl::PointCloud()); ...//打开点云文件估计法线等 //创建PFH估计对象pfh，并将输入点云数据集cloud和法线normals传递给它 pcl::PFHEstimation pfh; pfh.setInputCloud(cloud); pfh.setInputNormals(normals); //如果点云是类型为PointNormal,则执行pfh.setInputNormals (cloud); //创建一个空的kd树表示法，并把它传递给PFH估计对象。 //基于已给的输入数据集，建立kdtree pcl::KdTreeFLANN::Ptrtree(new pcl::KdTreeFLANN()); pfh.setSearchMethod(tree); //输出数据集 pcl::PointCloud::Ptrpfhs(new pcl::PointCloud()); //使用半径在5厘米范围内的所有邻元素。 //注意：此处使用的半径必须要大于估计表面法线时使用的半径!!! pfh.setRadiusSearch(0.05); //计算pfh特征值 pfh.compute(*pfhs); // pfhs->points.size ()应该与input cloud->points.size ()有相同的大小，即每个点都有一个pfh特征向量PFHEstimation类的实际计算程序内部只执行以下： 对点云P中的每个点p： 得到p点的最近邻元素对于邻域内的每对点，计算其三个角度特征参数值将所有结果统计到一个输出直方图中使用下列代码，从一个k-邻域计算单一的PFH描述子： computePointPFHSignature (const pcl::PointCloud &cloud, const pcl::PointCloud &normals, const std::vector &indices, int nr_split, Eigen::VectorXf &pfh_histogram);此处，cloud变量是包含点的输入点云，normals变量是包含对应cloud的法线的输入点云，indices代表输入点云（点与法线对应）中查询点的k-近邻元素集，nr_split是所分区间的数目，用于每个特征区间的统计过程，pfh_histogram是浮点数向量来存储输出的合成直方图。 1.3 PFH的总结点特征的描述子一般是基于点坐标、法向量、曲率来描述某个点周围的几何特征。用点特征描述子不能提供特征之间的关系，减少了全局特征信息。因此诞生了一直基于直方图的特征描述子：PFH–point feature histogram（点特征直方图）。 PFH通过参数化查询点和紧邻点之间的空间差异，形成了一个多维直方图对点的近邻进行几何描述，直方图提供的信息对于点云具有平移旋转不变性，对采样密度和噪声点具有稳健性。PFH是基于点与其邻近之间的关系以及它们的估计法线，也即是它考虑估计法线之间的相互关系，来描述几何特征。 PFH的缺点： 计算复杂度高。已知点云P中有n个点，假设点云均匀密度，每点在邻域半径r内平均可以选到k个近邻，该算法对每个点来说计算PFH的时间复杂度为O(k^2)，那么它的点特征直方图（PFH）的理论计算复杂度就是 O(nk²)。对于实时应用或接近实时应用中，密集点云的点特征直方图（PFH）的计算，O(nk²)的计算复杂度实在不敢恭维，是一个主要的性能瓶颈。存在大量的重复计算。在PFH的三个特征元素的计算过程中，邻域内任意两点都需要计算一次三个特征元素值。这对于相邻的点来说，尽管他们的邻域不一定完全相同，但有很大的概率会同时包含某些近邻点（邻域半径的值越大，重复的近邻就越多）。这些被同时包含的近邻点之间的会被重复地配对在一起并计算特征元素值。虽然论文及PCL了中都引入了高速缓存机制，把重复的计算的花销改成查找的花销，但其效率依然没有太大的改观。 2. FPFH 2.1 FPFH原理快速点特征直方图(Fast Point Feature Histograms, FPFH)是PFH计算方式的简化形式。它的思想在于分别计算查询点的k邻域中每一个点的简化点特征直方图(Simplified Point Feature Histogram,SPFH)，再通过一个公式将所有的SPFH加权成最后的快速点特征直方图。FPFH把算法的计算复杂度降低到了O(nk) ，但是任然保留了PFH大部分的识别特性。 FPFH计算过程： 只计算每个查询点Pq和它邻域点之间的三个特征元素（参考PFH），在这里不同于PFH：PFH是计算邻域点所有组合的特征元素，而这一步只计算查询点和近邻点之间的特征元素。如下图，第一个图是PFH计算特征过程，即邻域点所有组合的特征值（图中所有连线，包括但不限于Pq和Pk之间的连线），第二个图是FPFH的计算内容，只需要计算Pq（查询点）和紧邻点（图2中红线部分）之间的特征元素。可以看出降低了复杂度我们称之为SPFH（simple point feature histograms）。  重新确定k近邻域，为了确定查询点Pq的近邻点Pk的SPFH值、查询点Pq和近邻的距离以及k的数值（一般使用半径kdtree搜索，只能确定某半径范围内的近邻点，不能确定具体的查询点与近邻的距离、k数值----PS：应该是这样，不过重新确定k近邻主要还是计算查询点Pq的近邻点Pk的SPFH值），则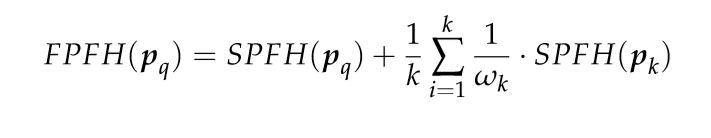：  其中Wk为权重，一般为距离，表示查询点p与给定度量空间中的近邻点pk之间的距离。
2.2 FPFH与PFH的主要区别
FPFH没有对全互连点的所有邻近点的计算参数进行统计，因此可能漏掉了一些重要的点对，而这些漏掉的对点可能对捕获查询点周围的几何特征有贡献。PFH特征模型是对查询点周围的一个精确的邻域半径内，而FPFH还包括半径r范围以外的额外点对（但不超过2r的范围）；因为采用权重计算的方式，所以FPFH结合SPFH值，重新捕获邻近重要点对的几何信息；由于大大地降低了FPFH的整体复杂性，因此FPFH有可能使用在实时应用中；在FPFH中，通过分解三元组（三个角特征）简化了合成的直方图，即简单地创建b个相关的的特征直方图，每个特征维数（dimension）对应一个直方图（bin），并将它们连接在一起。pcl默认，in PFH assume the number of quantum bins (i.e. subdivision intervals in a feature’s value range),bins（b）=5即子区间数量，三个角特征元素，3^5=125,也就是一个查询点就有125个子区间，PFHSignature125的由来。这样有一个问题：对于点云特别是稀疏点云来说，很多区间存在0值，即直方图上存在冗余空间。因此，在FPFH中，通过分解三元组（三个角特征）简化了合成的直方图，即简单地创建b个不相关的的特征直方图，每个特征维数（dimension）对应一个直方图（bin），并将它们连接在一起。pcl默认FPFH的b=11，3*11=33，也就是FPFHSignature33的由来。
2.3 PCL实现
/** \brief 根据(f1, f2, f3)三个特征值计算单个SPFH
* \param[in] cloud 输入点云
* \param[in] normals 法线信息
* \param[in] p_idx 查询点(source)
* \param[in] row 在特征直方图里对应的行号
* \param[in] indices k近邻索引
* \param[out] hist_f1 f1特征矩阵
* \param[out] hist_f2 f2特征矩阵
* \param[out] hist_f3 f3特征矩阵
*/
template void
pcl::FPFHEstimation::computePointSPFHSignature (
const pcl::PointCloud &cloud, const pcl::PointCloud &normals,
int p_idx, int row, const std::vector &indices,
Eigen::MatrixXf &hist_f1, Eigen::MatrixXf &hist_f2, Eigen::MatrixXf &hist_f3)
{
Eigen::Vector4f pfh_tuple;
// 从直方图矩阵中获取特征的分隔数bins
int nr_bins_f1 = static_cast (hist_f1.cols ());
int nr_bins_f2 = static_cast (hist_f2.cols ());
int nr_bins_f3 = static_cast (hist_f3.cols ());
// Factorization constant
float hist_incr = 100.0f / static_cast(indices.size () - 1);
// 对近邻点进行迭代计算
for (size_t idx = 0; idx
assert (indices.size () == dists.size ());
double sum_f1 = 0.0, sum_f2 = 0.0, sum_f3 = 0.0; // 各特征值的总和
float weight = 0.0, val_f1, val_f2, val_f3; // 权值和
// 获取特征分隔数bins
int nr_bins_f1 = static_cast (hist_f1.cols ());
int nr_bins_f2 = static_cast (hist_f2.cols ());
int nr_bins_f3 = static_cast (hist_f3.cols ());
int nr_bins_f12 = nr_bins_f1 + nr_bins_f2;
// 清空直方图，这里共33个
fpfh_histogram.setZero (nr_bins_f1 + nr_bins_f2 + nr_bins_f3);
// Use the entire patch
for (size_t idx = 0, data_size = indices.size (); idx
val_f1 = hist_f1 (indices[idx], f1_i) * weight;
sum_f1 += val_f1;
fpfh_histogram[f1_i] += val_f1;
}
for (int f2_i = 0; f2_i
val_f3 = hist_f3 (indices[idx], f3_i) * weight;
sum_f3 += val_f3;
fpfh_histogram[f3_i + nr_bins_f12] += val_f3;
}
}
if (sum_f1 != 0)
sum_f1 = 100.0 / sum_f1; // histogram values sum up to 100
if (sum_f2 != 0)
sum_f2 = 100.0 / sum_f2; // histogram values sum up to 100
if (sum_f3 != 0)
sum_f3 = 100.0 / sum_f3; // histogram values sum up to 100
// 调整最终的FPFH值，乘了100
for (int f1_i = 0; f1_i
// 对每个近邻进行迭代计算
for (size_t idx = 0; idx size (); ++idx)
{
// 找到每个近邻的k近邻
if (this->searchForNeighbors((*indices_)[idx], search_parameter_, nn_indices, nn_dists) == 0)
{
// 如果某一近邻的近邻查找失败，则输出点云非dense，FPFH置为NaN
for (int d = 0; d points
for (size_t i = 0; i
if (!isFinite ((*input_)[(*indices_)[idx]]) ||
this->searchForNeighbors ((*indices_)[idx], search_parameter_, nn_indices, nn_dists) == 0)
{
for (int d = 0; d points
for (size_t i = 0; i |
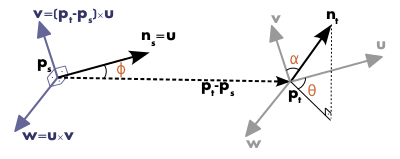
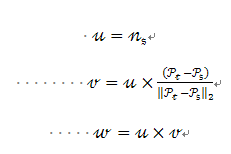使用上图中uvw坐标系，法线Ni和Nj之间的偏差可以用一组角度来表示，如下所示： 
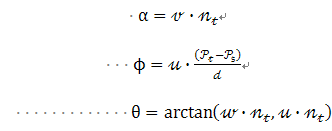d是两点Ps和Pt之间的欧氏距离 
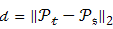计算k邻域内的每一对点的 
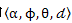四组值，这样就把两点和它们法线相关的12个参数（xyz坐标值和法线信息）减少到4个。 为每一对点估计PFH四元组，可以使用：
【本文地址】