最小二乘支持向量机分类器（LSSVM）及Python实现

在这篇文章中，我们讨论支持向量机(SVM)分类器的最小二乘版本。由于公式中的相等类型约束。解是由解一组线性方程得出的。而不是经典的支持向量机的二次规划。 本文针对两类分类问题，提出了支持向量机的最小二乘模型。对于函数估计问题，支持向量解释边缘回归。在(Saunders et al.， 1998)中，它考虑了等式类型的约束，而不是经典的支持向量机方法中的不等式。在这里，我们也考虑了在最小二乘意义下的公式分类问题的等式约束。因此，求解直接遵循求解一组线性方程，而不是二次规划。在经典的支持向量机中，许多支持值为零(非零值对应于支持向量)，而在最小二乘支持向量机中，支持值与误差成正比。

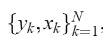给定N个点的训练集 ，Xk是第K个输入模式，Yk是第K个输出模式，支持向量机方法旨在构建一种分类器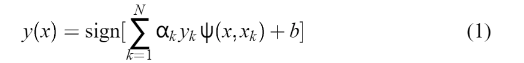： αk 是正常量，b是实常量，对于 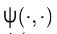有下列选择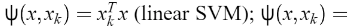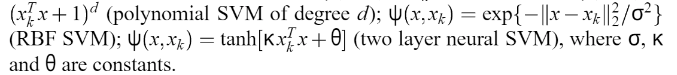： 构建如下分类器： 假定 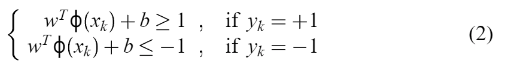这个式子等同于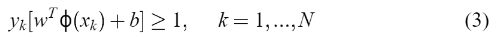 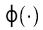是非线性函数，它映射输入空间到更高维空间。 然而，这个函数不是显式构造的。为了有违反(3)的可能性，在这个高维空间中不存在一个分离的超平面时，引入了这样的变量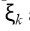 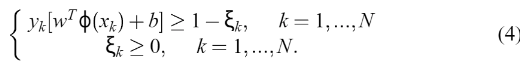根据结构风险最小化原则，将优化问题公式化，使风险界最小化: 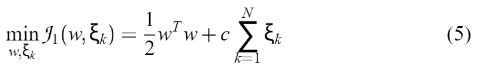它满足（4)。同时通过引入拉格朗日乘数 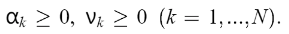，我们构建了拉格朗日方程 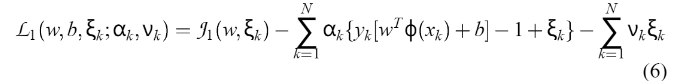通过计算 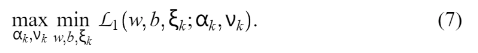获得拉格朗日点的解。 一个解是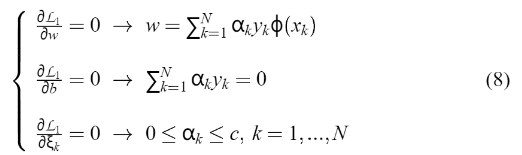： 它会影响下面这个二次规划问题的答案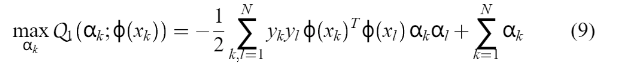： 比如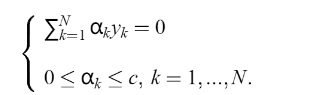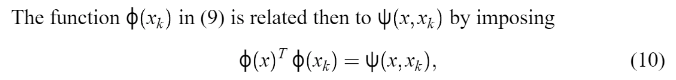： 这是由默瑟定理提出的。需要注意的是，对于两层神经支持向量机，Mercer‘s ’条件仅支持K和theta 的特定参数值。 通过解决 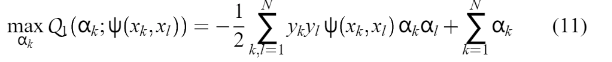设计分类器（1），它满足（9）中的条件。为了确定决定决策面，没有计算w和ф(x)。 因为矩阵与这个二次规划问题不是无限期的，(11)的解决方案将是全局的。 并且，超平面（3）满足 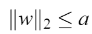，VC-维度h满足： [ . ]表示整数部分和r是包含点的半径最小的球中φ(x1)、…φ(xN)。通过定义拉格朗日函数就可以找到这个球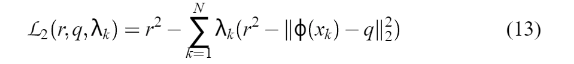

q表示球心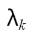， 是正拉格朗日变量。 与（5）中发现与 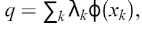等同的球心相似的方式，从 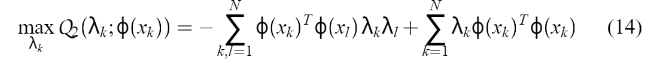找到拉格朗日变量，其中 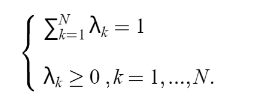根据(10)，Q2也可以表示为 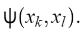最后，通过求解(11)并从(14)中计算(12)来选择一个VC维最小的支持向量机。

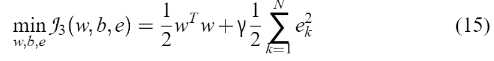（1）优化目标 这里我们将最小二乘版本引入SVM分类器，将分类问题表述为: 它满足平等的限制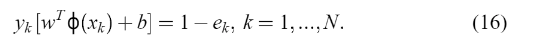： （2）拉格朗日乘子法

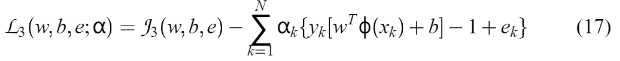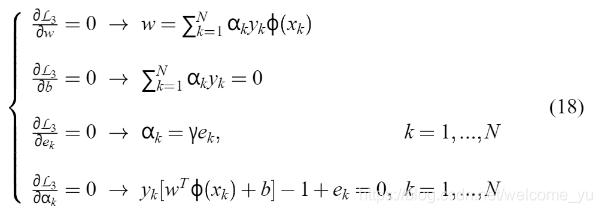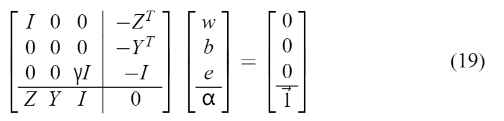
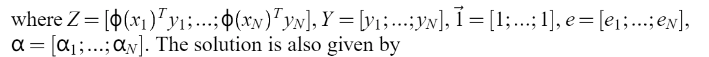
定义拉格朗日函数： 其中 aK 是拉格朗日乘数的等式约束，现在可以是正的或负的)。 （3）求解最优化条件 约束优化： （4）求解对偶问题 上式可以直接写成以下一组线性方程的解(Fletcher, 1987)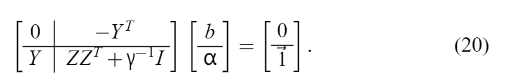： Mercer’s 的条件可以再次应用到矩阵 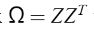其中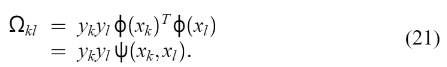， 因此，分类器(1)是通过求解线性方程组(20)(21)而不是二次规划得到的。如RBF核的σ等核的参数可根据(12)进行优化选择。支持值 αk 与数据点(18)的误差成比例，而在(14)的情况下，大多数值等于零。因此，在最小二乘情况下，人们更愿意说一个支持值谱。 LLSVM通过求解上述线性方程组，得到优化变量a aa和b bb的值，这种求解方式比求解QP问题更加简便。 最小二乘支持向量机求解时，计算成本低，并且没有许多局部最小值，是一个凸优化问题的解决方案。 并且泛化性能较好。 （5）与标准SVM的区别

a. 使用等式约束，而不是不等式约束； b. 由于对每个样本点采用了等式约束，因此对松弛向量不施加任何约束，这也是LSSVM丢失稀疏性的重要原因； c. 通过解决等式约束以及最小二乘问题，使得问题得到进一步简化。

特性： 1) 同样是对原始对偶问题进行求解，但是通过求解一个线性方程组（优化目标中的线性约束导致的）来代替SVM中的QP问题（简化求解过程），对于高维输入空间中的分类以及回归任务同样适用； 2) 实质上是求解线性矩阵方程的过程，与高斯过程（Gaussian processes），正则化网络（regularization networks）和费雪判别分析（Fisher discriminant analysis）的核版本相结合； 3) 使用了稀疏近似（用来克服使用该算法时的弊端）与稳健回归（稳健统计）； 4) 使用了贝叶斯推断（Bayesian inference）； 5) 可以拓展到非监督学习中：核主成分分析（kernel PCA）或密度聚类； 6) 可以拓展到递归神经网络中。 缺点： （1）解决分类任务时，全部训练样本都会被作为支持向量来看待，这就会导致其丧失SVM原有的稀疏性质，但是还可以通过对训练集进行基于支持度的“减枝”（pruning）处理来达到稀疏化的目的，这一步也可以看做是一种稀疏近似（sparse approximate）操作。 （2）

参考： 文章 源码 博客